Ôn thi tốt nghiệp THPT môn Toán theo câu - Câu III
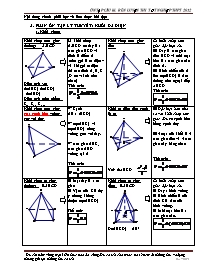
Khối chóp tam giác thường: A.BCD
Diện tích xq:
dt(ABC)+dt(ACD)
+dt(ABD)
Diện tích toàn phần:
Stp=Sxq+Sđáy Là khối chóp A.BCD có đáy là 1 tam giác BCD và đỉnh là điểm A
(còn gọi là tứ diện – và khi gọi tứ diện thì các đỉnh A, B, C ,D có vai trò như nhau)
Thể tích:
Bạn đang xem tài liệu "Ôn thi tốt nghiệp THPT môn Toán theo câu - Câu III", để tải tài liệu gốc về máy bạn click vào nút DOWNLOAD ở trên
Nội dung chính phải học và làm được bài tập: PHẦN ÔN TẬP LÝ THUYẾT: KHỐI ĐA DIỆN 1. Khối chóp: Khối chóp tam giác thường: A.BCD Diện tích xq: dt(ABC)+dt(ACD) +dt(ABD) Diện tích toàn phần: Stp=Sxq+Sđáy Là khối chóp A.BCD có đáy là 1 tam giác BCD và đỉnh là điểm A (còn gọi là tứ diện – và khi gọi tứ diện thì các đỉnh A, B, C ,D có vai trò như nhau) Thể tích: Khối chóp tam giác đều Là khối chóp tam giác đặc biệt có: J Đáy là tam giác đều BCD và mỗi mặt bên là 1 tam giác cân đỉnh A. J Hình chiếu của A lên mp(BCD) là tâm đường tròn ngoại tiếp DBCD Thể tích: Khối chóp tam giác có 1 cạnh bên vuông góc với đáy F Cạnh AB ^ (BCD) F mp(ABC) và mp(ABD) cùng vuông góc với đáy. F tam giác ABC, tam giác ABD vuông tại A Thể tích: Khối tứ diện đều cạnh là a: Với: dtDBCD = J Đặc biệt hơn nữa so với khối chóp tam giác đều có cạnh bên bằng cạnh đáy J 4 mặt của khối là 4 tam giác đều và 4 tam giác này bằng nhau Thể tích: Khối chóp tứ giác thường: S.ABCD J Mặt đáy là 1 tứ giác J Vị trí của S là tùy ý nhưng không thuộc mp(ABCD) Thể tích: Khối chóp tứ giác đều: S.ABCD H Dt(ABCD) = AB2 Là khối chóp tam giác đặc biệt có: J Đáy 1 hình vuông J Hình chiếu H của đỉnh S là tâm của hình vuông. J Mỗi mặt bên là 1 tam giác cân. Khối chóp tứ giác có 1 cạnh bên vuông góc với đáy ABCD: FCó: SA^(ABCD) F(SAB)^(ABCD) F(SAD)^(ABCD) FThể tích: V = .Bh Khối chóp tứ giác có 1 mặt bên vuông góc với đáy ABCD: J (SAD)^(ABCD) Nếu SH^AD thì: SH ^(ABCD) Nên SH là đường cao khối chóp Thể tích: 2. Khối chóp cụt: Khối chóp cụt: F Khối chóp cụt là phần của khối chóp tương ứng ở giữa mặt đáy và 1 thiết diện song song với đáy F Mỗi mặt bên là 1 hình thang Khối chóp cụt đều J Là khối chóp cụt có đáy là đa giác đều và đoạn nối tâm 2 đáy là chiều cao. J Mỗi mặt bên là 1 hình thang cân 3. Khối lăng trụ : Khối lăng trụ tam giác thường: ABC.A’B’C’ Diện tích xq: dt(AA’B’B)+dt(AA’C’C) +dt(BB’C’C) Diện tích toàn phần: Stp=Sxq+S2đáy F Có đáy là tam giác. F(ABC)//(A’B’C’) F AA’//BB’//CC’ F Mỗi mặt bên là 1 hình bình hành Thể tích: V = (dtDABC).h Khối lăng trụ tam giác đều: J Có đáy ABC, A’B’C’ là 2 tam giác đều nằm trong 2 mặt phẳng song song J Cạnh bên ^ đáy J Mỗi mặt bên là 1 hình chữ nhật Thể tích: V = dtDABC. AA’ Khối hộp F Là khối lăng trụ có đáy là hình bình hành F Có tất cả 6 mặt đều là 6 hình bình hành Thể tích: V = Bh=dt(ABCD).h Khối lăng trụ tứ giác đều: J Là 1 khối lăng trụ đứng(cạnh bên^đáy) J Có đáy là hình vuông (tứ giác đều) J Mỗi mặt bên là 1 hình chữ nhật Thể tích: V=dt(ABCD).AA’ Khối hộp chữ nhật: F Là khối lăng trụ đứng (có cạnh bên ^ đáy) F Tất cả 6 mặt đều là hình chữ nhật Thể tích: V = AB.AD.AA’ Khối lập phương: J Là 1 khối lăng trụ có 6 mặt là 6 hình vuông và 6 hình vuông này đều bằng nhau. J Là 1 khối lăng trụ đều có cạnh bên bằng cạnh đáy Thể tích: V = AB3 4. Khối trụ và khối nón: Khối nón: F Đỉnh S và mặt đáy là 1 hình tròn có tâm O là hình chiếu của đỉnh S F Diện tích xung quanh: F Thể tích Khối trụ: J Hai đáy là 2 hình tròn có tâm là O và O’ J Độ dài OO’ là chiều cao. F Diện tích xung quanh: F Thể tích Khối cầu: F Khối cầu tâm O là trung điểm của đường kính AB. Diện tích mặt cầu: Thể tích khối cầu: Xác định tâm mặt cầu Biết mặt cầu qua 3 điểm A,B,C Þ tâm mặt cầu nằm trên trục của DABC Xác định tâm mặt cầu Biết mặt cầu đi qua 2 điểm A và B thì tâm mặt cầu nằm trên mặt phẳng trung trực đoạn AB 5. Các công thức quan trọng khác: FHình vuông cạnh a có diện tích FHình chữ nhật có cạnh a,b có diện tích F Hình thoi biết hai đường chéo a,b FHình bình hành biết cạnh a và đường cao hA : FHình thang hai đáy a,b chiều cao h F Diện tích tam giác F Diện tích tam giác(tt) = ..... Hệ thức lượng trong tam giác vuông ABC vuông tại A. AH.BC = AB.AC (đối/huyền) (kề/huyền) (đối/kề) Trong tam giác ABC: Định lý cosin: Định lý sin: Tỉ số diện tích: Cho tam giác ABC và đường thẳng d cắt AB,AC lần lượt tại B’,C’ khi đó Tỉ số thể tích: Cho tứ diện S.ABC mặt phẳng (P) cắt các cạnh SA,SB,SC lần lượt tại A’B’C’ khi đó PHẦN BÀI TẬP MINH HỌA: Nội dung bài giải Phương pháp giải Bài tâp 1: Cho hình chóp S.ABCD có đáy ABCD là hình thang , AB=BC=a,AD = 2a, SA vuông góc với đáy và SA = 2a. Gọi M, N lần lượt là trung điểm của SA, SD. Tính thể tích khối chóp S.ABCD. Chứng minh rằng BCNM là hình chữ nhật và tính thể tích của khối chóp S.BCNM theo a. Giải: Đáy là hình thang có diện tích: = Vậy thể tích Ta có:MN // AD // AB ÞBMNC là hình bình hành (1) Mặt khác: BC ^ AB và BC ^ SA Þ BC ^ (SAB) Þ BC ^ BM ( vì BM Ì (SAB) ) (2) Từ (1), (2) Þ tứ giác BMNC là hình chữ nhật Þ VS.MCB = VS.ABC Mà: Suy ra: VS.MCB = = Tương tự: Mà: Suy ra: VS.MNC = Vậy VS.BMNC = VS.MBC + VS.MNC = + = Khối chóp S.ABCD có đáy là hình thang ABCD và đường cao là SA?? J Áp dụng công thức tính thể tích khối chóp diện tích đáy. Chiều cao J Sử dụng tính chất đường trung bình trong tam giác J BC ^ (SAB) nên BC vuông góc với mọi đường thẳng thuộc mp(SAB) Áp dụng các tỉ số thể tích trong từng khối chóp tam giác S.ABC và S.ADC Khi tính hay nên biết các tỉ số này chỉ sử dụng được cho khối chóp tam giác mà thôi Bài tập 2: Cho hình chóp S.ABC có SA^(ABC) đáy ABC là tam giác vuông tại B. Gọi H,K là hình chiếu của A lên SB,SC cho SA=AB=BC=a Tính thể tích khối chóp S.ABC. Chứng minh rằng SC^ AH. Giải: Dt(ABC) = ( DABC vuông tại B) thể tích khối chóp S.ABC: VS.ABC= dt(ABC).SA = .a = Ta có AH ^ SB AH ^ BC ( vì BC ^ AB, BC ^ SA Þ BC ^ (SAB) Þ AH ^ mp(SBC) Þ AH ^ SC Thể tích VS.ABC= 13dt(ABC).SA Bài tập 3: Cho lăng trụ tứ giác đều ABCD.A’B’C’D’có cạnh bên bằng 4a và đường chéo 5a. Tính thể tích khối lăng trụ này. Giải: Tam giác BDD’ vuông tại D nên: BD2 = BD’2 – DD’2 = = 9a2 Þ BD = 3a. Mà ABCD là hình vuông co đường chéo BD = 3a Þ AB = Vậy thể tích của khối lăng trụ ABCD.A’B’C’D’: VABCD.A’B’C’D’ = DT(ABCD).AA’ = .4a = 9a3. Bài tập 4: Xác định tâm và tính bán kính của mặt cầu nội tiếp tứ diện đều ABCD có cạnh là a. Giải: Gọi O là hình chiếu của D lên mp(ABC), O là trọng tâm của tam giác đều ABC. Mặt phẳng trung trực của đọan AD cắt AD tại E và cắt DO tại K. Ta có KD = KA = KB = KC nên K là tâm của mặt cầu nội tiếp tứ diên đều vì : d(K,(DAB)) = d(K, (DBC)) = d(K, (DAC)) = d(K, (ABC)) = OK Ta có : AO = , OD = Vì đồng dạng ta có : Vậy OK = OD – DK = . Ta cần tìm tâm K mặt cầu ngoại tiếp tứ diện ABCD K cách đều BCD Þ K thuộc trục của tam giác BCD Cách đều A và D Þ K thuộc đường trung trực đoạn AD trong mp(DAO) Bài tập 5: Đáy của lăng trụ đứng tam giác ABC.A’B’C’ là tam giác đều . Mặt (A’BC) tạo với đáy một góc 300 và diện tích tam giác A’BC bằng 8. Tính thể tích khối lăng trụ. Giải: Giả sử BI = x Ta có A’A = AI.tan 300 = Vậy VABC.A’B’C’ = CI.AI.A’A = x3 Mà SA’BC = BI.A’I = x.2x = 8 Do đó VABC.A’B’C’ = 8 BÀI TẬP RÈN LUYỆN Bài 1: Cho hình chóp đều SABC có cạnh bên bằng a và cạnh bên hợp với đáy ABC một góc 60o . Tính thể tích hình chóp. Đs: Bài 2: Cho hình chóp tam giác đều SABC có cạnh bên a, góc ở đáy của mặt bên là 45o. 1) Tính độ dài chiều cao SH của chóp SABC . Đs: SH = 2) Tính thể tích hình chóp SABC. Đs: Bài 3: Cho hình chóp tam giác đều SABC có cạnh đáy a và mặt bên hợp với đáy một góc 60o. Tính thể tích hình chóp SABC. Đs: Bài 4 : Cho hình chóp tứ giác đều SABCD có cạnh đáy a và . 1) Tính tổng diện tích các mặt bên của hình chóp đều. Đs: 2) Tính thể tích hình chóp. Đs: Bài 5: Cho hình chóp tứ giác đều S.ABCD có cạnh bên bằng a, cạnh bên hợp với đáy một góc 60o.Tính thề tích hình chóp. Đs: Bài 6: Cho hình chóp tứ giác đều S.ABCD có mặt bên hợp với đáy một góc 45o và khoảng cách từ chân đường cao của chóp đến mặt bên bằng a.Tính thể tích khối chóp . Đs: Bài 7: Cho lăng trụ đứng ABC A'B'C' có đáy ABC vuông cân tại B biết A'C = a và A'C hợp với mặt bên (AA'B'B) một góc 30o . Tính thể tích lăng trụ. ĐS: Bài 8: Cho lăng trụ đứng ABC A'B'C' có đáy ABC vuông tại B biết BB' = AB = a và B'C hợp với đáy (ABC) một góc 30o . Tính thể tích lăng trụ. ĐS: Bài 9: Cho lăng trụ đứng ABC A'B'C' có đáy ABC là tam giác đều cạnh a biết AB' hợp với mặt bên (BCC'B') một góc 30o . Tính độ dài AB' và thể tích lăng trụ . ĐS: ; Bài 10: Cho lăng trụ đứng ABC A'B'C' có đáy ABC vuông tại A biết AC = a và ACB=60o biết BC' hợp với mặt bên (AA'C'C) một góc 30o . Tính thể tích lăng trụ và diện tích tam giác ABC'. ĐS: , S = Bài 11: Cho lăng trụ tam giác đều ABC A'B'C' có khoảng cách từ A đến mặt phẳng (A'BC) bằng a và AA' hợp với mặt phẳng (A'BC) một góc 300 . Tính thể tích lăng trụ ĐS: Bài 12: Cho tứ diên ABCD. Gọi B' và C' lần lượt là trung điểm của AB và AC. Tính tỉ số thể tích của khối tứ diện AB'C'D và khối tứ diên ABCD. Đs: Bài 13: Cho tứ diên ABCD có thể tích 9a3 ,trên AB,AC,AD lần lượt lấy các điểm B',C',D' sao cho AB = 2AB' ;2AC = 3AD' ;AD = 3AD'. Tính tể tích tứ diện AB'C'D'. Đs: V = 2a3 Bài 14: Cho tứ diên đều ABCD có cạnh a. Lấy các điểm B';C' trên AB và AC sao cho . Tính thể tích tứ diên AB'C'D . Đs: Bài 15: Cho hình chóp SABC có đáy ABC là tam giác đều cạnh ,đường cao SA = a.Mặt phẳng qua A và vuông góc với SB tại H và cắt SC tại K. Tính thể tích hình chóp SAHK. Đs: Bài16: Cho lăng trụ đứng ABC.A’B’C’ có đáy là tam giác vuông cân tại B, AC = 2a.Góc giữa A’B và (ABC) là 600. Gọi M,N lần lượt là trung điểm A’B và A’C. Tính thể tích khối A.BCNM. Bài 17: Cho lăng trụ đứng ABC.A’B’C’ có đáy là tam giác đều cạnh a.Góc giữa (A’BC) và (ABC) là 600. Gọi K lần lượt là trung điểm A’B và H là hình chiếu của A lên A’C. Tính thể tích khối A.BCKH Bài 18: Thiết diện qua trục của hình trụ là một hình vuông cạnh 2a Tính thể tích và diện tích xung quanh khối trụ theo a. Đs: Sxq=4pa2, V = 2pa3 Tính thể tích khối lăng trụ tứ giác đều nội tiếp khối trụ Đs: V = 4a3 Bài 19: Một hình nón có đường sinh bằng a góc ở đỉnh bằng 900. Cẳt hình nón bởi một mặt phẳng (P) đi qua đỉnh sao cho góc giữa (P) và đáy hình nón bằng 600. Tính thể tích và diện tích toàn phần của khối nón. Đs: V=;Stp= Tính diện tích thiết diện. Đs: S =
Tài liệu đính kèm:
 CAU III - TOT NGHIEP THPT 2012.doc
CAU III - TOT NGHIEP THPT 2012.doc





