Ôn tập tốt nghiệp Hình học 12
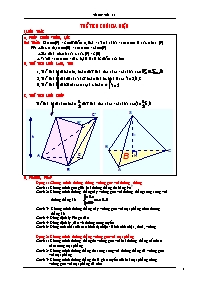
A. PHÉP CHIẾU VUÔNG GÓC
BÀI TOÁN: Cho mp(P) và một điểm A. Hãy vẽ hình chiếu vuông góc H của A trên (P)
PP: + Qua A dựng mp(Q) vuông góc với mp(P)
+ Xác định giao tuyến a của (P) và (Q)
+ Vẽ AH vuông góc vối a tại H thì H là điểm cần tìm
Bạn đang xem tài liệu "Ôn tập tốt nghiệp Hình học 12", để tải tài liệu gốc về máy bạn click vào nút DOWNLOAD ở trên
THỂ TÍCH KHỐI ĐA DIỆN I.KIẾN THỨC A. PHÉP CHIẾU VUÔNG GÓC BÀI TOÁN: Cho mp(P) và một điểm A. Hãy vẽ hình chiếu vuông góc H của A trên (P) PP: + Qua A dựng mp(Q) vuông góc với mp(P) + Xác định giao tuyến a của (P) và (Q) + Vẽ AH vuông góc vối a tại H thì H là điểm cần tìm B. THỂ TÍCH KHỐI LĂNG TRỤ 1. Thể tích khối lăng trụ bằng diện tích đáy nhân với chiều cao 2. Thể tích khối hộp chữ nhật bằng tích ba kích thước V=a.b.c 3. Thể tích khối lập phương cạnh a bằng a3 : V=a3 C. THỂ TÍCH KHỐI CHÓP Thể tích khối chóp bằng diện tích đáy nhân với chiều cao.V=S.h II. PHƯƠNG PHÁP Dạng 1: Chứng minh đường thẳng vuơng gĩc với đường thẳng Cách 1: Chứng minh gĩc giửa hai dường thẳng đĩ bằng 900 Cách 2: Chứng minh dường thẳng này vuơng gĩc với đường thẳng song song với đường thẳng kia Cách 3: Chứng minh đường thẳng này vuơng gĩc với mặt phẳng chứa đướng thẳng kia Cách 4: Dùng định lý Pitago đảo Cách 5: Dùng định lý đảo về đường trung tuyến Cách 6: Dùng tính chất của các hình đặc biệt : Hình chữ nhật , thoi , vuơng Dạng 2: Chứng minh đường thẳng vuơng gĩc với mặt phẳng Cách 1: Chứng minh đường thẳng đĩ vuơng gĩc với hai đường thẳng cắt nhau nằm trong mặt phẳng Cách 2: Chứng minh đường thẳng đĩ song song với đường thẳng đã vuơng gĩc với mặt phẳng Cách 3: Chứng minh đường thẳng đĩ là giao tuyến của hai mặt phẳng cùng vuơng gĩc với mặt phẳng đã cho Cách 4: Chứng minh đường thẳng đĩ vuơng gĩc với mặt phẳng song song với mặt phẳng đã cho Cách 5: Chứng minh đường thẳng đĩ nằm trong mặt phẳng vuơng gĩc với mặt phẳng đã cho và vuơng gĩc với giao tuyến của hai mặt phẳng đĩ Dạng 3: Chứng minh hai mặt phẳng vuơng gĩc Cách 1:Chứng minh trong mặt phẳng này cĩ chứa một đường thẳng vuơng gĩc với mặt phẳng kia Cách 2: Chứng minh mặt phẳng này song song với đường thẳng vuơng gĩc với mặt phẳng ki Dạng 4:Xác định khoảng cách từ một điểm A đến đường thẳng a Cách tìm: Tìm một mặt phẳng (P) chứa điểm A và vương gĩc với a Tìm giao điểm H của (P) và a . Khoảng cách là AH. Dạng 5: Xác định khoảng cách từ điểm M đến mặt phẳng (P) Cách tìm : Tìm mặt phẳng (P) chứa M và vuơng gĩc với mặt phẳng đã cho Tìm giao tuyến a của (P) và mặt phẳng đã cho Kẻ MH vuơng gĩc với a tại H . Khoảng cách là MH Dạng 6: Xác định khoảng cách giữa hai đường thẳng chéo nhau a và b Cách giải: Tìm mặt phẳng (P) chứa a và song song b . Khoảng cách giữa a và b là khoảng cách từ b đến (P) Chú ý: Nếu a và b vuơng gĩc nhau. Tìm mặt phẳng (P) chứa a và vuơng gĩc với b tại B Trong (P) kẻ BA a tại A. Thì AB là khoảng cách Dạng 7: Xác định gĩc giữa hai đường thẳng a và b Cách giải: Tìm hai đường thẳng a’ và b’ cắt nhau và lần lựot song song với a và b Gĩc giữa a và b là gĩc giữa a’ và b’ Chú ý: Gĩc giữa hai đường thẳng cĩ số đo khơng lớn hơn 900 Dạng 8: Xác định gĩc giữa đường thẳng a và mặt phẳng Cách giải: Tìm hình chiếu a’ của a trên mặt phẳng .Gĩc giữa a và là gĩc giữa a và a’ Chú ý: Gĩc giữa đường thẳng và mặt phẳng cĩ số đo khơng quá 900 Dạng 9: Xác định gĩc giữa hai mặt phẳng và Cách giải: Tìm giao tuyến của hai mặt phẳng đĩ Trong tìm đường thẳng a , trong tìm đường thẳng b sao cho a và b cùng vuơng gĩc với tai O .Thì gĩc giữa hai mặt phẳng là gĩc giữa a và b Dạng 10 : Tính thể tích hình chĩp, lăng trụ, khối nĩn, khối trụ Cách giải : Dùng cơng thức . Thể tích hình lăng trụ , hình trụ bằng diện tích đáy nhân với chiều cao Thể tích hính chĩp , hình nĩn thì bằng 1/3 diện tích nhân với chiều cao. Dạng 11 Tính diện tích xung quanh, diên tích tồn phần Cách giải: Dùng cơng thức Diện tích xung quanh bằng tổng diện tích các mặt bên Diện tích tồn phần bằng diện tích xung quanh cộng diện tích các đáy Chú ý: Diện tích xung quanh của hình chĩp đều thì bằng chu vi đáy nhân với trung đoạn III. BÀI TOÁN Bài 1./ Cho hình chóp S.ABC có SA=SB=SC=a và thỏa a). CMR: Tam giác ABC vuông b). Hạ SH vuông góc mp(ABC). Xác định vị trí của H c). Tính đoạn SH. Bài 2./ Cho tứ diện SABC có SA, SB, SC đôi một vuông góc nhau, SA=a, SB=b, SC=c. Hạ SH vuông góc mp(ABC). a). CMR: H là trực tâm của tam giác ABC b). Tính đoạn SH Bài 3./ Cho lăng trụ đứng ABCA’B’C’, có đáy là tam giác ABC vuông tại A, AC=a, . Biết BC’ tạo với (ACC’A’) một góc là 300. a). Tính AC’ b). Tính thể tích khối lăng trụ. Bài 4: Cho khối lăng trụ ABCA’B’C’ có đáy lam giác ABC vuông cân tại A. Mặt bên (ABB’A’) là hình thoi cạnh A và vuông góc với (ABC), còn mặt bên (ACC’A’) tạo với đáy một góc 300.Tính thể tích khối lăng trụ Bài 5: Cho hình chóp S.ABC là hình chóp tam giác đều có cạnh đáy AB=a, cạnh bên SA=b. Tính thể tích khối chóp Bài 6: Cho hình chóp tam giác đều S.ABC cạnh bên SA=a, mặt bên tạo với đáy một góc 450 Tính thể tích khối chóp Bài 7: Cho hình chóp tứ giác đều S.ABCD có cạnh đáy AB=a, cạnh bên tạo với đáy một góc 450 .Tính thể tích khối chóp. Bài 8: Cho khối hộp ABCD.A’B’C’D’ có thể tích là V. Tính thể tích của tứ diện ACB’D’ theo V. Bài 9: Cho hình chóp S.ABC, đáy là tam giác ABC đều cạnh a, (SAB)(ABC) và hai mặt bên còn lại cùng tạo với đáy một góc 450 . Tính thể tích khối chóp. Bài 10: Cho hình chóp tứ giác đều S.ABCD, cạnh đáy AB=a và mặt bên có diện tích bằng diện tích mặt đáy. a). Tính thể tích khối chóp b). Cho M là điểm bất kỳ ở trong hình chóp. Chứng minh rằng tổng các khoảng cách từ M tới các mặt của hình chóp không phụ thuộc vào vị trí của M. MẶT NÓN ĐỊNH NGHĨA: Mặt nón: Hình nón, khối nón * Khối nón là phần không gian giới hạn bởi hình nón và kể cả hình nón đó. Diện tích hình nón thể tích khối nón Bài tập HÌNH TRỤ 1.MẶT TRỤ 2.HÌNH TRỤ 3. KHỐI TRỤ 4. BÀI TẬP MẶT CẦU 1.ĐỊNH NGHĨA 2.TÍNH CHẤT: 3. VỊ TRÍ CỦA MẶT CẦU VÀ MẶT PHẲNG 4. VỊ TRÍ GIỮA MẶT CẦU VÀ ĐƯỜNG THẲNG. Tính chất. 5. BÀI TẬP Ví dụ BIỂU THỨC TOẠ ĐỘ CỦA CÁC PHÉP TỐN VECTƠ : Trong khơng gian Oxyz cho hai vectơ và một số k , ta cĩ . 4. và cùng phương cĩ một số k sao cho hay 5. Nếu thì • . • Toạ độ trung điểm M của đoạn thẳng AB là : BIỂU THỨC TOẠ ĐỘ CỦA TÍCH VƠ HƯỚNG VÀ CÁC ỨNG DỤNG : a) Trong khơng gian Oxyz cho hai vectơ . Ta c ĩ : . b) Độ dài của một vectơ : Cho vectơ , ta c ĩ . c) Khoảng cách giữa hai điểm là d) Gọi là gĩc giữa hai vectơ . Ta cĩ : Và PHƯƠNG PHÁP GIẢI TỐN Dạng 1 Chứng minh ba điểm A , B, C thẳng hàng Cách giải: Chứng minh hai vectơ cùng phương. Dạng 2: Chứng minh 4 điểm A, B ,C , D đồng phẳng Cách giải: Chứng minh 3 vectơ đồng phẳng BÀI TẬP Bài 1: Cho ba điểm A ( 1 ; 0 ;-2 ) , B ( 2 ; 1 ;- 1 ) , C ( 1 ; -2 ; 2 ) . a) Chứng minh rằng A , B , C là ba đỉnh của tam giác . b) Tính chu vi của tam giác ABC. c) Tìm toạ độ trung điểm I của cạnh BC. d) Tìm toạ độ trọng tâm G của tam giác ABC. e) Tìm toạ độ điểm D sao cho tứ giác ABCD là hình bình hành. f) Tính gĩc BAC. Bài 2: Cho hình hộp ABCD.A’B’C’D’ ,biết A (1; 0 ; 1 ) , B ( 2 ; 1 ; 2 ) , D ( 1; -1 ; 1 ) và C’(4 ;5 ; -5 ) . Tìm toạ độ của các đỉnh cịn lại ? Bài 3: a) Tìm điểm M thuộc y’Oy sao cho M cách đều A ( 3 ; 1 ;0 ) và B ( -2 ; 4;1 ). b) Tìm điểm N thuộc mặt phẳng (Oxy) sao cho N cách đều A ( 1; 1 ;1 ) ,B ( -1 ;1 ; 0 ) và C ( 3 ; 1 ; -1 ) . Bài 4: Bài 5: Bài 6: Bài 7: MẶT CẦU + Phương trình mặt cầu cĩ dạng: PHƯƠNG PHÁP GIẢI TỐN Dạng 1: Xác định tâm và tính bán kính của mặt cầu Cách giải: + Nếu mặt cầu (S) cĩ dạng : (x – a )2 + (y – b )2 +( z – c )2 = R2 (1) Thì tâm là I( a , b , c ) ; bán kính là R + Nếu mặt cầu (S)cĩ dạng: x2 + y2 + z2 - 2ax – 2by - 2cz + d = 0 (2) Thì tâm I(a , b ,c); Bán kính Dạng 2: Lập phương trình mặt cầu Cách 1 + Tìm tâm I(a,b.c) và tính bán kính R + Phương trình mặt cầu là (S):(x – a )2 + (y – b )2 +( z – c )2 = R2 Cách 2 + Gọi (S) cĩ dạng x2 + y2 +z2 – 2ax – 2by -2cz + d = 0 (*) + Từ giả thiết lập một hê gồm 4 phương trình 4 ẩn a ,b , c , d + Giải hệ tìm a ,b ,c ,d . Thay vào (*) ta được kết quả. Dạng 3: Lập phương trình tiếp diện của mặt cầu (S). Cách giải + Tìm toạ độ tâm I (a,b,c) và tính bán kinh R của (S) + Viết phương trình tiếp diện (P) dạng : Ax + By + Cz + D = 0 (*) + Dùng điều kiện :(P) tiếp xúc (S) + Giải tìm các hệ số chưa cĩ . Thay vào (*). Dạng 4 Xác định vị trí tưong đối của mặt phẳng (P) và mặt cầ (S) Cách giải: + Tìm tâm I(a,b,c) và bán kính R của (S) + Tính d(I, (P) ) Nếu d > R : (P) khơng cắt (S) Nếu d = R : (P) tiếp xúc (S) Nếu d < R : (P) cắt (S) theo thiết diện là một đường trịn cĩ pt Dạng 5: Tìm tâm và bán kính của đường trịn giao tuyến của mặt phẳng và mặt cầu Cách giải + Tìm tâm I(a,b,c) và bán kính R của mặt cầu (S) + Tâm H của đường trịn là hình chiếu của I trên (P). + Bán kính đường trịn là r = BÀI TẬP: Bài 1: Viết phương trình mặt cầu (S) biết rằng : a) (S) cĩ tâm I ( -1 ; 2 ;3 ) và qua điểm A ( -2 ; 1 ; 1 ) . b) (S) cĩ đường kính AB với A ( 6 ; 2 ;-5 ) và B ( -4 ; 0 ; 7 ) . c) (S) cĩ tâm I ( 1 ; 4 ; -7 ) và tiếp xúc với mặt phẳng :. Bài 2: Lập phương trình mặt cầu (S) qua bốn điểm A ( 1 ; 1 ;0 ) , B ( 3 ; 1 ;2 ) , C ( -1 ; 1 ;2) D ( 1 ; -1 ;2 ) .Xác định tâm và bán kính của mặt cầu đĩ Bài 3: Lập phương trình mặt cầu (S) qua ba đi ểm A ( -2 ; 4 ;1 ) , B ( 3 ; 1 ;-3 ) ,C ( -5 ;0 ;0 ) và cĩ t âm nằm trên mặt phẳng : (P) : 2x + y – z + 3 = 0 . Bài 4: Bài 5: MẶT PHẲNG Phương trình mặt phẳng: 1. Phương trình mpqua M(x0;y0z0) cĩ vecto pháp tuyến là: A(x-x0)+B(y-y0)+C(z-z0)=0 Nếu hai vectơ khơng cùng phương, cĩ giá nằm trên mp hay song song với mp thì VTPT của mp là 2. Phương trình Ax+By+Cz+D=0 với là phương trình mặt phẳng cĩ vecto pháp tuyến 3. Mpcắt các trục toạ độ tại A(a;0;0),B(0;b;0),C(0;0;c) thì phương trình của là : 4. Cho : Ax+By+Cz+D=0 qua O song song hay chứa trục Ox song song hay trùng mp(Oxy) Các trường hợp cịn lại tương tự. Vị trí tương đối của hai mặt phẳng: Cho : Ax+By+Cz+D=0 : A’x+B’y+C’z+D’=0 vàcắt nhau vàsong song vàtrùng nhau và vuơng gĩc nhau Khoảng cách: 1. Khoảng cách từ một điểm đến mặt phẳng: Cho : Ax+By+Cz+D=0. Khoảng cách từ điểm M đến mp là IV. Gĩc giữa hai mặt phẳng: Cho 2 mặt phẳngvà cĩ VTPT là và PHƯƠNG PHÁP GIẢI TỐN Dạng 1: Lập phương trình mặt phẳng (P) Cách giải: + Tìm một điểm M(x0 , y0 , z0 ) và một VTPT của (P) + Phương trình của (P) là A(x – x0) + B( y – y0) + C( z – z0) = 0 Chú ý: Để tìm VTPT của (P) ta cĩ thể dùng một trong các trường hợp sau: + Mặt phẳng (P) cĩ cặp VTCP là thì VTPT của (P) là + Hai mặt phẳng song song thì cĩ VTPT bằng nhau + Hai mặt phẳng vuơng gĩc nhau thì các VTPT của chúng vuơng gĩc nhau + Mặt phẳng vuơng gĩc với đường thẳng thì VTPT của (P) là VTCP của đường thẳng. + Mặt phẳng đi qua 3 điểm A(a,0,0), B(0,b,0), C(0,0,c) cĩ pt là : + Pt (Oxy) là z = 0 ; Pt (Oxz) là y = 0 ; pt(Oyz) là x = 0. Dạng 2: Xét vị trí tương đối của hai mặt phẳng (P) : Ax +By +Cz +D = 0 , (Q) : A’x + B’y +C’z +D’= 0 Cách giải: + (P) cắt (Q) (VTPT (P), (Q) khơng cùng phương) BÀI TẬP 1./ 2./ 3./ 4./ 5./ 6./ 7/ 8./ 9./ 10./ 11./ 12./ 13./ 14./ 15./ 16./ 17./ 18./ 19./ 20,/ ĐƯỜNG THẲNG I. Phương trình đường thẳng: Cho đường thẳng (d) qua M(x0;y0z0) cĩ vecto chỉ phương Phương trình tham số của (d) là: Phương trình chính tắc của (d) là: II.Vị trí tương đối của hai đường thẳng: Cho (d) qua A cĩ VTCP (d’) qua B cĩ VTCP d cắt d’ d // d’ dd’ đơi một cùng phương d, d’ chéo nhau Khoảng cách: 1. Khoảng cách từ một điểm đến đường thẳng ( CT nâng cao) Cho () qua A cĩ VTCP , 2. Khoảng cách giữa hai đường thẳng chéo nhau (CT nâng cao) Cho () qua A cĩ VTCP , () qua B cĩ VTCP IV. Gĩc ( CT nâng cao) 1. Gĩc giửa hai đường thẳng: Cho 2 đường thẳngvà cĩ VTCP là và , 2. Gĩc giửa hai mặt phẳng: Cho 2 mặt phẳngvà cĩ VTPT là và , 3. Gĩc giửa đường thẳng và mặt phẳng: Cho () qua A cĩ VTCP , Mp() cĩ VTPT PHƯƠNG PHÁP GIẢI TỐN Dạng 1: Viết phương trình đường thẳng Cách giải: + Tìm một điểm M(x0 , y0 , x0 ) và một VTCP + Phương trình tham số là : + Phương trình chính tắc là : Dạng 2: Viết phương trình đường thẳng (d) đi qua điểm M và vuơng gĩc với 2 đường thẳng (d’) và (d’’) Cách giải: + Tìm VTCP của (d’) và (d”) + (d) là đường thẳng đi qua M và cĩ VTCP là : Dạng 3: Viết phương trình đường vuơng gĩc chung của 2 đường thẳng chéo nhau.(d) và (d’) Cách giải: + Tìm các VTCP của (d) ,(d’) : + Viết pt tham số của (d) , (d’) + Gọi M , M’là 2 điểm lần lượt thuộc (d) , (d’). Toạ độ M , M’ tính theo tham số t , t’ + MM’ là đường vuơng gĩc chung .Giải hệ tìm t và t’ + Đường thẳng vuơng gĩc chung là đường thẳng MM’ Dạng 4: Viết pt đường thẳng (d) đi qua M vuơng gĩc và cắt đường thẳng (d1) Cách giải: + Tìm toạ độ điểm M’ là hình chiếu vuơng gĩc của M trên (d1) + Đường thẳng (d) chính là đường thẳng MM’. Dạng 5: Tìm toạ độ M’ hình chiếu của M trên mp(P) Cách giải + Lập phương trình đường thẳng (d) đi qua M và vuơng gĩc mp(P) + Giải hệ phương trình ta được toạ độ điểm M’ Dạng 6: Tìm toạ độ M’ hình chiếu của M trên đường thẳng (d). Cách giải + Lập phương trình mp(P) đi qua M và vuơng gĩc với (P) + Toạ độ của M’ là nghiệm của hệ Dạng 7 Tìm toạ độ điểm M’ đối xứng M qua mp(P) Cách giải + Tìm toạ độ điểm H là hình chiếu của M trên (P) + M’ đối xứng với M qua (P) H là trung điểm của MM’ + M’(xm,ym) là điểm phải tìm Dạng 8: Tìm toạ độ điểm M’ đối xứng với điểm M qua đ/ thẳng (d). Cách giải + Tìm toạ độ điểm H là hình chiếu của M trên (d) + M’ đối xứng M qua (d) H là trung điểm MM’ Dạng 9: Các cơng thức tính gĩc . 1.Gĩc giữa hai đường thẳng (d), (d’): + Ttìm 2 VTCP của (d), (d’) : + 2.Gĩc giữa đường thẳng (d) và mặt phẳng(P) + Tìm + () 3.Gĩc giữa hai mặt phẳng (P) và (Q): + Tìm các VTPT của (P) và (Q) : + Dạng 10: Các cơng thức tính khoảng cách 1. Khoảng cách từ một điểm M0(x0,y0) đến mặt phẳng (P) : Ax+By+Cz + D = 0 + 2. Khoảng cách từ điểm M đến đường thẳng qua M0 cĩ VTCP . + Khoảng cách giữa hai đường thẳng chéo nhau:đi qua M0 cĩ VTCP ; đi qua cĩ VTCP + d BÀI TẬP 1. Trong kgOxyz, cho mp Tìm hình chiếu H của điểm M(-1;0;1) lên mp. Suy ra điểm M’ đối xứng của M qua mp Mp( cắt các trục toạ độ tại A,B,C.Tính thể tích tứ diện OABC. 2. Trong kgOxyz, cho a)Tìm hình chiếu H của điểm A(1;-1;0) lên Suy ra điểm A’ đối xứng của A qua đường thẳng CMR : và (d): là hai đường thẳng chéo nhau. 3. Trong kgOxyz, cho và CMR: (d) song song với mp Tính khoảng cách giửa (d) và mp 4. Trong kgOxyz, cho và CMR: cắt nhau.Tìm giao điểm I của chúng. b).Lập phương trình mp chứa và 5. Trong kgOxyz, cho CMR: Viết phương trình tham số của đường thẳng (D) là giao tuyến của hai mặt phẳng trên. 6. Trong kgOxyz, cho A(2;0;-2),B(1;-2;3) và Viết phương trình chính tắc của đường thẳng AB. Tìm giao điểm của đường thằng AB và mp Lập phương trình mp qua AB và vuơng gĩc với mp 7. Trong kgOxyz, cho A(4;0;1),B(2;-1;0),C(0;6;1),D(6;3;-2). Viết phương trình mp(BCD), suy ra ABCD là một tứ diện. Lập phương trình đường thẳng (D) qua trọng tâm G của tam giác BCD và vuơng gĩc với mp(BCD) 8. Trong kgOxyz, cho và CMR: và vuơng gĩc nhau và khơng cĩ điểm chung. Lập phương trình mp chứa và vuơng gĩc với 9. Trong kgOxyz, cho và (D): CMR : Hai đường thẳng trên song song nhau. Lập phương trình mặt phẳng chứa hai đường thẳng trên. Tài liệu này có sử dụng một số tư liệu của đồng nghiệp. Chỉ lưu hành nội bộ Tài liệu này có sử dụng một số tư liệu của đồng nghiệp.Chỉ lưu hành nội bộ
Tài liệu đính kèm:
 ON TAP TN HH.doc
ON TAP TN HH.doc





