Một số bài toán ôn tập có hướng dẫn giải
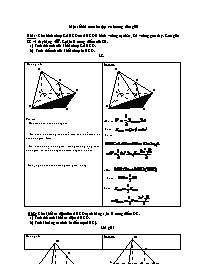
Bài 1: Cho hình chóp S.ABCD có ABCD là hình vuông cạnh 2a, SA vuông góc đáy. Góc giữa SC và đáy bằng . Gọi M là trung điểm của SB.
a) Tính thể tích của khối chóp S.ABCD.
b) Tính thể tích của khối chóp MBCD.
Bạn đang xem tài liệu "Một số bài toán ôn tập có hướng dẫn giải", để tải tài liệu gốc về máy bạn click vào nút DOWNLOAD ở trên
Một số bài toán ôn tập có hướng dẫn giải Bài 1: Cho hình chóp S.ABCD có ABCD là hình vuông cạnh 2a, SA vuông góc đáy. Góc giữa SC và đáy bằng . Gọi M là trung điểm của SB. Tính thể tích của khối chóp S.ABCD. Tính thể tích của khối chóp MBCD. LG Hướng dẫn Yêu cầu: + Học sinh xác định được góc. + Xác định được công thức thể tích của khối, tính độ dài đường cao SA. +Xác định được đường cao trong trường hợp chân đường cao có thể không thuộc mặt đáy của khối. +Sử dụng được hệ thức trong tam giác vuông Lời giải: a)Ta có Ta có : Ta có: b) Kẻ Ta có: , Ta có : Bài 2: Cho khối tứ diện đều ABCD cạnh bằng a, M là trung điểm DC. Tính thể tích khối tứ diện ABCD. Tính khoảng cách từ M đến mp(ABC). Lời giải Hướng dẫn Yêu cầu: + Học sinh nắm cách vẽ khối tứ diện đều và tính chất đặc biệt của khối. +Xác định được đường cao và ghi thể tích của khối +Sử dụng được định lý Pitago Lời giải: a) Gọi O là tâm của Ta có : Ta có: , Ta có: OC = 23CI=23.a.32=a33 b) Kẻ MH// DO, khoảng cách từ M đến mp(ABC) là MH Bài 3: Cho hình chóp S.ABC có tam giác ABC vuông cân ở B, , SA vuông góc với đáy, Tính thể tích của khối chóp S.ABC. Gọi G là trọng tâm tam giác ABC, mặt phẳng qua AG và song song với BC cắt SC, SB lần lượt tại M, N. Tính thể tích của khối chóp S.AMN. Hướng dẫn: Yêu cầu: +Học sinh ghi được thể tích khối SABC và tính. +Biết dùng định lý Talet tìm tỉ lệ các đoạn thẳng để lập tỉ số thể tích hai khối. + Nắm được công thức (*) để lập tỉ số thể tích đối với khối chóp Lời giải: a)Ta có: + + Vậy: b) Gọi I là trung điểm BC. G là trọng tâm,ta có : // BC MN// BC Vậy: Bài tập 4 Cho tam giác ABC vuông cân ở A và . Trên đường thẳng qua C và vuông góc với mặt phẳng (ABC) lấy điểm D sao cho . Mặt phẳng qua C vuông góc với BD, cắt BD tại F và cắt AD tại E. Tính thể tích khối tứ diện ABCD. Chứng minh Tính thể tích khối tứ diện CDEF. Hướng dẫn: Hình vẽ Yêu cầu: +Học sinh chứng minh được đường thẳng vuông góc mặt phẳng. +Nắm được nhu cầu tính các tỉ số ,. +Biết dụng hệ thức trong tam giác vuông để suy ra Lời giải: a)Tính Ta có: b) Ta có: Ta có: c) Tính : Ta có: Mà , chia cho Tương tự: Từ (*) . Vậy Bài 5: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc đáy, . Gọi B’, D’ là hình chiếu của A lần lượt lên SB, SD. Mặt phẳng (AB’D’) cắt SC tại C’. Tính thể tích khối chóp S.ABCD. Chứng minh Tính thể tích khối chóp S.AB’C’D’ Yêu cầu: +Học sinh biết chứng minh + Biết phân thành hai khối chóp bằng nhau: + Sử dụng tỉ số để giải như bài 7. Lời giải: a) Ta có: b) Ta có Ta có Suy ra: c) Tính +Tính : Ta có: vuông cân nên Ta có: Từ +
Tài liệu đính kèm:
 t tich.doc
t tich.doc





