Một số bài toán có liên quan đến góc và khoảng cách
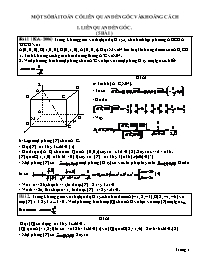
Bài 1 ( KA-2006) Trong không gian với hệ tọa độ Oxyz , cho hình lập phương ABCD.A 'B'C'D' với
A(0; 0; 0), B(1; 0; 0), D(0;1; 0), A'(0; 0;1). Gọi M và N lần lượt là trung điểm của AB, CD
1. Tính khoảng cách giữa hai đường thẳng A'C và MN.
2. Viết phương trình mặt phẳng chứa A'C và tạo với mặt phẳng Oxy một góc α biÕt
Bạn đang xem 20 trang mẫu của tài liệu "Một số bài toán có liên quan đến góc và khoảng cách", để tải tài liệu gốc về máy bạn click vào nút DOWNLOAD ở trên
MỘT SỐ BÀI TOÁN CÓ LIÊN QUAN ĐẾN GÓC VÀ KHOẢNG CÁCH I. LIÊN QUAN ĐẾN GÓC . (5 BÀI ) Bµi 1 ( KA-2006) Trong không gian với hệ tọa độ Oxyz , cho hình lập phương ABCD.A 'B'C'D' với A(0; 0; 0), B(1; 0; 0), D(0;1; 0), A'(0; 0;1). Gọi M và N lần lượt là trung điểm của AB, CD 1. Tính khoảng cách giữa hai đường thẳng A'C và MN. 2. Viết phương trình mặt phẳng chứa A'C và tạo với mặt phẳng Oxy một góc α biÕt Z A B C D’ B’ C’ D’ A’ M N GIẢI a/ Tính h( A’C,MN). - Ta có : - Do đó : - Vậy : b/ Lập mặt phẳng (P) chứa A’C . - Gọi (P) : ax+by+cz+d=0 (1) - Do đi qua (A’C) cho nên : Qua A’(0;0;1) suy ra : c+d=0 (2). Suy ra c=-d = a+b . (P) qua C(1;1;0) : a+b+d =0 (3) suy ra : (P) : ax+by+(a+b)z-(a+b)=0 (*) - Mặt phẳng (P) có : , mặt phẳng (Oxy) có véc tơ pháp tuyến là . Do đó ta có : (4) - Với : a=-2b, chọn b=-1, ta được (P) : 2x-y+z-1=0 - Với b=-2a , thì chọn a=1 , ta được (P) : x-2y-z+1=0 . Bài 2. Trong không gian với hệ tọa độ Oxyz cho hai điểm A(-1; 2; -3), B(2; -1; -6) và mp(P): x + 2y + z -3= 0 . Viết phương trình mp(Q) chứa AB và tạo với mp(P) một góc a thỏa mãn: GIẢI Gọi (Q) có dạng : ax+by+cz+d=0 . (Q) qua A(-1;2;-3) ta có : -a+2b-3c+d=0 (1) và (Q) qua B(2;-1;-6) : 2a-b-6c+d=0 .(2) - Mặt phẳng (P) có . Suy ra (3) - Từ (1) và (2) ta có : . - Thay vào (3) : - Vậy có hai mặt phẳng : (Q): -4x+y-3z-15=0 và (Q’): -x+y-3=0 . Bài 3. Trong không gian tọa độ Oxyz cho hai điểm A(2; -1; 1), B(0; 1: -2) và đường thẳng (d): . Viết phương trình đường thẳng (D) đi qua giao điểm của đường thẳng (d) với mặt phẳng (OAB), nằm trong mặt phẳng (OAB) và hợp với đường thẳng (d) một góc a sao cho . GIẢI - Ta có : - Do đó : mp(OAB): x+4y+2z=0 (1) . Gọi M là giao của d với (OAB) thì tọa độ của M là nghiệm của hệ : - Vì - Do đó : - Suy ra : - Với - Với b=c, thay vào (2) ta có a=-6c Bài 3. Trong không gian tọa độ Oxyz, viết phương trình đường thẳng D đi qua điểm A(0;1;-2), vuông góc với đường thẳng và tạo với mặt phẳng (P): 2x + y - z +5 = 0 một góc 300. GIẢI * Đường thẳng d có véc tơ chỉ phương , đường thẳng D có véc tơ chỉ phương . Mặt phẳng (P) có .Gọi . - Do đó : - Vì : - Thay (3) vào (2) ta được : - Với c-0, thay vào (3) ta có b=a suy ra - Với : c=-2a , thay vòa (3) ta có b=-a Bài 4. Trong không gian với hệ trục toạ độ Đềcác Oxyz, cho hai đường thẳng : D1 : , và D2 : a/Chứng minh hai đường thẳng D1 và D2 chéo nhau. b/Viết phương trình mặt phẳng (P) chứa đường thẳng D2 và tạo với đường thẳng D1 một góc 300 GIẢI a/Chứng minh hai đường thẳng D1 và D2 chéo nhau: * Đường thẳng D1 có véc tơ chỉ phương và qua O(0;0;0), còn qua B(1;-1;1) Có véc tơ chỉ phương (1) Mặt khác : . Kết hợp với (1) suy ra hai đường thẳng D1 và D2 chéo nhau . b/ Viết phương trình (P). Đường thẳng *. Vì (P) chứa thuộc chùm : Mặt khác (P) tạo với đường thẳng D1 một góc thì : - Thay (3) vào (*) ta có : - Với . Với m=-n thì (P): 2nx-ny-nz-2n=0 , Hay (P): 2x-y-z-2 =0 . Bài 5. Trong kh«ng gian víi hÖ täa ®é Oxyz cho hai ®êng th¼ng d vµ d’ lÇn lît cã ph¬ng tr×nh : d : vµ d’ : . ViÕt ph¬ng tr×nh mÆt ph¼ng (P) ®i qua d vµ t¹o víi d’ mét gãc GIẢI Tương tự như bài 4, ta chuyển d sang dạng là giao của hai mặt phẳng : x-z=0 và x+y-2=0 . Do đó (P) thuộc chùm : m(x-z)+n(x+y-2)=0 ; hay : (m+n)x+ny-mz-2n=0 (1) Đường thẳng d’ có . Vì (P) tạo với d’ một góc bằng cho nên - Với m=-2n thay vào (1) thì (P): -nx+ny+2nz-2n=0 ; hay (P):-x+2y+2z-2=0 . - Với n=-2m thay vào (1) thì (P): -mx-2my-mz+4m=0 ; hay (P): -x-2y-z+4=0 . II. LIÊN QUAN ĐẾN KHOẢNG CÁCH ( 32 BÀI ) Bài 1.(ĐH_KD-2009). Trong không gian tọa độ Oxyz , cho tứ diện ABCD có tọa độ các đỉnh A(1;2;1),B(-2;1;3), C(2;-1;1),D(0;3;1).Viết phương trình mặt phẳng (P) đi qua A và B sao cho khoảng cách từ điểm C đến mặt phẳng (P) bằng khoảng cách từ điểm D đến mặt phẳng (P). GIẢI - Mặt phẳng (P) có dạng : ax+by+cz+d=0 . - (P) qua A(1;2;1) thì : a+2b+c+d=0 (1) . (P) qua B(-2;1;3) thì : -2a+b+3c+d=0 (2). - Theo giả thiết : h(C,P)=h(D,P) Nếu a=b thay vào (1) và (2) : Nếu : a+b+c+d=0 thay vào (1) và (2) : Bài 2. Trong không gian tọa độ Oxyz , cho mặt phẳng (P) và đường thẳng d lần lượt có phương trình : (P): 2x-y-2z-2=0 và (d): . Viết phương trình mặt cầu (S) có tâm I thuộc (d), I cách (P) một khoảng bằng 2 và (P) cắt (S) theo một đường tròn giao tuyến có bán kính bằng 3 GIẢI Gọi (S) có tâm I(a;b;c) và bán kính R . Theo giả thiết : - I thuộc d thì I( -t;2t-1;t+2) (1). h(I,P)=2 - (P) cắt (S) theo giao tuyến là đường tròn (C ) tâm H và bán kính r=3 thì : - Thay (1) vào (2) : - Vậy có 2 mặt cầu (S) : Bài 3. Trong không gian tọa độ Oxyz cho đường thẳng (d): và hai điểm A(2; -1; 1), B(0; 1: -2). Tìm tọa độ điểm M thuộc đường thẳng (d) sao cho tam giác ABM có diện tích nhỏ nhất. GIẢI - Nếu M thuộc d thì M có tọ độ M=(t;3-t;2t-1) . - Ta có : - Do đó : - Vậy : min S = khi t=-5 và M=( -5;8;-11). Bài 4. Trong không gian với hệ toạ độ Oxyz, cho hai điểm A(1;5;0), B(3;3;6) và đường thẳng . Tìm toạ độ điểm M thuộc đường thẳng (D) để tam giác MAB có diện tích nhỏ nhất. GIẢI Cách giải tương tự như bài 3 . - Nếu M thuộc d thì M có tọ độ M=(2t-1;1-t;2t) . - Ta có : - Do đó : - Vậy : min S = khi . Bài 5. Trong không gian với hệ trục tọa độ Oxyz, cho hai điểm A(4;9;-9), B(-10;13;1) và mặt phẳng (P): x + 5y - 7z - 5 = 0. Tìm tọa độ điểm M trên mặt phẳng (P) sao cho MA2 + MB2 đạt giá trị nhỏ nhất. GIẢI Gọi M (x;y;z) thuộc (P) thì ta có : x+5y-7z-5=0 (1). Khi đó : Do đó Hay : (2) . Từ (1) -75=1(x+3)+5(y-11)-7(z+4) . Theo bất đẳng thức Bu nhe cốp ski suy ra : Do đó : Và : Dấu đẳng thức xảy ra khi : Ta còn cách khác , sử dụng hệ thức trung tuyến : Gọi I là trung điểm của AB . Ta có : Với : . Và I(-3;11;-4) suy ra Do đó : . Vậy (*) ( Kết quả như trên ). Bài 6. Trong không gian với hệ toạ độ Oxyz, cho ba điểm A(5; 8; -11), B(3; 5; -4), C(2; 1; -6) và đường thẳng thẳng (d): . Xác định toạ độ điểm M thuộc (d) sao cho đạt giá trị nhỏ nhất. GIẢI Điểm M thuộc d thì M(2t+1;2+2t;1+t) , cho nên : Dấu đẳng thức xảy ra khi : Bài 7. Trong không gian hệ toạ độ Oxyz, cho tứ diện ABCD với A(1; -1; 2), B(1; 3; 0), C(-3; 4; 1) và D(1; 2; 1). Viết phương trình mặt phẳng (P) đi qua A, B sao cho khoảng cách từ C đến (P) bằng khoảng cách từ D đến (P). GIẢI Mặt phẳng (P) có dạng : ax+by+cz+d=0 . Nếu (P) qua A(1;-1;2) thì ta có phương trình : a-b+2c+d=0 (1) Nếu (P) qua B(1;3;0) thì ta có phương trình : a+3b+d=0 (2) Theo giả thiết : h(C,P)=h(D,P) cho nên ta có : Kết hợp với hai phương trình (1) và (2) ta có hai hệ xét cho hai trường hợp : Trường hợp 1: Trường hợp 2: Bài 7.Trong không gian với hệ toạ độ Oxyz, cho mặt phẳng (P): và các điểm A(4;1;5), B(3;0;1), C(-1;2; 0). Tìm toạ độ điểm M thuộc (a) để biểu thức sau đạt giá trị nhỏ nhất: . GIẢI Gọi M(x;y;z) thuộc (P) thì ta có phương trình : 3x-3y+2z+37=0 (1). Khi đó ta có : và : Lấy (2)+(3)+(4) vế với vế ta được : Áp dụng bất đẳng thức Bu nhe cốp ski cho phương trình (1) : Suy ra : Hay : . Vậy : Dấu đẳng thức xảy ra khi : Bài 8. Trong không gian với hệ toạ độ , cho và mặt phẳng (P): . Tìm toạ độ điểm M thuộc (P) sao cho tam giác vuông cân tại B. GIẢI Gọi M=(x;y;z) . Nếu M thuộc (P) thì : x-y+z=0 (1). Ta có : . Nếu tam giác MAB vuông cân tại B và kết hợp với (1) thì ta có hệ phương trình : Bài 9. Trong không gian với hệ toạ độ Oxyz, cho đường thẳng (d): và mặt phẳng (P): . Gọi (d’) là hình chiếu của (d) lên mặt phẳng (P). Tìm toạ độ điểm H thuộc (d’) sao cho H cách điểm K(1; 1; 4) một khoảng bằng 5. GIẢI Lập phương trình đường thẳng d’ là hình chiếu vuông góc của d trên (P) . - Tìm tọa độ A là giao của d với (P) . Tọa độ của A là nghiệm của hệ : - Do là hình chiếu vuông góc nên - Vậy d’ qua A(4;-2;3)có véc tơ chỉ phương Tìm tọa độ H . Nếu H thuộc d’ thì H=(t+4;-2-4t;3-3t) (*) ,suy ra Do đó : Vậy : , thay vào (*) ta tìm được tọa độ của H . Bài 10. Trong không gian Oxyz cho hai đường thẳng D1: ; D2: . Đường thẳng D đi qua điểm I(0;3;-1), cắt D1 tại A, cắt D2 tại B. Tính tỷ số =k GIẢI Do A thuộc . B thuộc Ta có : Theo giả thiết : Bài 11. Trong không gian với hệ toạ độ , cho hai đường thẳng D1: ; D1: . Đường vuông góc chung của D1 và D2 cắt D1 tại A, cắt D2 tại B. Tính diện tích D OAB. GIẢI *Do A thuộc . B thuộc Ta có : - Nếu AB là đường vuông góc chung thì : - Gọi S là diện tích tam giác OAB thì : - Do đó : . - Và Bài 12. Trong không gian , cho mặt phẳng (P): 2x + y - 2z + 9 = 0, đường thẳng (d): . Viết phương trình đường thẳng D vuông góc với (P) và thỏa mãn D cắt (d) tại một điểm M cách (P) một khoảng bằng 2. GIẢI Tìm M trên d thì M=(t-1;7t+1;3-t) . Khoảng cách từ M đến (P) là h(M,P)= 2 . Vì D cắt d cho nên D qua M và D (P) . Vì vậy Hoặc : Chú ý : Ta còn có một cách khác như sau Lập mặt phẳng (Q) song song với (P) và cách (P) một khoảng bằng 2 . Do đó (Q) có dạng : 2x+y-2z+m=0 . Ví h(P,Q) = 2 suy ra : Trên (Q) chọn N(-2;-3;1) ta tính h(N,Q)=. Như vậy : có hai mặt phẳng (Q) ; 2x+y-2z+14=0 và 2x+y-2z+2=0 . Bây giờ ta đi tìm tọa độ của M là giao của d với (Q), thì tọa độ M là nghiệm : Hoặc : Bài 13. Trong không gian với hệ tọa độ Oxyz, cho đường thẳng D: và hai điểm A(0;1:-2), B(2;-1;1). Tìm tọa độ điểm C thuộc đường thẳng D sao cho tam giác ABC có diện tích nhỏ nhất. GIẢI Nếu C thuộc D thì có tọa độ là : C=(t+1 ;2-t ;1+2t) Ta có : Gọi S là diện tích tam giác ABC thì : . Dấu đẳng thức xảy ra khi t=-3 , và C=( -2 ;5 ;-5 ) Bài 14. Trong không gian tọa độ Oxyz, cho ba điểm và mặt phẳng . Tìm tọa độ điểm M trên (a) sao cho biểu thức đạt giá trị nhỏ nhất. GIẢI Nếu M thuộc mặt phẳng (1) . Khi đó ta có : Cộng các vế của ba đẳng thức trên ta được : T= Do M thuộc (P) : x+y+2z+2=0 . Áp dụng bất đẳng thức Bu nhe cốp ski cho ba cặp số : (1;1;2) và (x-1;y-1;z-1 ) ta có : . Dấu đẳng thức xảy ra khi xảy ra trường hợp dấu bẳng trong bất đẳng thức Bu nhe cốp ski: Bài 15. Trong không gian tọa độ Oxyz, cho hai điểm A(0;0;-3); B(2;0;-1) và mặt phẳng (P): 3x - y - z +1 = 0. Tìm tọa độ điểm C nằm trên (P) sao cho ABC tam giác đều. GIẢI Nếu M=(x;y;z) thuộc (P) suy ra ; 3x-y-z+1=0 (1). Khi đó ta đi tính : Nếu tam giác ABC là tam giác đều thì ta có hệ phương trình : Vậy điểm M cần tìm là : Bài 16. Trong không gian Oxyz cho mp (P): 3x - 8y + 7z + 4 = 0 và hai điểm A(1; 1; -3), B(3; 1; -1). Tìm tọa độ điểm C thuộc mặt phẳng (P) sao cho tam giác ABC đều. GIẢI Nếu C thuộc (P) thì tọa độ của C=(x;y;z) thỏa mãn : 3x-8y+7z+4=0 (1). Ta có : Nếu tam giác ABC là tam giác đều thì ta có hệ phương trình : Vậy có hai điểm C : Bài 17. Trong không gian tọa độ Oxyz, cho tam giác ABC có A(3; 1; 0), B nằm trên mặt phẳng Oxy và C nằm trên trục Oz. Tìm tọa độ các điểm B, C sao cho H(2; 1; 1) là trực tâm của tam giác ABC. GIẢI Nếu B nằm trên mp(Oxy) thì B( x;y;0), còn C nằm trên trục Oz thì C(0;0;z) . Gọi H là trực tâm của tam giác ABC thì nó là giao của ba đường cao hạ từ ba đỉnh của tam giác có nghĩa là ta có hệ ba phương trình : (1) Ta có : Tương tự : Và : Do đó hệ (1) Vậy điểm C cần tìm có tọa độ là C=( t;7-2t;-t ) . ( Có vô số điểm C) Bài 18. Trong không gian với hệ tọa độ Oxyz, cho đường thẳng (d): và điểm M(4 ; 1 ; 6). Đường thẳng (d) cắt mặt cầu (S) tâm là M tại hai điểm A, B sao cho AB = 6. Viết phương trình của mặt cầu (S). GIẢI Đường thẳng d qua N(-5;7;0) vả có véc tơ chỉ phương . Do đó : A B M H d . -Xét tam giác vuông MAH ( H là chân đường vuông góc của M trên d ) , ta có : . Vậy mặt cầu (S) có tâm M(4;1;6) , bán kính R= Có phương trình là : Bài 19. Trong không gian với hệ trục toạ độ Oxyz cho mặt phẳng (P): 2x – y + z + 1 = 0 và hai đường thẳng . Viết phương trình đường thẳng (D) song song với (P); vuông góc với (d1) và cắt (d2) tại E có hoành độ bằng 3. E P GIẢI Đường thẳng qua điểm M(1;-2;3) có véc tơ chỉ phương , và đường thẳng có véc tơ chỉ phương Gọi D là đường thẳng song song với (P) có thì: - - D - D qua E trên với E(3;y;z) - Từ (1) và (2) ta có hệ : - Vậy D qua E(3;-1;6) có . Bài 20. Trong kh«ng gian víi hÖ täa ®é Oxyz cho ®iÓm A(10; 2; -1) vµ ®êng th¼ng d cã ph¬ng tr×nh. LËp ph¬ng tr×nh mÆt ph¼ng (P) ®i qua A, song song víi d vµ kho¶ng c¸ch tõ d tíi (P) lµ lín nhÊt. GIẢI Gọi (P) là mặt phẳng qua A(10;2;-1) và có véc tơ pháp tuyến . Do đó (P) có phương trình là : a(x-10)+b(y-2)+c(z+1)=0 ; Hay (P): ax+by+cz-10a-2b+c=0 (*) Đường thẳng d qua B(1;0;1) và có véc tơ chỉ phương - Nếu (P) song song với d thì - Khoảng cách từ d đến (P) chính là khoảng cách từ M thuộc d đến (P) , với M=(2t+1;t;3t+1) do vậy ta cho t=0 thì M=(1;0;1) : h(M,P)=. (2) . Áp dụng bất đẳng thức Bu nhe cốp ski cho tử số : - Vậy: h(M;P) đạt GTNN bằng khi trường hợp xảy ra dấu bằng trong bất đẳng thức : Bài 21. Cho 2 điểm A(1 ; 2 ; 3), B(-1 ; 4 ; 2) và hai mp : (P): 2x – 6y + 4z + 3 = 0 (Q): x – y + z + 1 = 0 Tìm tọa độ giao điểm K của đường thẳng AB với mp(P). Tìm tọa độ điểm C nằm trên mp(Q) sao cho tam giác ABC là tam giác đều. GIẢI - Đường thẳng (AB) qua A(1;2;3) và có véc tơ chỉ phương do đó (AB) có phương trình là : . Đường thẳng (AB) cắt mặt phẳng (P) tại K , tọ độ K là nghiệm của hệ : Nếu C nằm trên mặt phẳng (Q) thì C(x;y;z) thỏa mãn : x-y+z+1=0 (1). Tam giác ABC đều khi : Từ (1) và (2) ta có : . (2) hoặc Bài 22. Viết phương trình mặt phẳng đi qua điểm M(9; 1; 1) cắt các tia Ox, Oy, Oz tại A, B, C sao cho thể tích tứ diện OABC có giá trị nhỏ nhất GIẢI Gọi A(a;0;0) tuộc Ox,B(0;b;0) thuộc Oy và C(0;0;c) thuộc Oz ( a,b,c khác 0 ) Khi đó mặt phẳng (P) có dạng : . Nếu (P) qua M(9;1;1) thì ta có : . Do thể tích tứ diện Ta áp dụng bất đẳng thức cô si : Từ (2) abc=9bc+ac+ab Dấu đẳng thức xảy ra khi : . Bài 23. Trong không gian với hệ tọa độ 0xyz cho đường thẳng d và hai điểm A(1;-1;2) ,B(3 ;- 4;-2).Tìm điểm I trên đường thẳng d sao cho IA +IB đạt giá trị nhỏ nhất GIẢI A B I A’ d H Nhận xét : Đường thẳng d có véc tơ chỉ phương . Cho nên đường thẳng d song song với (AB). Do đó (AB) và d cùng thuộc một mặt phẳng . Từ đó , theo kết quả của hình học phẳng , ta làm như sau : - Tìm tọa độ điểm A’ đối xứng với điểm A qua đường thẳng d . - Lập đường thẳng d’ qua A’ và B - Tìm tọa độ I là giao của (A’B) với d . Theo cách làm trên , rõ ràng dường thẳng d là trung trực của AA’ cho nên IA=IA’ , cho nên : IA+IB=IA’+IB=A’B . Nếu có I’ thuộc d thì I’A+I’B>A’B . Vậy I là điểm duy nhất . - Cũng theo nhận xét trên thì IH là đường trung bình của tam giác A’BA cho nên AB=2IH. Hay IA’=IB=IA (*) . Do đó : Nếu I nằm trên d thì điểm I có tọa độ là I=(2+4t;-6t;-8t-1) . Từ đó ta có : Tương tự : Từ (*) : IA=IB = Hay : Tọa độ I thỏa mãn yêu cầu là : Chú ý : Năm 1998 ĐH Thái nguyên K-A+B cũng đã ra dạng bài tập này rồi . * Đề thi : Cho điểm A(1;2;-1) và điểm B(7;-2;3) , đường thẳng d là giao của hai mặt phẳng có phương trình : 2x+3y-4=0 và y+z-4=0 . a/ Chứng tỏ d và đường thẳng (AB) cùng thuộc một mặt phẳng . Viết phương trình mặt phẳng đó . b/ Tìm tọa độ giao điểm của d với mặt phẳng trung trực của đoạn thẳng AB . c/ Tìm điểm I thuộc d sao cho chu vi tam giác ABI có giá trị nhỏ nhất ? Tính chu vi tam giác ABI với điểm I tìm được . Bài 24. Trong không gian với hệ toạ độ Oxyz, cho hai điểm A(1;2; -1), B(7; -2; 3) và đường thẳng d có phương trình . Tìm trên d những điểm M sao cho tổng khoảng cách từ M đến A và B là nhỏ nhất. GIẢI A B M A’ d H Nhận xét : Đường thẳng d có véc tơ chỉ phương . Cho nên đường thẳng d song song với (AB). Do đó (AB) và d cùng thuộc một mặt phẳng . Từ đó , theo kết quả của hình học phẳng , ta làm như sau : - Tìm tọa độ điểm A’ đối xứng với điểm A qua đường thẳng d . - Lập đường thẳng d’ qua A’ và B - Tìm tọa độ M là giao của (A’B) với d . Theo cách làm trên , rõ ràng dường thẳng d là trung trực của AA’ cho nên MA=MA’ , cho nên : MA+MB=MA’+MB=A’B . Nếu có M’ thuộc d thì M’A+M’B>A’B . Vậy M là điểm duy nhất . - Cũng theo nhận xét trên thì MH là đường trung bình của tam giác A’BA cho nên AB=2MH. Hay MA’=MB=MA (*) . Do đó : Nếu M nằm trên d thì điểm I có tọa độ là M=(2+3t;-2t;4+2t) . Từ đó ta có : Tương tự : Từ (*) : MA=MB == Hay : Tọa độ I thỏa mãn yêu cầu là : M=(2;0;4 ). Bài 25. Trong không gian với hệ trục toạ độ Oxyz cho và đường thẳng , điểm A( -2; 3; 4). Gọi D là đường thẳng nằm trên (P) đi qua giao điểm của ( d) và (P) đồng thời vuông góc với d. Tìm trên D điểm M sao cho khoảng cách AM ngắn nhất. GIẢI Gọi B(x;y;z) là giao của d với (P) thì tọa độ của B là nghiệm của hệ : d B A P M - Do D nằm trên (P) suy ra , . - Vậy D qua B(-1;0;4) và có véc tơ chỉ phương . . - Nếu M thuộc thì M=(-1+t;-t;4-t) Do vậy AM đạt GTNN= khi . Bài 26. Trong Không gian với hệ tọa độ Oxyz.Cho đường thẳng và điểm Tìm tọa độ các điểm E và F thuộc đường thẳng để tam giác AEF là tam giác đều. GIẢI - Nếu E,F đều thuộc (1) - Ta lại có : Tương tự : - Nếu tam giác AEF là tam giác đều thì ta có hệ : Thay hai cặp t tìm được vào tọa độ của M , ta tìm được hai cặp E,F trên . Bài 27. Trong không gian với hệ toạ độ Oxyz, cho M(2; 1; 2) và đường thẳng (d): . Tìm trên (d) hai điểm A, B sao cho tam giác MAB đều. GiẢI Nếu A,B thuộc d thì ta có : . Nếu tam giác AMB là tam giác đều thì ta có hệ : Vậy thay hai cặp t tìm được ở trên vào tọa độ của A,B ta có kết quả . Bài 28. Trong không gian với hệ tọa độ Đêcác vuông góc Oxyz cho Cho mặt phẳng và các đường thẳng Tìm điểm M thuộc d 1, N thuộc d 2 sao cho MN song song với (P) và đường thẳng MN cách (P) một khoảng bằng 2. GIẢI - M,N cách mặt phẳng (P) một khoảng bằng 2. Như vậy ta tìm được hai cặp M,N : Bài 29. Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng: và . Tìm tọa độ các điểm M thuộc và N thuộc sao cho đường thẳng MN song song với mặt phẳng độ dài đoạn MN bằng . GIẢI - M thuộc . - Theo giả thiết ta có hệ : Bài 30. Trong không gian toạ độ cho đường thẳng d: và mặt phẳng (P): x + y + z + 2 = 0. Gọi M là giao điểm của d và (P). Viết phương trình đường thẳng nằm trong mặt phẳng (P), vuông góc với d đồng thời thoả mãn khoảng cách từ M tới bằng . GIẢI - Tìm tọa độ điểm M là giao của d với (P) , thì tọa độ M là nghiệm của hệ : P d M H - Đường thẳng . Do đó : . -Gọi H (x;y;z) là hình chiếu vuông góc của M trên thì ta có : H thuộc (P) : x+y+z+2=0 (1). Mặt khác theo giả thiết : . Vậy : H=(29;-4;-27) hoặc H=(21;-2;-21) . Do đó có hai đường thẳng có cùng véc tơ chỉ phương qua hai điểm H tìm được : Bài 31. (KB-08 ). Trong không gian với hệ tọa độ Oxyz, Cho ba điểm A(0;1;2), B(2;-2;1), C(-2;0;1). Viết phương trình mặt phẳng (ABC) và tìm điểm M thuộc mặt phẳng 2x + 2y + z – 3 = 0 sao cho MA = MB = MC. GIẢI - Lập mặt phẳng (ABC) qua A(0;1;2) có véc tơ pháp tuyến . Với : Do đó (ABC) có phương trình là : x+2(y-1)-4(z-2)=0 , Hay (ABC): x+2y-4z+6=0 . - Tìm tọa độ điểm M thuộc (P) : 2x+2y+z-3=0 . Nếu M=(x;y;z) thuộc (P) : 2x+2y+z-3=0 (1) . Ta có : - Theo giả thiết , MA=MB=MC thì ta có hệ : Bài 32. Trong kh«ng gian víi hÖ to¹ ®é Oxyz cho hai ®iÓm A(1;4;2),B(-1;2;4) vµ ®êng th¼ng : .T×m to¹ ®é ®iÓm M trªn sao cho: GIẢI Nếu M thuộc thì M=(1-t;t-2;2t ). Khi đó ta có : Theo giả thiết cho :
Tài liệu đính kèm:
 mot so bat tap hinh giai tich hay.doc
mot so bat tap hinh giai tich hay.doc





