Ma trận đề thi học kỳ 2 – Toán 11 Nâng cao

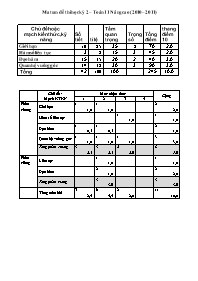
Matran đề thi học kỳ 2 – Toán 11 Nâng cao (2010 – 2011)
Chủ đề hoặc 
mạch kiến thức, kỹ năng
Số tiết
tỉ lệ
Tầm 
quan trọng
Trọng 
số
Tổng 
điểm
thang 
điểm 10
Giới hạn
10
25
35
2
70
2.0
Hàm số liên tục
3
8
15
3
45
2.0
Đạo hàm
15
35
20
2
40
3.0
Quan hệ vuông góc
14
32
30
3
90
3.0
 Tổng
42
100
100
245
10.0
Chủ đề - 
Mạch KTKN
Mức nhận thức
Cộng
1
2
3
4
Phần chung
Giới hạn
1
1,0
1
1,0
2
2,0
Hàm số liên tục
1
1,0
1
1,0
Đạo hàm
1
	0,5
1
	0,5
2
1,0
Quan hệ vuông góc
1
	1,0
1
	1,0
1
	1,0
3
3,0
Tổng phần chung
3
2,5
3
2,5
2
	2,0
8
7,0
Phần riêng
Liên tục
1
1,0
1
1,0
Đạo hàm
2
1,0
2
2,0
Tổng phần riêng
3
3,0
3
3,0
Tổng toàn bài
3
2,5
6
5,5
2
2,0
11
10,0
KHUNG MA TRẬN ĐỀ KIỂM TRA 
TOÁN 11 HỌC KÌ 2
(Dùng cho loại đề kiểm tra TL)
Ma trận 1
Chủ đề - 
Mạch KTKN
Mức nhận thức
Cộng
1
2
3
4
Phần chung
Giới hạn
1
1,0
1
1,0
2
2,0
Hàm số liên tục
1
1,0
1
1,0
Đạo hàm
1
	0,5
1
	0,5
2
1,0
Quan hệ vuông góc
1
	1,0
1
	1,0
1
	1,0
3
3,0
Tổng phần chung
3
2,5
3
2,5
2
	2,0
8
7,0
Phần riêng
Liên tục
1
1,0
1
1,0
Đạo hàm
2
1,0
2
2,0
Tổng phần riêng
3
3,0
3
3,0
Tổng toàn bài
3
2,5
6
5,5
2
2,0
11
10,0
	Diễn giải:
	1) Chủ đề	– Hình học:	3,0 điểm
	– Đại số & Giải tích:	7,0 điểm	+ Giới hạn:	2,0 điểm
	+ Liên tục:	2,0 điểm	
	+ Đạo hàm:	3,0 điểm
	2) Mức nhận biết:
	– Chuẩn hoá:	8,0 điểm	(hoặc 7,0 điểm)
	– Phân hoá:	2,0 điểm	(hoặc 3,0 điểm)
	Mô tả chi tiết:
I. Phần chung:
	Câu 1: Tính giới hạn của hàm số và dãy số (gồm 2 câu nhỏ)
	Câu 2: Tìm điều kiện để hàm số liên tục tại một điểm hoặc xét tính liên tục của hàm số trên 	tập xác định của nó.	
	Câu 3: Tính đạo hàm của hàm số (gồm 2 câu nhỏ)
	Câu 4: Bài toán hình học không gian (gồm 3 câu nhỏ)
II. Phần riêng:
 1) Theo chương trình chuẩn
	Câu 5a: Ứng dụng tính liên tục của hàm số để chứng minh sự tồn tại nghiệm của phương 	trình.
	Câu 6a: Sử dụng đạo hàm để giải phương trình, bất phương trình; viết phương trình tiếp 	tuyến của đồ thị hàm số tại một điểm thuộc đồ thị (gồm 2 câu nhỏ).
 2) Theo chương trình nâng cao
	Câu 5b: Ứng dụng tính liên tục của hàm số để chứng minh sự tồn tại nghiệm của phương 	trình.	
	Câu 6b: Sử dụng đạo hàm để giải phương trình, bất phương trình; viết phương trình tiếp 	tuyến của đồ thị hàm số với hệ số góc cho trước (gồm 2 câu nhỏ).