Kiểm tra học kỳ II môn Toán – Lớp 12 THPT

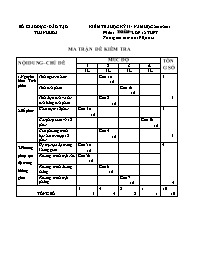
SỞ GIÁO DỤC - ĐÀO TẠO	KIỂM TRA HỌC KỲ II - NĂM HỌC 2010-2011
	THANH HÓA	Moân : TOAÙN – LỚP 12 THPT 
 	Thời gian làm bài: 90 phút 
MA TRẬN ĐỀ KIỂM TRA
NỘI DUNG – CHỦ ĐỀ
MỨC ĐỘ
TỔNG SỐ
1
2
3
4
TL
TL
TL
TL
1.Nguyên hàm Tích phân
Tính nguyên hàm
Câu1a
 1đ
3
 3
Tính tích phân
Câu1b
 1đ
Tính diện tích và thể tích bằng tích phân
Câu2
 1đ
2.Số phức
Khái niệm số phức
Câu3a
 1đ
3
 3
Các phép toán về số phức
Câu3b
 1đ
Giải phương trình bậc hai trên tập số phức
Câu4
 1đ
3.Phương pháp tọa độ trong không gian
Hệ trục tọa độ trong không gian
Câu5a
 1đ
4
 4
Phương trình mặt cầu
Câu5b
 1đ
Phương trình đường thẳng
Câu6
 1đ
Phương trình mặt phẳng
Câu7
 1đ
TỔNG SỐ
3
 3
4
 4
2
 2
1
 1
10
 10
Chú thích: 
	a) Đề được thiết kế với tỉ lệ: 30% nhận biết + 40% thông hiểu + 30% vận dụng và vận dụng khác, tất cả các câu đều tự luận.
	b) Giải tích và hình học có tỉ lệ điểm là : 6:4
	c) Cấu trúc câu hỏi:
	- Số lượng câu hỏi là 10.
	d) Bản mô tả:
Câu 1.a: Tìm nguyên hàm bằng cách dùng trưc tiếp bảng nguyên hàm cơ bản
Câu 1.b: Sử dụng tính chất tích phân của tổng hiệu rồi tính tích phân bằng hàm hợp và tích phân từng phần cơ bản( một lần)
Câu 2: sử dụng tích phân tính diện tích hình phẳng giới hạn bởi một parapol và một đường thẳng.
Câu 3 a: Nhận biết các khái niệm cơ bản về số phức như phần thực, phần ảo.
Câu 3 b: Vận dụng các phép toán của số phức để tính lũy thừa bậc cao của số phức là một căn của số i
Câu 4: Giải phương trình bậc hai với hệ số thực có đenta âm trên tập số phức
Câu 5 a: Nhớ và sử dụng công thức tìm tọa độ một vecto khi biết điểm đầu và điểm cuối, công thức độ dài dài thẳng
Câu 5 b : Tìm tọa độ tâm và bán kính mặt cầu khi biết phương trình mặt cầu
Câu 6: Viết phương trình tham số của một đường thẳng đi qua một điểm và vuông góc với một mp cho trước
Câu 7: Viết phương trình tổng quát của mặt phẳng chứa hai đường thẳng song song
SỞ GIÁO DỤC - ĐÀO TẠO	KIỂM TRA HỌC KỲ II - NĂM HỌC 2010-2011
	THANH HÓA	Moân : TOAÙN – LỚP 12 THPT 
	ĐỀ CHÍNH THỨC	Thời gian làm bài : 90 phút
Câu 1: (2đ)
a.Tính nguyên hàm b.Tính tích phân J= (ecosx-x)sinxdx 
Câu 2: (1đ)
Tính diện tích hình phẳng gới hạn bởi (P) y=x2 - 2x - 3 và đường thẳng y= -3
Câu 3: (2đ)
a. Tìm phần thực và phần ảo của số phức z = 4-3i. b. Tính ( + i )2011 
Câu 4: (1đ) Giải phương trình sau trên tập số phức z2-z+3=0
Câu 5: (2đ)
a. Cho hai điểm A(1;-1,3) và B(0;1;1). Tìm tọa độ vectơ và độ dài đoạn thẳng AB.
b.Tìm tâm I và bán kính R của mặt cầu (S): 
Câu 6: Viết phương trình chính tắc của đường thẳng d đi qua điểm M(0;-3;4) và vuông góc với mặt phẳng (P): 4x-3y+5z-2=0
Câu 7: Viết phương trình mặt phẳng (Q) chứa hai đường thẳng 
d1: và d2: 
Hết.
SỞ GIÁO DỤC - ĐÀO TẠO	KIỂM TRA HỌC KỲ I - NĂM HỌC 2010-2011
	THANH HÓA	Moân : TOAÙN – LỚP 12 THPT 
	ĐỀ CHÍNH THỨC	Thời gian làm bài : 90 phút
ĐÁP ÁN VÀ THANG ĐIỂM
CÂU
ý
NỘI DUNG
ĐIỂM
1
a
 =
0,5
0,5
B
 J= ecosxsinxdx -xsinxdx
Ta có: ecosxsinxdx = - ecosx dcosx=- ecosx = e- 1 
Và xsinxdx = - x.dcosx = -xcosx + cosxdx =-xcosx + sinx= 1.
Suy ra J = e -1 -1 =e - 2
0.25
0,25
0,25
0,25
2
Xét phương trình x2-2x-3= -3 
 (đvdt)
0,25
0,25
0,5
3
a
Phần thực của z là 4
Phần ảo của z là - 3 
0,5
0,5
b
Ta có : ( + i )3= - 1
( + i )2011=( ( + i )3 )670 ( + i )
=(-1)670 ( + I )= + i 
0,25
0,25
0,5
4
z2-z+3=0
Ta có :D=- 11< 0 Þ phương trình đã cho có hai nghiệm phức phân biệt:
z1,2= 
0,5
0,5
5
a
AB=3
0,5
0,5
b
Tâm I(0;1;-3)
R=2
0,5
0.5
6
(P) có vtpt =(4;-3;5)
Vì d (P) nên =(4;-3;5) là vtcp của đường thẳng d
Phương trình tham số của d là 
0,25
0,25
0,5
7
Ta có: d1 đi qua A(1;2;0) và có vtcp =(1;2;-2)
 d2 đi qua B(-1;-1;1) và d1//d2
mp( Q) đi qua A và có vtpt 
Phương trình của mp(Q): 4x-3y+z+2=0
0,25
0.25
0,5
Chú ý: mọi cách khác giải đúng vẫn được điểm tối đa