Kiểm tra học kỳ I môn Toán lớp 12 ban cơ bản
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a, cạnh bên hợp với đáy một góc 600
a/ (1,5đ)Tính diện tích xung quanh của hình chóp S.ABCD
b/ (2,5đ) Mặt phẳng ( ) đi qua A song song với BD và vuông góc với SC cắt SB,SC,SD theo
Bạn đang xem tài liệu "Kiểm tra học kỳ I môn Toán lớp 12 ban cơ bản", để tải tài liệu gốc về máy bạn click vào nút DOWNLOAD ở trên
KIỂM TRA HỌC KỲ I
MÔN TOÁN LỚP 12 BAN CƠ BẢN
Câu 1: (3đ) Cho hàm số:
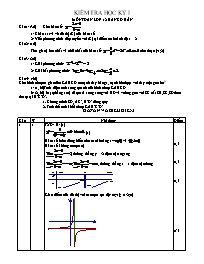
1/ Khảo sát và vẽ đồ thị (C) của hàm số
2/ Viết phương trình tiếp tuyến với (C) tại điểm có hoành độ x = 2
Câu 2: (1đ)
Tìm giá trị lớn nhất và nhỏ nhất của hàm số: trên đoạn [-1;2]
Câu 3: (2đ)
1/ Giải phương trình:
2/ Giải bất phương trình:
Câu 4: (4đ)
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a, cạnh bên hợp với đáy một góc 600
a/ (1,5đ)Tính diện tích xung quanh của hình chóp S.ABCD
b/ (2,5đ) Mặt phẳng () đi qua A song song với BD và vuông góc với SC cắt SB,SC,SD theo thứ tự tại B’C’D’.
1. Chứng minh SO, AC’, B’D’ đồng quy
2. Tính thể tích khối chóp S.AB’C’D’
ĐÁP ÁN VÀ BIỂU ĐIỂM
Câu
Ý
Nội dung
Điểm
1
1
TXĐ: R\{1}
R\{1}
Hàm số luôn đồng biến trên các khoảng ( và
Hàm số không có cực trị
, đường thẳng y = -2 tiệm cận ngang
, đường thẳng x = 1 tiệm cận đứng
Giao điểm của đồ thị với các trục tọa độ: (0;-1); (1/2;0)
0,5
0,5
0,5
0’5
2
Phương trình tiếp tuyến là: y = x - 5
0,25
0,25
0,5
2
y’ = x2 – 4x +3 ,
y’ = 0
y(-1) = , y(2) = , y(1) =
0,25
0,25
0,25
0,25
3
1
Đặt t = , t>0 2t2 -3t -2 = 0
t= 2 = 2 x = 1
0,25
0,5
0,25
2
(1)
Điều kiện x > 0
0,25
0,25
0,25
0,25
4
1
Gọi O là tâm của đáy thì SO(ABCD)
Gọi E là trung điểm BC,
Sxq =
0,5
0,5
0,5
2.1
(//BD (cắt (SBD) theo giao tuyến B’D’// BD
Gọi I là giao điểm của SO và AC’ (1)
(2 )
(1) & (2) SO, AC’, B’D’ đồng quy
0,25
0,5
0,25
2.2
SAC đều AC’SCC’ là trung điểm của SC
I là trọng tâm SAC
AC’=SO=
SC’=
0,25
0,25
0,25
0,25
0,5
Tài liệu đính kèm:
 De thi ky I.doc
De thi ky I.doc





