Kiểm tra 1 tiết chương IV Đại số (cơ bản) lớp 11
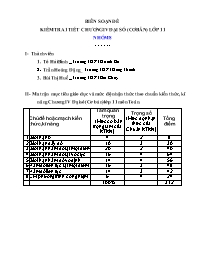
Chủ đề hoặc mạch kiến thức, kĩ năng
Giới hạn 0
Giới hạn dãy số
Giới hạn hàm số tại một điểm
Giới hạn hàm số tại vô cực
Giới hạn hàm số vô định
Hàm số liên tục tại một điểm
Hàm số liên tục
CM phương trình có nghiệm
Bạn đang xem tài liệu "Kiểm tra 1 tiết chương IV Đại số (cơ bản) lớp 11", để tải tài liệu gốc về máy bạn click vào nút DOWNLOAD ở trên
BIÊN SOẠN ĐỀ KIỂM TRA 1 TIẾT CHƯƠNG IV ĐẠI SỐ (CƠ BẢN) LỚP 11 NHÓM 8 ====== Thành viên Tô Hải Bình _ Trường THPT Hoành Bồ Trần Hoàng Đặng _ Trường THPT Đông Thành Bùi Thị Huế _ Trường THPT Bãi Cháy Ma trận mục tiêu giáo dục và mức độ nhận thức theo chuẩn kiến thức, kĩ năng Chương IV Đại só (Cơ bản) lớp 11 môn Toán. Chủ đề hoặc mạch kiến thức, kĩ năng Tầm quan trọng (Mức cơ bản trọng tâm của KTKN) Trọng số (Mức độ nhận thức của Chuẩn KTKN) Tổng điểm 1 Giới hạn 0 4 2 8 2 Giới hạn dãy số 10 3 30 3 Giới hạn hàm số tại một điểm 20 2 40 4 Giới hạn hàm số tại vô cực 16 4 64 5 Giới hạn hàm số vô định 14 4 56 6 Hàm số liên tục tại một điểm 16 3 48 7 Hàm số liên tục 14 3 42 8 CM phương trình có nghiệm 6 4 24 100% 312 MA TRẬN ĐỀ (Chương IV Đại só (Cơ bản) lớp 11 môn Toán) Chủ đề hoặc mạch kiến thức, kĩ năng Mức độ nhận thức - Hình thức câu hỏi Tổng điểm trên 10 1 2 3 4 TNKQ TL TNKQ TL TNKQ TL TNKQ TL Giới hạn 0 Câu 5 1 0.25 0.25 Giới hạn dãy số Câu 1 Câu 6 Câu 16 3 0.25 0.25 0.5 1.00 Giới hạn hàm số tại một điểm Câu 2 Câu 11 Câu 12 3 0.25 0.5 0.5 1.25 Giới hạn hàm số tại vô cực Câu 3 Câu 7 Câu 8 Câu 10 Câu 19 4 0.25 0.25 0.25 0.25 1 2.00 Giới hạn hàm số vô định Câu 4 Câu 13 Câu 9 Câu 20 3 0.25 1 0.25 0.5 2.00 Hàm số liên tục tại một điểm Câu 14 Câu 17 3 0.5 1 1.50 Hàm số liên tục Câu 15 Câu 18 4 0.75 0.5 1.25 CM phương trình có nghiệm Câu 21 1 0.75 0.75 5 7 5 4 21 1.5 3.5 2.5 2.5 10.00 III- GHI CHÚ . - Thiết kế với tỉ lệ: 20% nhận biết + 30% thông hiểu + 50% vận dụng - Kết hợp TNKQ với TL theo tỉ lệ điểm là 2,5 : 7,5 - Cấu trúc câu hỏi: + Số lượng câu hỏi TNKQ là 10 + Số lượng câu hỏi tự luận là 11 + Các câu từ số 1 đến số 4 và câu số 11 là mức nhận biết + Các câu từ số 5 đến số 7 và từ số 12 đến số 15 là mức thông hiểu + Các câu còn lại là mức vận dụng BẢNG MÔ TẢ NỘI DUNG TRONG MỖI Ô Nhận biết Giới hạn dãy số bằng 0 Nhận biết Giới hạn hàm số tại một điểm Nhận biết Giới hạn hàm số tại vô cực Nhận biết Giới hạn hàm số vô định Hiểu được Giới hạn hàm số tại một điểm Hiểu được Giới hạn dãy số Hiểu được Giới hạn hàm số tại vô cực Vận dụng được Giới hạn hàm số tại vô cực Vận dụng được Giới hạn hàm số dạng vô định Vận dụng được Giới hạn hàm số tại vô cực Nhận biết Giới hạn hàm số tại một điểm Hiểu được Giới hạn hàm số tại một điểm Hiểu được Giới hạn hàm số vô định Hiểu được Hàm số liên tục tại một điểm Hiểu được Hàm số liên tục Vận dụng được Giới hạn dãy số Vận dụng được Hàm số liên tục tại một điểm Vận dụng được Hàm số liên tục Vận dụng được Giới hạn hàm số tại vô cực Vận dụng được Giới hạn hàm số vô định Vận dụng được CM phương trình có nghiệm ĐỀ KIỂM TRA 1 tiết Đại số 11 Cơ bản - Môn Toán Thời gian: 90phút (không kể thời gian thu và phát đề). Phần 1: Câu hỏi TNKQ Các câu từ số 1 đến số 10 dưới đây, mỗi câu có 4 phương án lựa chọn là a), b), c) và d) trong đó chỉ có 1 phương án đúng. Hãy khoanh tròn vào chữ cái đứng đầu của phương án mà em cho là đúng. Câu 1: Dãy số nào sau đây có giới hạn khác 0? a. b. c. d. Câu 2: Cho . Khi đó limun bằng a. b. c. d. Câu 3: Cho . Khi đó limun bằng a. 0 b. 1 c. d. Câu 4: bằng a. b. 1 c. 2 d. 3/2 Câu 5: a. -3/2 b. 1 c. 2 d. Câu 6: a. 1/2 b. 1 c. 2 d. Câu 7: a. 1/2 b. 1 c. 2 d. Câu 8: a. 1/2 b. 1/3 c. 2 d. Câu 9: a. -1/4 b. 1 c. 2 d. Câu 10: a. 1/2 b. -5 c. 2 d. Phần 2: Câu hỏi tự luận Câu 11: Tìm: Câu 12: Tìm: Câu 13: Tìm: Câu 14: Tìm: Câu 15: Cho hàm số . Tìm a để hàm số liên tục trên R. Câu 16: Xét tính liên tục của hàm số , tại Câu 17: CMR pt 4x4 +2x2 –x -3 = 0 có ít nhất hai nghiệm phân biệt trong khoảng (-1 , 1). Đáp án Phần 1: Câu hỏi TNKQ Mỗi câu trả lời đúng được 0,25 điểm Câu 1 Câu 2 Câu 3 Câu 4 Câu 5 Câu 6 Câu 7 Câu 8 Câu 9 Câu 10 c d b d a a b b a b Phần 2: Câu hỏi tự luận Câu 11 Tìm: Điểm Giải: . (0,25 điểm) . (0,25 điểm) Câu 12 Tìm: Giải: (0,25 điểm) (0,25 điểm) Câu 13 Tìm: Giải: (0,5 điểm) (0,5 điểm) Câu 14 Tìm: Giải: (0,5 điểm) (0,5 điểm) (0,5 điểm) Câu 15 Cho hàm số , Giải. . (0,5 điểm) Vậy a=2. (0,25 điểm) Câu 16 Xét tính liên tục của hàm số , tại Giải. TXĐ D=R. (0,25 điểm) Ta xét tại điểm x = 4 (0,25 điểm) Vậy f(x) liên tục tại x = 4. (0,25 điểm) Với x¹ 4 thì f(x) là hàm số hữu tỉ xác định với " x¹ 4. (0,25 điểm) Vậy hàm số liên tục trên R. (0,25 điểm) Câu 17 CMR pt 4x4 +2x2 –x -3 = 0 có ít nhất hai nghiệm phân biệt trong khoảng (-1 , 1). Giải. Đặt. f(x) = 4x4 +2x2 –x -3 Tính f(-1) = 4 , f(0) = - 3, f(1) = 2. (0,25 điểm) Nhận xét f(-1) f(0) = -12 < 0, suy ra pt có ít nhất 1 nghiệm phân biệt trong khoảng (-1 , 0). f(0) f(1) = -6 < 0, suy ra pt có ít nhất 1 nghiệm phân biệt trong khoảng (0 , 1). (0,25 điểm) Kết luận. Vậy pt có ít nhất hai nghiệm phân biệt trong khoảng (-1 , 1). (0,25 điểm) ====== Hết ======
Tài liệu đính kèm:
 SP_NHOM 8.doc
SP_NHOM 8.doc





