Hệ thống kiến thức Giải tích 12 - Chương 2: Hàm số lũy thừa, hàm số mũ, hàm số logarit

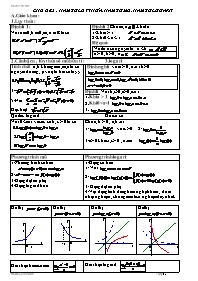
CHỦ ĐỀ 2 : HÀM SỐ LŨY THỪA, HÀM SỐ MŨ, HÀM SỐ LOGARIT
A.Giáo khoa :
1.Lụy thừa :
Định lí 1:
Với a 0; b 0, m, n ta có:
Định lí 2:Cho m, n .khi đó 
1/Khi a > 1: 
2/Khi 0 < a < 1 
Hệ quả: 
Với là n số nguyên lẻ : a < b 
a > 0; b> 0 ; n : 
2.Căn bậc n , lũy thừa số mũ hữu tỉ : 3.logarit
Tính chất :a ,b không âm ,m,n là số nguyên dương , p và q là hai số tùy ý 
3/
5/Nếu :
Đặc biệt : 
Đinh nghĩa: với a > 0; a 1 b> 0
Định lí: Với b,c>0 ;a>0;a1
1.Khi a > 1:
2.Khi 0<a<1 
3. 
Qui tắc logarit : Đổi cơ số :
Với 0 0 ta có:
Cho a, b > 0 , a,b 1
1/ với c >0 2/
3/a> 0 khác1 ,c> 0 , 
Phương trình mũ
Phương trình logarit
1/Phương trình cơ bản: 
2/
3/Dạng đặt ẩn phụ
4/Dạng logarit hóa 
1/Dạng cơ bản :
1/ Với 
2/
3/ Dạng đặt ẩn phụ
4/Vận dụng tính đồng biến nghịch biến , đoán nhận nghiệm , chứng minh có nghiệm duy nhất.
Đồ thị :
Đồ thị 
y
x
o
Đồ thị : 
x
o
y
Đồ thị 
x
o
y
1
a
1
x
o
y
1
-1
a
Giới hạn hàm số mũ 
Giới hạn logarit 
Đạo hàm :hàm số mũ
Đạo hàm hàm số logarit
 ;
 ; 
(lnx)’= ; [ln(U]’= ;
PHẦN BÀI TẬP
A.Bài tập : LŨY THỪA 
Bài tập
Hướng dẫn
Hãy tính: 
a/
b/
c/ d/
e /
a/ =3 b/= 7 c/
d/
e/
B.Tính đạo hàm :
Bài tập
Hướng dẫn
 Bài 1:
 Bài2:
Tính đạo hàm cấp n
a/ f(x) = Tính 
b/f(x) = Tính 
c/f(x) = Tính 
Bài 1: 
Bài 2:
a/ Dùng qui nạp =
b/ = 
c/= 
C.Phương trình mũ -logarit
Bài tập
Hướng dẫn
Bài 1
a/ b/
c/ d/
Bài 2:
a/ b/
c/ d/
e/ f/
Bài 3:
a/ b/) 2.4+ c/
Bài 4:
a/ b/ c/
d/
Bài 5:
a/ Giaûi vaø bieän luaän phöông trình :
b/Ñònh m ñeå ptrình coù nghieäm:
Bài 6:
a/ b/5
c/
Bài 1: Vận dụng 
Bài 2: Đặt ẩn phụ
Bài 3: Qui về cùng cơ số, đặt ẩn phụ
Bài 4:a,b
+Đoán nhận nghiệm c/m nghiệm duy nhất.
+4c,d: Giải tìm x, dùng tính chất đ/biền, n/biến
Bài 6:
Đặt ẩn phụ
D.Phương trình logarit
Bài tập
Hướng dẫn
Bài 1:
a)
b)
Bài 2:
a) b)
Bài 3:
a) b) 
c)
Bài 4:
a)log b)
c)3log d)
Bài 5:
 b)
c) d)
Bài 6:
a) b)
c)5. d) 
Bài 7:
a/log b)1-
c) 
Bài 8: Giải hệ 
Bài 9:
a) b) 
c) d)
Bài 1:
a/Dùng định nghĩa
b/Đ/kiện –Dùng đnghĩa
Bài 2:
a/b/ đổi cơ số , dùng tính chất
Bài 3:
a/b/ Điều kiện – đổi cơ số -đặt ẩn phụ
Bài 4:
a/Dùng định nghĩa
b/ logarit- hóa
Bài 5:
a/ đk – dùng tính chất
b/Dùng đn logarit 
c/Đưa cùng cơ số, đặt ẩn phụ
Bài 6: a/Đặt ẩn phụ
b/ ĐK- đổi cơ số - đặt ẩn phụ
Bài 7:
a/ Tính chất logarit – đưa về p-trình 
Bài 9: 
a/b/Đưa cùng cơ số - đặt ẩn phụ
c/ Đặt ẩn phụ t = 
E. Bất phương trình mũ- logarit :
 I Döïa ñoà thò ta coù ñònh lí :
 Khi a>1 haøm soá ñoàng bieân treân R , nghóa laø: Vôùi moïi 
 Khi 0<a<1 haøm soá nghòch bieán treân R nghóa laø vôùi moïi 
Bài tập
Hướng dẫn
Bài 1:
a/ b/ c/
d/ e/
Bài 2:
a/ b/ c/
Bài 3
a/ b/
c/ d/
Bài 4:
a/ b/
c/ d/
Bài 5:
a/
b/
c/
Bài 6:
a/ b/
c/ d/
Bài 7:
a/ b/
c/ d/
Bài 8:
a/ b/
Bài 9:
a/ b/
c/
d/
Bài 10:
a/
b/
c/ d/
Bài 1:
a/b/c/ đưa cùng cơ số
d/ đưa về cơ số 6 
e/ đặt ẩn phụ
Bài 2:
a/, c/ đặt ẩn phụ
Bài 3:
a/Dùng tính nghịch biến , kết hợp điều kiện
b/ c/ d/ như trên
Bài 4:
a/Đưa cùng cơ số - đặt ẩn phụ 
b/ĐK cơ số,đưa về cơ số 3
c/Vận dụng tính đồng biến
Bài 5:
a/Vận dụng tính nghịch biến –đưa về bất p-trình mũ
b/ĐK cơ số - đưa cơ số 4
c/Ẩn phụ 
Bài 6:
a/ ĐK- và tính đồng biến
b/ Đặt ẩn phụ
c/ Tính nghịch biến – giải bất p-trình có chứa GTT Đ
d/ Đ-K và đưa về cơ số 5
Bài 7:
a/Đk cơ số- ẩn phụ
c/ Tính đồng biến
d/ Đ/k, dùng đồng biến
Bài 8:
a/Đk – đưa về cơ số 8 – dùng tính chất
b/Dùng tính đbiến, nbiến
Bài 9
a/Dùng công thức đổi cơ số
b/Tính đồng biến –Giải B-pt (có chứa GTT Đ)
-----—²–-----