Hệ thống bài tóan thi tốt nghiệp
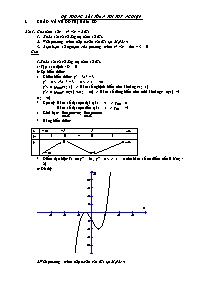
Bài 1: Cho hàm số y = x3 -3x – 2 (C)
1. Khảo sát và vẽ đồg thị hàm số (C).
2. Viết phương trình tiếp tuyến với (C) tại M0(-2;-4)
3. Biện luận số nghiệm của phương trình x3 -3x + 6m – 3 = 0
Giải
1.Khảo sát và vẽ đồg thị hàm số (C).
a/ Tập xác định : D = R
b/ Sự biến thiên:
Bạn đang xem tài liệu "Hệ thống bài tóan thi tốt nghiệp", để tải tài liệu gốc về máy bạn click vào nút DOWNLOAD ở trên
HỆ THỐNG BÀI TÓAN THI TỐT NGHIỆP KHẢO VÀ VẼ ĐỒ THỊ HÀM SỐ Bài 1: Cho hàm số y = x3 -3x – 2 (C) Khảo sát và vẽ đồg thị hàm số (C). Viết phương trình tiếp tuyến với (C) tại M0(-2;-4) Biện luận số nghiệm của phương trình x3 -3x + 6m – 3 = 0 Giải 1.Khảo sát và vẽ đồg thị hàm số (C). a/ Tập xác định : D = R b/ Sự biến thiên: Chiều biến thiên: y’ = 3x2 – 3 y’ = 0 3x2 – 3 = 0 x = 1 y’ Hàm số nghịch biến trên khoảng (-1; 1) y’> 0 (-;-1)(1; +) => Hàm số đồng biến trên mỗi khoảng(-;-1) và (1; +) Cực trị: Hàm số đạt cực đại tại x = -1 => yCĐ = 0 Hàm số đạt cực tiểu tại x = 1 => yCT = -4 Giới hạn: ; Bảng biến thiên: x -1 1 y/ + 0 - 0 + y 0 -4 Điểm đặc biệt: Ta có y” = 6x, y” = 0 x = 0 nên hàm số có điểm uốn là U(0; -2) c/ Đồ thị: 2.Viết phương trình tiếp tuyến với (C) tại M0(-2;-4) Ta có y’(-2) = 9. Vậy phương trình tiếp tuyến với (C) tại điểm M0(-2;-4) là: y = 9x +14 3.Biện luận số nghiệm của phương trình x3 -3x + 6m – 3 = 0 (1) Phương trình (1) x3 -3x – 2 = 1 - 6m . Đây là phương trình hoành độ giao điểm của (C) và đường thẳng d: y = 1 – 6m; Do đó dựa vào đồ thị ta thấy: Nếu thì phuơng trình (1) có 1 nghiệm. Nếu thì phương trình (1) có 2 nghiệm. Nếu -4< m < 0 thì phương trình (1) có 3 nghiệm . Bài 2: Cho hàm số y = 2x3 +3x2 –1 (C) Khảo sát và vẽ đồ thị hàm số (C). Biện luận số nghiệm của phương trình 2x3 +3x2 –1 =m Viết phương trình tiếp tuyến với (C) tại điểm có hoành độ x = -1 Giải 1.Khảo sát và vẽ đồg thị hàm số (C). a/ Tập xác định : D = R b/ Sự biến thiên: Chiều biến thiên: y’ = 6x2 +6x y’ = 0 6x2 +6x = 0 y’ Hàm số nghịch biến trên khoảng (-1; 1) y’> 0 (-;-1)(0; +) => Hàm số đồng biến trên mỗi khoảng(-;-1) và (0; +) Cực trị: Hàm số đạt cực đại tại x = -1 => yCĐ = 0 Hàm số đạt cực tiểu tại x = 0 => yCT = -1 Giới hạn: ; Bảng biến thiên: x -1 0 y/ + 0 - 0 + y 0 -1 Điểm đặc biệt: Ta có y” = 12x + 6, y” = 0 x = nên hàm số có điểm uốn là U(; ) c/ Đồ thị: 2.Biện luận số nghiệm của phương trình 2x3 +3x2 –1 =m (1) Phương trình (1) là phương trình hoành độ giao điểm của (C) và đường thẳng d: y = m; Do đó dựa vào đồ thị ta thấy: Nếu thì phuơng trình (1) có 1 nghiệm. Nếu thì phương trình (1) có 2 nghiệm. Nếu -1< m < 0 thì phương trình (1) có 3 nghiệm . 3.Viết phương trình tiếp tuyến với (C) tại điểm có hoành độ x0 = -1 Với x 0 = -1 ta có: Vậy phương trình tiếp tuyến với (C) tại điểm có hoành độ x0 = -1 là: y = 0 Bài 3: Cho hàm số y = x3 -6x2 +9x - 1 (C) Khảo sát và vẽ đồg thị hàm số (C). Viết phương trình tiếp tuyến với (C) tại giao điểm của đồ thị với trục tung. Tìm m để phương trình x3 -6x2 +9x - 1 = m có 3 nghiệm phân biệt. Giải 1.Khảo sát và vẽ đồ thị hàm số (C). a/ Tập xác định : D = R b/ Sự biến thiên: Chiều biến thiên: y’ = 3x2 – 12x + 9 y’ = 0 3x2 – 12x + 9 = 0 y’ Hàm số nghịch biến trên khoảng (1; 3) y’> 0 (-;1)(3; +) => Hàm số đồng biến trên mỗi khoảng(-;1) và (3;+) Cực trị: Hàm số đạt cực đại tại x = 1 => yCĐ = 3 Hàm số đạt cực tiểu tại x = 3 => yCT = -1 Giới hạn: ; Bảng biến thiên: x 1 3 y/ + 0 - 0 + y 3 -1 Điểm đặc biệt: Ta có y” = 6x -12, y” = 0 x = 2 nên hàm số có điểm uốn là U(2; 1) c/ Đồ thị: 2.Viết phương trình tiếp tuyến với (C) tại giao điểm của đồ thị với trục tung. Giao điểm của (C) với trục tung là: M(0; -1); Ta có y’(0) = 9 Vậy phương trình tiếp tuyến với (C) tại giao điểm của đồ thị với trục tung là: y = 9x – 1 3.Tìm m để phương trình x3 -6x2 +9x - 1 = m (1)có 3 nghiệm phân biệt. Phương trình (1) là phương trình hoành độ giao điểm của (C) và đường thẳng d: y = m; Do đó dựa vào đồ thị ta thấy: Phuuơng trình (1) có 3 nghiệm phân biệt khi đường thẳng d cắt đồ thị (C) tại 3 điểm phân biệt. Khi đó: -1 < m < 3 GIÁ TRỊ LỚN NHẤT, GIÁ TRỊ NHỎ NHẤT CỦA HÀM SỐ Bài 1: Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số: f(x) = x3 + 3x2 -9x+1 trên đoạn [-4;4] Giải f’(x) = 3x2 +6x – 9 Trên khoảng (-4; 4): f’(x) = 0 Ta có: f(-4) = 21; f(1) = -4; f(-3) = 28; f(4) = 77 Vậy và Bài 2: Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số: f(x) = x4 -8x2+16 trên đoạn [-1;3] Giải f’(x) = 4x3 -16x =4x(x2 -4) Trên khoảng (-1; 3): f’(x) = 0 Ta có: f(-1) = 9; f(2) = 0; f(3) = 25 Vậy và Bài 3: Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số: f(x) = 2x3 -3x2-12x +1 trên đoạn [-2;] Giải f’(x) = 6x2 -6x -12 Trên khoảng (-2;): f’(x) = 0 Ta có: f(-2) = 7 ; f(-1) = 8; f(2) = -19; f() = Vậy và f() = PHƯƠNG TRÌNH MŨ Bài 1 : Giải phương trình sau : 2.16x – 17.4x + 8 = 0 (1) Giải Đặt t = 4x (t>0), khi đó : (1) 2t2 -17t +8 = 0 t= 4 4x = 4 x = 1 t = 4x = x = - Vậy phương trình có hai nghiệm : x = 1 và x = - Bài 2 : Giải phương trình sau : 34x+8 – 4.32x+5 + 27 = 0 (1) Giải 34x+8 – 4.32x+5 + 27 = 0 . (32x+5 )2 -4.32x+5 + 27 = 0(2) Đặt t = 32x+5 (t>0) : (2) t2 -4.t + 27 = 0 *Với t = 9, ta có : 32x+5 = 9 2x +5 = 2 x = - *Với t = 27, ta có : 32x+5 = 27 2x +5 = 3 x = -1 Vậy phương trình (1) có hai nghiệm : x = - và x = -1 Bài 3 : Giải phương trình sau : 4x+1 – 6.2x+1 +8 = 0 (1) Giải (1) 4.4x -12.2x + 8 = 0 (2) Đặt t = 2x (t > 0) : (2) 4t2 -12t + 8 = 0 *Với t = 1, ta có : 2x= 1 x = 0 *Với t = 2, ta có : 2x= 2 x = 1 Vậy phương trình (1) có hai nghiệm : x = 0và x = 1 IV. TÍCH PHÂN Bài 1 : Tính tích phân sau : Giải Ta có : sin2x.sin4x = (cos2x – cos6x) = = (sin2x - sin6x= 0 Bài 2 : Tính tích phân sau : Giải I== = -Đặt t = sinx =>dt = cosx.dx -Đổi cận : x = 0 => t = 0 x = => t = 1 Khi đó I = = Bài 3 : Tính tích phân sau : Giải = =I1 + I2 *Tính I1 = : Đặt :u = x =>du = dx dv = sinx.dx => v =-cosx.dx => I1 = = + = = 1 *Tính I2 = : -Đặt t =cosx => dt = -sinx.dx -Đổi cận : : x = 0 => t = 1 x = => t = 0 => I2 = == Vậy I = I1 + I2 = 1 + = V. SỐ PHỨC Bài 1 : Giải phương trình sau trên tập số phức : z2 -3x + 3 = 0 Giải = -3< 0 Vậy phương trình có hai nghiệm phức là : Bài 2 : Giải phương trình sau trên tập số phức : z2 +2z + 2 = 0 Giải ’ = -1< 0 Vậy phương trình có hai nghiệm phức là : Bài 3 : Giải phương trình sau trên tập số phức : z2 +4z +10 = 0 Giải ’ = -6< 0 Vậy phương trình có hai nghiệm phức là : VI. HÌNH HỌC KHÔNG GIAN TỔNG HỢP S A B D C Bài 1 : Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với mp(ABCD), cạnh SC tạo với mặt đáy 1 góc 300. Tính thể tích khối chóp. Giải 300 Ta có Ac = a ; AC là hình chiếu vuông góc của SC lên mp(ABCD), nên góc giữa AC và SC chính bằng góc giữa SC và mặt đáy=> Xét tam giác SAC vuông tại A ta có : SA = AC. tan =a.tan300= Mặt khác SABCD = a2 Vậy thể tích khối chóp là : V = SABCD. SA = .a2.= S A B D C Bài 2 : Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với mp(ABCD), cạnh SB = a. Tính thể tích khối chóp S.ABCD và chứng mình trung điểm I của SC là tâm mặt cầu ngoại tiếp hình chóp S.ABCD. Giải I Xét tam giác SAB vuông tại A có : SA2 = SB2 – AB2 = 3a2 –a2 = 2a2 => SA =a Mặt khác SABCD = a2 Vậy thể tích khối chóp là : V = SABCD. SA = .a2.a= Ta có các góc: ,, và đều nhìn SC dưới 1 góc vuông, nên : IA = IS=IC = IB = ID. Vậy I là tâm mặt cầu ngoại tiếp hình chóp S.ABCD V.PHƯƠNG PHÁP TỌA ĐỘ TRONG KHÔNG GIAN Bài 1 : Trong không gian Oxyz cho A(-2; 0; 1), B(0;10; 3), C(2; 0; -1), D(5;3;-1) Viết phương trình mặt phẳng (ABC). Viết phương trình đường thẳng qua D và vuông góc với mặt phẳng (ABC) Viết phương trình mặt cầu tâm D và tiếp xúc với mặt phẳng (ABC) Giải : 1.Viết phương trình mặt phẳng (ABC). Mặt phẳng (ABC) có cặp vectơ chỉ phương là: và nên mp(ABC) nhận : =[ ,] = (-20; 12; -40) làm 1 vectơ pháp tuyến . Vậy phương trình mp(ABC) đi qua A và có vectơ pháp tuyến là: 5x - 3y + 10 z +36 = 0 2.Viết phương trình đường thẳng qua D và vuông góc với mặt phẳng (ABC) Gọi d là đường thẳng vuông góc với mp(ABC), khi đó d có 1 vectơ chỉ phương là : =(5;-3;10). Mặt khác d đi qua điểm D, nên phương trình tham số của d là: 3.Viết phương trình mặt cầu tâm D và tiếp xúc với mặt phẳng (ABC) Gọi (S) là mặt cầu tâm D và tiếp xúc với mp(ABC) khi đó bán kính của (S) là R = d(D, (ABC)) = Vậy phương trình mặt cầu (S) cần tìm là: (x- 5)2 + (y- 3)2 + (z+1)2 = Bài 2: Cho mặt cầu (S) x2+y2 +z2-6x+4y-2z-86 = 0 và mặt phẳng (): 2x-2y+z+9 = 0 Định tâm và bán kính mặt cầu Viết phương trình đường thẳng (d) qua tâm mặt cầu và vuông góc với () Chứng tỏ () cắt mặt cầu (S) Giải : 1.Định tâm và bán kính mặt cầu x2+y2 +z2-6x+4y-2z-86 = 0 (x-3)2 + (y +4)2 +(z-1)2 = 100 Vậy mặt cầu (S) có tâm là I(3; -4; 1) và có bán kính R = 10 2.Viết phương trình đường thẳng (d) qua tâm mặt cầu và vuông góc với () Do (d) vuông góc với mặt phẳng () nên (d) có 1 vectơ chỉ phương là: = (2; -2; 1) Mặt khác (d) đi qua tâm I(3; -4; 1) của mặt cầu (S) nên phương trình tham số của đường thẳng d là: 3.Chứng tỏ () cắt mặt cầu (S) d(I, ()) =< R Vậy () cắt mặt cầu (S) Bài 3: Cho A(-1;3;2) ; B(4;0;-3) ; C(5;-1;4) ; D(0;6;1) Viết phương trình tham số của BC. Hạ AHBC. Tìm tọa độ điểm H Viết phương trình tổng quát của (BCD). Tính khoảng cách từ A đến mặt phẳng (BCD) Viết phương trình mặt phẳng (P) đi qua điểm (3;-2;1) và vuông góc với đường thẳng (d): Giải : 1.Viết phương trình tham số của BC. Hạ AHBC. Tìm tọa độ điểm H Ta có: =(1; -1; 7) , vậy phương trình tham số của đường thẳng BC là: 2.Viết phương trình tổng quát của (BCD). Tính khoảng cách từ A đến mặt phẳng (BCD) =(1; -1; 7) , =(-4; 6; 4) Mặt phẳng (BCD) có cặp vectơ chỉ phương là: và nên mp(BCD) nhận : =[ ,] = (-46; -32; 2) làm 1 vectơ pháp tuyến => = (23; 16; -1) cũng là 1 vectơ pháp tuyến của mặt phẳng (BCD) Vậy phương trình mp(BCD) đi qua B và có vectơ pháp tuyến là: 23(x -4) + 16(y- 0) - (z +3 ) = 0 23x +16y –z -95= 0 Khoảng cách từ A đến mặt phẳng (BCD): d(A, (BCD)) = 3.Viết phương trình mặt phẳng (P) đi qua điểm (3;-2;1) và vuông góc với đường thẳng (d): Do mặt phẳng (P) vuông góc với đường thẳng (d) nên (P) có 1 vectơ pháp tuyến là: = (-4; 2; -7) Mặt khác (P) đi qua điểm (3; -2; 1) nên phương trình mặt phẳng (P) là: -4(x - 3) +2(y+2) – 7(z- 1) = 0 4x -2y +7z +23 = 0
Tài liệu đính kèm:
 He thong cac bai toan thi tot nghiep.doc
He thong cac bai toan thi tot nghiep.doc





