Hệ phương trình trong các đề thi đại học
Tài liệu Ôn thi ĐH - CĐ
Hệ phương trình trong các đề thi đại học
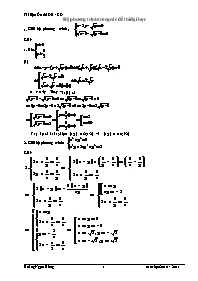
1. Giải hệ phương trình:
Bạn đang xem tài liệu "Hệ phương trình trong các đề thi đại học", để tải tài liệu gốc về máy bạn click vào nút DOWNLOAD ở trên
Hệ phương trình trong các đề thi đại học 1. Giải hệ phương trình: Giải: 1. §k: (1) Û x = 4y Thay vµo (2) cã V©y hÖ cã hai nghiÖm (x;y) = (2;1/2) vµ (x;y) = (10;5/2) 2. Giải hệ phương trình: Giải: 3. Giải hệ phương trình: (x, yÎ R) Giải: ĐK: x + y ³ 0 , x - y ³ 0, y ³ 0 PT(1) Û Từ PT(4) Û y = 0 v 5y = 4x Với y = 0 thế vào PT(2) ta có x = 9 (Không thỏa mãn đk (3)) Với 5y = 4x thế vào PT(2) ta có KL: HPT có 1 nghiệm 4.Giải hệ phương trình: , . Giải: , ta có: Đặt ta có hệ: +) Với ta có hệ:. +) Với ta có hệ: , hệ này vô nghiệm. KL: Vậy hệ đã cho có hai nghiệm: 5. Giải hệ phương trình : Giải: *Biến đổi hệ tương đương với *Đặt ẩn phụ , ta được hệ *Giải hệ trên được nghiệm (u;v) là (1;0) và (-2;-3) *Từ đó giải được nghiệm (x;y) là (1;0) và (-1;0) 6. Giải hệ phương trình: (x, yÎ R) Giải: ĐK: x + y ³ 0 , x - y ³ 0, y ³ 0 PT(1) Û Từ PT(4) Û y = 0 v 5y = 4x Với y = 0 thế vào PT(2) ta có x = 9 (Không thỏa mãn đk (3)) Với 5y = 4x thế vào PT(2) ta có KL: HPT có 1 nghiệm 7. Giải hệ phương trình Giải: ĐK : hệ đưa hệ về dạng Từ đó ta có nghiệm của hệ (-1 ;-1),(1 ;1), (), () 8.Gi¶i hÖ ph¬ng tr×nh: Giải: §iÒu kiÖn: x-1, y1 Céng vÕ theo vÕ råi trõ vÕ theo vÕ ta cã hÖ §Æt u=, v =. Ta cã hÖ lµ nghiÖm cña hÖ 9. Giải hệ phương trình: . Giải: Điều kiện: x+y>0, x-y>0 Đặt: ta có hệ: . Thế (1) vào (2) ta có: . Kết hợp (1) ta có: (vỡ u>v). Từ đó ta có: x =2; y =2.(T/m) KL: Vậy nghiệm của hệ là: (x; y)=(2; 2). 10. Giải hệ phương trình : Giải: +) ĐK: x + 2y = 6 > 0 và x + y + 2 > 0 +) Lấy loga cơ số 2009 và đưa về pt: +) Xét và CM HS đồng biến, từ đó suy ra x2 = y2 Û x= y, x = - y +) Với x = y thế vào (2) và đưa về pt: 3log3(x +2) = 2log2(x + 1) = 6t Đưa pt về dạng , cm pt này có nghiệm duy nhất t = 1 Þ x = y =7 +) Với x = - y thế vào (2) được pt: log3(y + 6) = 1 Þ y = - 3 Þ x = 3 11. Tìm m để hệ phương trình: có nghiệm thực Giải: 2/. Điều kiện: Đặt t = x + 1 Þ tÎ[0; 2]; ta có (1) Û t3 - 3t2 = y3 - 3y2. Hàm số f(u) = u3 - 3u2 nghịch biến trên đoạn [0; 2] nên: (1) Û y = y Û y = x + 1 Þ (2) Û Đặt Þ vÎ[0; 1] Þ (2) Û v2 + 2v - 1 = m. Hàm số g(v) = v2 + 2v - 1 đạt Vậy hệ phương trình có nghiệm khi và chỉ khi -1 £ m£ 2 12. Cho hệ phương trình : Tìm tất cả các giá trị của m để hệ phương trình trên có 3 nghiệm phân biệt (x1; y1), (x2; y2) và (x3; y3) sao cho x1, x2, x3 lập thành một cấp số cộng. Giải: (I) (2) Û y = x - 2 thay vào (1) ta có : (2x - 2)[x2 - 2x + 4 - m] = 0 Û Nhận xét : Nếu pt (*) có 2 nghiệm x1, x2 phân biệt thì : x1 < 1 < x2 và x1 + x2 = 2 YCBT Û pt (*) có 2 nghiệm phân biệt Û D' = 1 - 4 + m > 0 Û m > 3. 13.Cho hệ phương trình : Tìm m để hệ có 3 nghiệm phân biệt (x1;y1);(x2;y2);(x3;y3) sao cho x1;x2;x3 lập thành cấp số cộng .Đồng thời có hai số xi thỏa mãn > 1 Giải: 2.Cho hệ phương trình : ------------------------------------------------------------------------------------------ Tìm m để hệ có 3 nghiệm phân biệt (x1;y1);(x2;y2);(x3;y3) sao cho x1;x2;x3 lập thành cấp số cộng .Đồng thời có hai số xi thỏa mãn > 1 Trước hết phải có 2 nghiệm pbiệt x1 ; x2 Có thể xảy ra ba trường hợp sau đây theo thứ tự lập thành cấp số cộng. +Trường hợp 1 : ; x1 ; x2 +Trường hợp 2 : x1 ; x2 ; +Trường hợp 3 : x1 ; ; x2 Xét thấy Trường hợp 1 ;2 không thỏa mãn. Trường hợp 3 ta có đúng với mọi m > Đồng thời có hai số xi thỏa mãn > 1 ta cần có thêm điều kiện sau Đáp số : m > 3 14. Tìm để hệ phương trình sau có nghiệm : Giải: b)(1 điểm) đ/k .Bất pt ; Vậy và là nghiệm của p/t: T.Rõ ràng hệ trên có nghiệm khi p/t* có 2 nghiệm không âm Bài tập 1.Giải hệ phương trình: 2.Gi¶i hệ ph¬ng tr×nh : 3. Giải hệ phương trình : 4. Gi¶i hệ ph¬ng tr×nh : 5. Giải hệ phương trình : 6. Giải hệ phương trình : 7. Giải hệ phương trình : 8. Giải hệ phương trình : 9. Giải hệ phương trình : 10. Giải hệ phương trình 11. Gi¶i hệ ph¬ng tr×nh 12. Giải hệ phương trình: 13. Giải hệ phương trình 14. Giải hệ
Tài liệu đính kèm:
 He PT hay trong cac de thi DH moi nhat.doc
He PT hay trong cac de thi DH moi nhat.doc





