Giáo án Tự chọn Toán 12 tiết 3-5: Ôn tâp diện tích và tính chất một số hình phẳng quan hệ song song và vuông góc trong không gian

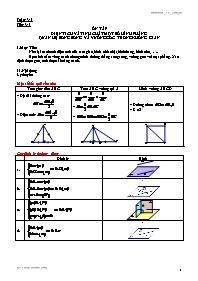
Tuần: 3-5
Tiết: 3-5
ÔN TÂP
DIỆN TÍCH VÀ TÍNH CHẤT MỘT SỐ HÌNH PHẲNG
QUAN HỆ SONG SONG VÀ VUÔNG GÓC TRONG KHÔNG GIAN
I. Mục Tiêu
	Nhớ lại cách tính diện tích của tam giác, hình chữ nhật,hình thang, hình tròn, .
Học sinh nắm vững cách chứng minh đường thẳng song song, vuông góc với mặt phẳng. Xác định được góc, tính được khoảng cách.
II. Nội dung
Lý thuyết:
Một số kết quả cần nhớ
Tam giác đều ABC
Tam ABC vuông tại A
Hình vuông ABCD
* Độ dài đường cao:
* Diện tích: 
* 
* 
* Đường chéo 
* S=AB2
Các định lý thường dùng
Định lý
Hình
a.
b.
c.
d.
Bài tập:
NỘI DUNG
HƯỚNG DẪN-ĐÁP SỐ
Bài 1. Cho hình chóp S.ABCD đáy là hình vuông cạnh a, SA ^ (ABCD), SA =.
a. Chứng minh mp (SAC) ^ mp (SBD).
b. Chứng minh CD ^ (SAD) và tính góc giữa đường thẳng CS và mặt phẳng (SAD).
Bài 2. Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, tam giác SAB là tam giác đều.
Xác định giao tuyến của mặt phẳng (SAB) và (SCD).
M là một điểm trên cạnh BC với BM=x (0<x<a). Mặt phẳng (a) đi qua M song song với SA và CD lần lượt cắt SC, SD, AD tại N, P, Q.
Chứng minh MN//SB.
Chứng minh MNPQ là hình thang cân.
Tính diện tích MNPQ theo a và x.
Bài 3. Cho hình chóp S.ABCD đáy là hình vuông cạnh a, SA=a và vuông góc với mặt phẳng (ABCD).
	a. Chứng minh (SDC)^(SAD).
	b. Tính gần đúng (độ, phút, giây) số đo góc giữa đường thẳng SC và mặt phẳng (ABCD).
	c. Tính khoảng cách giữa hai đường thẳng chéo nhau DC và SB.
?. Cách chứng minh hai mặt phẳng vuông góc.
?. Cách xác định góc giữa đường thẳng và mặt phẳng.
Bài 4. Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a và cạnh bên bằng 2a.
	a. Chứng minh rằng hai mặt phẳng (SAC) và (SBD) vuông góc với nhau.
	b. Tính gần đúng (độ, phút, giây) số đo góc giữa hai mặt phẳng (SBC) và (ABCD).
	c. Tính khoảng cách từ trung điểm J của AD đến mặt phẳng (SBC).
III. Củng cố:
	Gọi học sinh nhắc lại các kết quả cần nhớ như diện tích, độ dài đường cao trong tam giác đều,  , diện tích, độ dài đường chéo hình vuông.