Giáo án Toán lớp 12 dạy hè

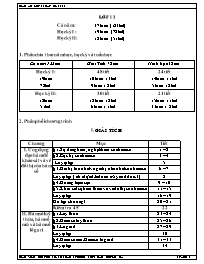
Líp 12
Cả năm : 	37 tuần (123 tiết)
Học kỳ I : 	19 tuần (72 tiết)
Học kỳ II: 	18 tuần (51 tiết)
1. Phân chia theo năm học, học kỳ và tuần học
Cả năm 123 tiết
Giải Tích 78 tiết
Hình học 45 tiết
Học kỳ I:
19 tuần
72 tiết
48 tiết
10 tuần x 3tiết
9 tuần x 2tiết
24 tiết
14 tuần x 1tiết
5 tuần x 2tiết 
Học kỳ II:
18 tuần
51 tiết
30 tiết
12 tuần x 2tiết
6 tuần x 1tiết
21 tiết
15 tuần x 1tiết
3 tuần x 2tiết
2. Phân phối chương trình
I. gi¶I tÝch
Chương
Mục
Tiết
I. Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số
§1. Sự đồng biến, nghịch biến của hàm số 
1 – 2
§2. Cực trị của hàm số
3 – 4
 Luyện tập
5
§3. Giá trị lớn nhất và giá trị nhỏ nhất của hàm số
6 – 7
Luyện tập ( cã thùc hµnh trên m¸y tÝnh bá tói )
8
§4. Đường tiệm cận
9 – 10
§5. Khảo sát sự biến thiên và vẽ đồ thị của hàm số
11 – 15
Luyện tập
16 – 19
Ôn tập chương I
20 – 21
Kiểm tra 45’
22
II. Hàm số luỹ thừa, hàm số mũ và hàm số lôgarit
§1. Luỹ thừa
23 – 24
§2. Hàm số lũy thừa
25 – 26
§3. Lôgarit
27 – 29
Luyện tập
30
§4. Hàm số mũ. Hàm số lôgarit
31 – 33
Luyện tập
34
§5. Phương trình mũ và phương trình lôgarit. 
35 – 36
Luyện tập ( có thực hành trên máy tính bỏ túi )
37 – 38
Kiểm tra 45’
39
§6. Bất phương trình mũ và lôgarit
40 – 41
Ôn Tập
42
Kiểm tra học kỳ I
43
Trả bài kiểm tra cuối học kỳ I
44
Tổng ôn tập cho thi tốt nghiệp
45 – 48
III. Nguyên hàm, tích phân và ứng dụng
§1. Nguyên hàm. Luyện tập
49 – 52
§2. Tích phân
53 – 55
Luyện tập
56 – 57
Kiểm tra 45’
58
§3. Ứng dụng của tích phân trong hình học
59 – 61
Ôn tập chương III
62
IV. Số phức
§1. Số phức. Luyện Tập
63
§2. Cộng, trừ và nhân số phức
64
Luyện Tập
65
§3. Phép chia số phức
66
 Luyện Tập
67
Kiểm tra 45’
68
§4. Phương trình bậc hai với hệ số thực
69
 Luyện Tập
70
Ôn tập cuối năm
71 – 72
Kiểm tra cuối năm
73
Trả bài kiểm tra cuối năm
74
Tổng ôn tập cho thi tốt nghiệp
75 - 78
II. h×nh häc
Chương
Mục
Tiết
I. Khối đa diện
§1. Khái niệm về khối đa diện 
1 – 3
§2. Khối đa diện lồi và khối đa diện đều
4 – 6
§3. Khái niệm về thể tích của khối đa diện. 
7 – 9
Ôn tập chương I
10 – 11
Kiểm tra 45’ 
12
II. Mặt nón, mặt trụ, mặt cầu
§1. Khái niệm về mặt tròn xoay
13 – 15
§2. Mặt cầu
16 – 18
Ôn tập chương II
19 – 20
Kiểm tra học kỳ I
21
Trả bài kiểm tra cuối học kỳ I
22
Tổng ôn tập cho thi tốt nghiệp
23 – 24
Ôn tập chương II ( tiếp theo )
25 – 26
III. Phương pháp toạ độ trong không gian
§1. Hệ toạ độ trong không gian
27 – 29
§2. Phương trình mặt phẳng
30 – 32
Luyện Tập
33
Kiểm tra 45’
34
§3. Phương trình đường thẳng trong không gian
35 – 37 
Luyện Tập
38
Ôn tập chương III
39
Ôn tập cuối năm
40 – 41
Kiểm tra cuối năm
42
Trả bài kiểm tra cuối năm
43
Tổng ôn tập cho thi tốt nghiệp
44 – 45
Tổ trưởng chuyên môn
Hiệu trưởng
( ký tên và đóng dấu)
1.SỰ ĐỒNG BIẾN, NGHỊCH BIẾN CỦA HÀM SỐ
I-TÍNH ĐƠN ĐIỆU CỦA HÀM SỐ
1.Nhắc lại định nghĩa
	Kí hiệu K là khoảng, hoặc đoạn hoặc nửa khoảng. Giả sử hàm số y = f(x) xác định trên K. Ta nói : Hàm số y = f(x) đồng biến (tăng) trên K nếu với mọi cặp x1, x2 thuộc K mà x1 nhỏ hơn x2 thì f(x1) nhỏ hơn f(x2), tức là : 
x1 f(x1) < f(x2);
Hàm số y = f(x) nghịch biến (giảm) trên K nếu với mọi cặp x1, x2 thuộc K mà x1 nhỏ hơn x2 thì f(x1) lớn hơn f(x2), tức là :
x1 f(x1) > f(x2);
Hàm số đồng biến hoặc nghịch biến trên K được gọi chung là hàm số đơn điệu trên K
NHẬN XÉT : Từ định nghĩa trên, ta thấy :
f(x) đồng biến trên K > 0 , x1 ,x2 K (x1 x2)
f(x) nghịch biến trên K < 0 , x1 ,x2 K (x1 x2)
Nếu hàm số đồng biến trên K thì đồ thị đi lên từ trái sang phải (H.3a)
Nếu hàm số nghịch biến trên K thì đồ thị đi xuống từ trái sang phải (H.3b)
2.Tính đơn điệu và dấu của đạo hàm
Ta thừa nhận định lý sau đây :
ĐỊNH LÝ : Cho hàm số y = f(x) có đạo hàm trên K
Nếu f’(x)>0 với mọi x thuộc K thì hàm số f(x) đồng biến trên K
Nếu f’(x)< 0 với mọi x thuộc K thì hàm số f(x) nghịch biến trên K
Tóm lại , trên K:
f’(x) > 0 => f(x) đồng biến
f’(x) f(x) nghịch biến
Chú ý :
Nếu f’(x) = 0, thì f(x) không đổi trên K
Ví dụ 1: Tìm các khoảng đơn điệu của hàm số
y = 2x4 + 1
y = sinx trên khoảng (0; 2)
Giải
Hàm số đã cho xác định với x R
Ta có y’= 8 x3 
Bảng biến thiên:
x
	0	
y’
 	-	 0	+
y
 1
Vậy hàm số y = 2x4 + 1 nghịch biến trên (, 0), đồng biến trên (0, )
b)Xét trên khoảng (0; 2), ta có y’(x) = cos x
Bảng biến thiên :
x
0	/2	3/2	2
y’
 	+	0	 -	0	+
y
 1 	 0
0	-1
Vậy hàm số y = sinx đồng biến trên các khoảng (0; /2) và (3/2; 2), nghịch biến trên khoàng (/2 ; 3/2)
CHÚ Ý : Ta có định lý mở rộng sau:
Giả sử hàm số y =f(x) có đạo hàm trên K.Nếu f’(x) 0 (f’(x) 0), x K và f’(x) = 0 chỉ tại một số hữu hạn điểm thì hàm số đồng biến (nghịch biến) trên K.
Ví dụ 2 :Tìm các khoảng đơn điệu của hàm số y = 2 x3 + 6x2 + 6x -7
Giải
Hàm số đã cho xác định với x R
Ta có y’=6x2 + 12x + 6 = 6(x+1)2
Do đó , y’ =0 x = -1 và y’ > 0 với x -ý 
Theo định lý mở rộng, hàm số đã cho luôn luôn đồng biến 
II.QUY TẮC XÉT TÍNH ĐƠN ĐIỆU CỦA HÀM SỐ
QUY TẮC
Tìm tập xác định
Tính đạo hàm f’(x). Tìm các điểm xi ( i = 1, 2, , n) mà tại đó đạo hàm bằng 0 hoặc không xác định
Sắp xếp các điểm xi theo thứ tự tăng dần và lập bảng biến thiên 
Nêu kết luận về các khoảng đồng biến , nghịch biến của hàm số
ÁP DỤNG
Ví dụ 3 : Xét sự đồng biến, nghịch biến của hàm số
y = x3- x2 – 2x + 2
Giải
Hàm số xác định với mọi x R . Ta có : y’ = x2 – x – 2 , y’=0 
Bảng biến thiên :
x
	-1	 2	
y’
 	+	0	 -	0	+
y
Vậy hàm số đồng biến trên các khoảng (; -1) và (2; ), nghịch biến trên khoảng (-1;2).
Ví dụ 4 : Tìm các khoảng đơn điệu của hàm số y = 
Giải
Hàm số xác định với x -1.
Ta có : y’ = = ; y’ không xác định tại x = -1
Bảng biến thiên :
x
	-1	
y’
 	+	 	+
y
 	 1
1	 
Ví dụ 5 : Chứng minh rằng x > sinx trên khoảng (0 ; ) bằng cách xét khoảng đơn điệu của hàm số f(x) = x – sinx.
Giải
 Xét hàm số f(x) = x – sinx (0 x < ), ta có : f’(x) = 1 – cos x 0 (f’(x) = 0 chỉ tại x = 0) nên theo chú ý trên ta có f(x) đồng biến trên nửa khoảng .
Do đó, với 0 f(0) = 0 hay x > sinx trên khoảng .
Bài tập đề nghị:
1/ Xét chiều biến thiên của các hàm số:
a) y = 4 + 3x – x2 b) y = 2x3 + 3x2 + 1 c) y = d) y = x3 - 2x2 + x + 1 e) y = - x3 + x2 – 5 f) y = x3 – 3x2 + 3x + 1 g) y = - x3 – 3x + 2 h) y = x4 – 2x2 + 3 k) y = - x4 + 2x2 – 1 l) y = x4 + x2 – 1 m) y = n) y = 
p) y = x + q) y = x - r) y = 
2/ Tìm m để các hàm số sau đồng biến trên tập xác định.
y = x3 -3mx2 + (m + 2)x – 1 ĐS: 
y = mx3 – (2m – 1)x2 + 4m -1 ĐS: m = 
3/ Tìm m để các hàm số sau nghịch biến trên tập xác định.
 a) y = - ĐS: 
 b) y = ĐS: m
4. Cho hµm sè y=x3-3(2m+1)x2+(12m+5)x+2. T×m m ®Ó hµm sè lu«n ®ång biÕn.
5. Cho hµm sè y=mx3-(2m-1)x2+(m-2)x-2. T×m m ®Ó hµm sè lu«n ®ång biÕn.
2. CỰC TRỊ CỦA HÀM SỐ
I- KHÁI NIỆM CỰC ĐẠI , CỰC TIỂU
ĐỊNH NGHĨA
Cho hàm số y = f(x) xác định và liên tục trên khoảng (a;b)(có thể a là ; b là )
và điểm x0 (a; b).
Nếu tồn tại số h > 0 sao cho f(x) < f(x0) với x (x0 –h ; x0 + h) và x x0 thì ta nói hàm số f(x) đạt cực đại tại x0
Nếu tồn tại số h > 0 sao cho f(x) > f(x0) với x (x0 –h ; x0 + h) và x x0 thì ta nói hàm số f(x) đạt cực tiểu tại x0.
CHÚ Ý 
Nếu hàm số f(x) đạt cực đại (cực tiểu) tại x0 thì x0 được gọi là điểm cực đại(điểm cực tiểu ) của hàm số; f(x0) được gọi là giá trị cực đại (giá trị cực tiểu) của hàm số, ký hiệu là fCĐ , (fCT) , còn điểm M(x0, f(x0)) được gọi là điểm cực đại (điểm cực tiểu) của đồ thị hàm số .
Các điểm cực đại và cực tiểu được gọi chung là điểm cực trị. Giá trị cực đại (giá trị cực tiểu) còn gọi là cực đại (cực tiểu) và được gọi chung là cực trị của hàm số.
Dễ dàng chứng minh được rằng, nếu hàm số y = f(x) có đạo hàm trên khoảng (a ; b) và đạt cực đại hoặc cực tiểu tại x thì f’(x0) = 0.
II- ĐIỀU KIỆN ĐỦ ĐỂ HÀM SỐ CÓ CỰC TRỊ
Ta thừa nhận định lý sau :
Định lí 1 :
Giả sử hàm số y= f(x) liên tục trên khoảng K = (x0 – h ; x0 + h) và có đạo hàm trên K hoặc trên K \{ x0 } , với h > 0.
Nếu f’(x) > 0 trên khoảng (x0 – h ; x0 ) và f’(x) < 0 trên khoảng (x0 ; x0 + h) thì x0 là một điểm cực đại của hàm số f(x).
Nếu f’(x) 0 trên khoảng (x0 ; x0 + h) thì x0 là một điểm cực tiểu của hàm số f(x).
x
x0 – h 	x0 	x0 + h
f’(x)
	+	-
f(x)
fCĐ
x
x0 – h 	x0 	x0 + h
f’(x)
	-	+
f(x)
fCT
Ví dụ 1:
 	Tìm các điểm cực trị của đồ thị hàm số f(x) = - x2 + 1
Giải
Hàm số xác định với x R .
Ta có : f’(x) = -2x ; f’(x) =0 x=0 
Bảng biến thiên: 
x
	0	
f’(x)
 	+ 	 0	-
f(x)
 1 	
Từ bảng biến thiên suy ra x= 0 là điểm cực đại của hàm số và đồ thị của hàm số có một điểm cực đại (0; 1).
Ví dụ 2 :
Tìm các điểm cực trị của hàm số y = x3 – x2 –x + 3
Giải
Hàm số xác định với x R .
 Ta có : y’ = 3x2 – 2x -1 ; y’ =0 
Bảng biến thiên:
x
	-1/3	 1	 
y’
 	+	0	 -	0	+
y
 	2
Từ bảng biến thiên suy ra x = -1/3 là điểm cực đại , x= 1 là điểm cực tiểu của hàm số đã cho.
Ví dụ 3 : Tìm cực trị của hàm số :
 y = 
Giải
Hàm số xác định tại x -1 
Ta có y’ = > 0 , x -1
Vậy hàm số đã cho không có cực trị (vì theo khẳng định 3 của chú ý trên, nếu hàm số có cực trị tại x0 thì tại đó y’ = 0 ) .
III- QUY TẮC TÌM CỰC TRỊ
Áp dụng Định lý 1, ta có quy tắc tìm cực trị sau đây :
QUY TẮC 1 : 
Tìm tập xác định.
Tính f’(x) . Tìm các điểm tại đó f’(x ) bằng 0 hoặc f’(x) không xác định
Lập bảng biến thiên
Từ bảng biến thiên suy ra các điểm cực trị.
Ta thừa nhận định lý sau : 
ĐỊNH LÍ 2 :
Giả sử hàm số y =f(x) có đạo hàm cấp 2 trong khoảng (x0 – h ; x0 + h), với h > 0. Khi đó :
Nếu f’(x0 ) = 0, f”( x0 ) > 0 thì x0 là điểm cực tiểu
Nếu f’(x0 ) = 0, f”( x0 ) < 0 thì x0 là điểm cực đại
Áp dụng định lý 2 , ta có quy tắc sau đây để tìm các điểm cực trị của một hàm số
QUY TẮC II
Tìm tập xác định
Tính f’(x). Giải phương trình f’(x) =0 và ký hiệu xi ( i =1,2,.) là các nghiệm của nó.
Tính f”(x) và f”(xi)
Dựa vào dấu của f”( xi) suy ra tính chất cực trị của điểm xi
Ví dụ 4 : Tìm cực trị của hàm số
f(x) = - 2 x2 + 6
Giải
Hàm số xác định với x R .
f’(x) = x3 - 4x =x(x 2 – 4) 
f’(x) = 0 x1 = 0 ; x2 = -2 ; x3 =2
f”(x) =3 x 2 – 4
f”( 2) = 8 > 0 x = -2 và x =2 là hai điểm cực tiểu.
f”(0) = -4 < 0 x =0 là điểm cực đại.
Kết luận :
f(x) đạt cực tiểu tại x = -2 và x = 2 , f CT = f( 2) =2.
f(x) đạt cực đại tại x =0 và fCĐ = f(0) = 6
Ví dụ 5 : Tìm các điểm cực trị của hàm số f(x) = sin 2x
Giải
Hàm số xác định với x R .
f’(x) = 2 cos2x.
f’(x )=0 2x = + l x = + l (l Z).
f”(x) = -4 sin 2x.
f”( + l ) = -4 sin( + l) = - 4 nếu l = 2k
 = 4 nếu l = 2k + 1(k Z).
Kết luận:
x = + k( kZ) là các điểm cực đại của hàm số.
x = + k( kZ) là các điểm cực tiểu của hàm số.
Bài tập đề nghị:
1. Tìm cực trị của các hàm só.
1) y = x2 – 3x – 4 ;	2) y = -x2 + 4x – 3 ;	3) y = 2x3 -3x2 + 1 ;	
4) y = ;	5) y = -2x3 + 3x2 + 12x – 5 ;	6) y = x3 – 3x2 + 3x + 1 ;	
7) y = -x3 -3x + 2 ;	8) y = 	9) y = ;
10) y = x4 + 2x2 + 2 ;	11) y = ;	12) y = ;	13) y = 1 - ; 
14) y = ;	15) y = 	;	16) y = ;	17) y = ;
2. Định m để y= đạt cực đại tại x=1. 
3. Cho hàm số y= . Định a,b để hàm số đạt cực trị bằng –2 tại x=1. 
4. Tìm m để các ... y
 + ¥ 
 a
 1 
0
 4. Đồ thị: (SGK, trang 73)
 a > 1
 y = ax
1. Tập xác định: R
2. Sự biến thiên:
 y’ = (ax)’ = axlna < 0 " x.
 Giới hạn đặc biệt : 
 ; 
 Tiệm cận: trục Ox là tiệm cận ngang.
3. Bảng biến thiên:
x
- ¥ 0 1 + ¥
y’
 +
y
+ ¥ 
 1 
 a 
 0 
 4. Đồ thị: (SGK, trang 73)
0 < a < 1
 y = ax
 Bảng tóm tắt các tính chất của hàm số mũ: y = ax (a > 0, a ¹ 1):
Tập xác định
(- ¥; + ¥)
Đạo hàm
y’ = (ax)’ = axlna
Chiều biến thiên
a > 1: hàm số luôn đồng biến.
0 < a < 1: hàm số luôn nghịch biến.
Tiệm cận
Trục Ox là tiệm cận ngang.
Đồ thị
Đi qua điểm (0; 1) và (1; a), nằm phía trên trục hoành.
(y = ax > 0, " x. Î R.
II. HÀM SỐ LÔGARIT
1. Định nghĩa: Cho số thực dương a khác 1. Hàm số y = logax được gọi là hàm số lôgarit cơ số a.
2. Đạo hàm của hàm số lôgarit
Định lý 3 :
 Hàm số : y = logax (a > 0, a1) có đạo hàm tại mọi x > 0 và: (logax)’ = .
Đặc biệt: (lnx)’ = .
Đối với hàm số hợp, ta có : (logau)’ = 
Hoạt động 3 :
 Tìm đạo hàm của hàm số: 
y’=
 = .
3. Khảo sát hàm số lôgarit: 
Bảng khảo sát hàm số y = logax ( a> 0 ; a0)
logax, a > 1
logax, 0 < a < 1
1. Tập xác định: (0; + ¥)
2. Sự biến thiên:
y’ = (logax)’ = > 0 " x. > 0
 Giới hạn đặc biệt : 
 ; 
 Tiệm cận: trục Oy là tiệm cận đứng.
3. Bảng biến thiên:
x
0 1 a + ¥
y’
 +
y
 + ¥ 
 1
 0 
- ¥
 4. Đồ thị: (SGK, trang 76)
1. Tập xác định: (0; + ¥)
2. Sự biến thiên:
y’ = (logax)’ = 0
 Giới hạn đặc biệt : 
 ; 
 Tiệm cận: trục Oy là tiệm cận đứng.
3. Bảng biến thiên:
x
0 a 1 + ¥
y’
 +
y
+ ¥ 
 1 
 0 
 - ¥ 
 4. Đồ thị: (SGK, trang 76)
§ PHƯƠNG TRÌNH MŨ VÀ PHƯƠNG TRÌNH LÔGARIT
I. PHƯƠNG TRÌNH MŨ.
Bài toán: SGK
1-Phương trình mũ cơ bản.
 Phương trình mũ cơ bản có dạng 
 ax = b (a > 0, a ¹ 1)
+ Với b > 0: ta có, ax = b Û x = loga b.
+ Với b £ 0 : ta có phương trình vô nghiệm.
Minh họa bằng đồ thị
VD1 : Giải phương trình 22x-1+4x+1 = 5
Đưa về cùng cơ số 4 ta được
2.Cách giải một số phương trình mũ cơ bản :
a/ Đưa về cùng cơ số.
HĐ1: Giải phương trình sau: 6 2x – 3 = 1 (1)
Ta có 6 2x – 3 = 60 
VD2: 
 b/ Đặt ẩn phụ:
VD3: giải phương trình 9x – 5.3x – 6 = 0
Giải. Đặt t = 3x, t > 0, ta có phương trình
 t2 – 5t – 6 = 0
với t = 6 có 3x = 6 Û x = log36
HĐ2: Giải phương trình .52x + 5.5x = 250. 
Giải: Đặt t = 5x (t > 0) ta có
Û 5x = 25x = log 5 25 = 2
c/ Logarit hoá:
VD4 : giải phương trình 
Lấy lôgarit cơ số 3 hai vế ta được
Û x +x2 log32 = 0 Û x(1+xlog32)= 0
Phương trình có nghiệm x = 0 và x = - log23
II. PHƯƠNG TRÌNH LOGARIT.
Phương trình logarit là phương trình có chứa ẩn số trong biểu thức dưới dấu lôgarit.
Ví dụ: ; 
1. Phương trình logarit cơ bản:
HĐ3: Tìm x biết 
Giải : 
Phương trình logarit cơ bản có dạng: logax = b (a >0 , a 1 )
Phương trình luôn có nghiệm duy nhất x = ab
Minh hoạ bằng đồ thị H39, H40 
2. Cách giải một số phương trình lôgarit đơn giản
a/ Đưa về cùng cơ số.
HĐ4: 
 VD5: Giải pt log3x + log9x + log27x = 11
Kq: x = 36 = 729 
b/ Đặt ẩn phụ:
HĐ6:
Đ/s :x = 2-1= ; x = 4
VD6 : Giải phương trình 
Giải. Điều kiện x > 0, 
Đặt t = log x ( t5, t1) được 
Û t = 2, t = 3 cả 2 thỏa điều kiện
Û x = 100 và x = 1000
c. Mũ hóa 
VD7 : Giải pt log 2(5 – 2x ) = 2 – x (*)
Điều kiện 5 – 2x > 0
(*) Û Û 
Û 22x-5.2x +4 = 0 . Đặt t = 2x (t > 0), ta có pt 
t2 – 5t + 4 = 0 Û t = 1 v t = 4 Û x = 0, x = 2
§‘ BẤT PHƯƠNG TRÌNH MŨ VÀ BẤT PHƯƠNG TRÌNH LÔGARIT
I. BẤT PHƯƠNG TRÌNH MŨ.
 1. Bất phương trình mũ cơ bản:
“Bất phương trình mũ cơ bản có dạng ax > b (hoặc ax ³ b, ax 0, a ¹ 1)”
 Ta xét bất phương trình dạng: ax > b 
+ Nếu b £ 0 ta có ax >0 ³ b với " x Î R nên tập nghiệm R
+ Nếu b > 0 ta có ax > b Û ax > (*)
Với a >1 thì (*) Û x > loga b
Với 0 < a < 1 thì (*) Û x < loga b.
2. Bất phương trình mũ đơn giản :
VD2: Giải bất phương trình 
(vì)
Vậy tập nghiệm là đoạn [-3; 1].
VD3: Giải bpt 4x – 2.52x < 10x 
KQ: 
HĐ2: Giải bpt 2x +21–x – 3 < 0
Đặt t = 2x (t>0), Ta được 
 ( vì t > 0) 
Tập nghiệm là khoảng ( 0; 1)
II. BẤT PHƯƠNG TRÌNH LÔGARIT
1. Bất phương trình lôgarit cơ bản :
“Bất phương trình lôgarit cơ bản có dạng logax > b (hoặc logax ³ b, logax 0,a ¹ 1”
 Ta xét bất phương trình logax > b (**):
a > 1
0 < a < 1
(**) Û x > ab
	(**) Û 0 < x < ab
VD4: 
log2 x >7 Û x > 27 Û x > 128.
2. Bất phương trình logarit đơn giản :
VD5: Giải bpt 
Vậy tập nghiệm là khoảng ( - 2 ; 1)
VD6: Giải bpt 
Vậy tập nghiệm của bpt là (3; 4].
HĐ4 : Giải bpt (***)
Vì <1 nên (***) tương đương với
Tài liệu của học sinh: ....................................................................................
CHƯƠNG II
HÀM SỐ LŨY THỪA, HÀM SỐ MŨ, HÀM SỐ LÔGARIT
§Œ LUỸ THỪA
1. Tính chất của luỹ thừa với số mũ nguyên dương. 
 "a, b Î R+, m, nÎ R. Ta có: 
 i) am.an = am+n
 ii) 
 iii) 
 iv) (a.b)n = an.bn. 
 v) 
 vi) 0 < a < b 
 vii) 
 viii) .
2. Tính chất của căn bậc n:
3. Tính chất của luỹ thừa với số mũ thực. 
Cho a, b > 0 ; là những số thực tùy ý. Khi đó ta có:
§Ž LÔGARIT
1. §Þnh nghÜa:Víi a > 0 , a 1 vµ N > 0 ta cã: 	 
 Chó ý: §iÒu kiÖn cã nghÜa: cã nghÜa khi . 
2. C¸c tÝnh chÊt 
+ 
+ 
+ 
+ 
+ 
+ 
+ , ®b: 
3. C«ng thøc ®æi c¬ sè 
+ +
 * C«ng thøc ®Æc biÖt: 
* HÖ qu¶: + 
 + 
HÀM SỐ LŨY THỪA, HÀM SỐ MŨ, HÀM SỐ LÔGARIT
1. Hàm số lũy thừa :
 Dạng : y = xa, với a Î R.
* Chú ý :
 + Với a nguyên dương, tập xác định là R.
 + Với a nguyên âm hoặc bằng 0, tập xác định là R\{0}
 + Với a không nguyên, TXĐ D = (0; + ¥)
(x a)’ = a x a - 1
y = xa (a > 0)
y = xa (a < 0)
1.Tập khảo sát: (0 ;+¥)
2. Sự biến thiên : 
 y’ = ax a - 1 > 0,"x> 0.
 Giới hạn đặc biệt :
; 
 Tiệm cận: không có.
3. Bảng biến thiên:
x
0 + ¥
y’
 + 
y
 + ¥ 
0
1.Tập khảo sát : (0 ;+¥)
2. Sự biến thiên : 
y’ = ax a - 1 0.
 Giới hạn đặc biệt :
; 
TCN: y = 0
TCĐ: x = 0
3. Bảng biến thiên:
x
0 + ¥
y’
 -
y
+ ¥ 
 0
4. Đồ thị 
* Chú ý :
 + Đồ thị của hàm số y = xa luôn đi qua điểm (1 ; 1)
 + Khi khảo sát hàm số luỹ thừa với số mũ cụ thể, ta phải xét hàm số đó trên toàn bộ tập xác định của nó.
2. Hµm sè mò: 
D¹ng : ( a > 0 , a1 ).
- TËp x¸c ®Þnh : 
- TËp gi¸ trÞ : ()
- TÝnh ®¬n ®iÖu:
* a > 1 ®ång biÕn trªn 
* 0 < a < 1 nghÞch biÕn trªn . 
- §å thÞ hµm sè mò :
 a>1
 y =ax
 0<a<1
 y=ax
3. Hµm sè logarÝt: 
D¹ng: ( a > 0 , a 1 ).
- TËp x¸c ®Þnh : 
- TËp gi¸ trÞ 
- TÝnh ®¬n ®iÖu: 
* a > 1 ®ång biÕn trªn 
* 0 < a < 1 nghÞch biÕn trªn 
- §å thÞ cña hµm sè l«garÝt:
BÀI TẬP CỦA HỌC SINH:.......................................................................................
I. LUỸ THỪA – HÀM SỐ MŨ:
1.Rút gọn các biểu thức sau:
a) 
b) 
c) ( )– 10.27 – 3 + (0,2)– 4.25– 2 
d) 
e) – 
f)(x.a–1 – a.x –1). – 
	2.Tính các biểu thức sau:
a) 
b) 
c) 
d)
e) 
f) g) 
g) 
h) 
l) 
3.Cho hai số a ,b > 0.Tính các biểu thức sau:
a) 
b) 
c) 
d) 
e) 
f) 
g) 
h) 
i) 
4.Rút gọn các biểu thức sau:
 a)A = 
b) B = 
c) C = 
d) D = 
e) E = 
f) F = 
g)G = 
h) : 
5.Cho biết 9x + 9– x = 23 ,hãy tính 3x + 3– x
6.Cho f(x) = Chứng minh rằng nếu a + b = 1 thì f(a) + f(b) = 1
II. HÀM SỐ LÔGARIT: 
1.Tính
 ; 	 ; 	 ; 	 ; 	log3(log28) ; 	 ; ; 	 ;	 ; 	 ; 	 ; 	( 
2. Chứng minh rằng ; .
3.Rút gọn các biểu thức sau:
a) 	b) 	c) 
d) 	f) 
4.Cho log23 = a ; log25 = b.
Tính các số sau: log2,log2, log2180, log3, log1524, 
5. a)Cho log53 = a, tính log2515	b) Cho log96 = a , tính log1832
6.Cho log2 = a , log27 = b,tính log56.
7.Cho log615 = a ,log1218 = b , tính log2524.
8.Cho log257 = a ,log25 = b hãy tính .
9. Chứng minh rằng log186 + log26 = 2log186.log26
10.Cho a2 + b2 = 7ab a > 0, b > 0,chứng minh rằng : log7() = ( log7 a + log7b )
11.Cho a2 + 4b2 = 12ab a > 0, b > 0,chứng minh rằng: log(a + 2b) – 2log2 = ( loga + logb )
12.Cho x2 + 4y2 = 12xy x > 0,y > 0, Chứng minh rằng log3(x + 2y) – 2log32 = (log2x + log2y).
13.Cho log1218 = a , log2454 = b ,chứng minh rằng ab + 5(a – b) = 1
14.So sánh các cặp số sau:
a) log43 và log56 	 b) và 	c) log54 và log45 	d) log231 và log527 
e) log59 và log311 f) log710 và log512 
15.Tìm miền xác định của các hàm số sau:
a)y = log6 	b) y = 	c) y = 
III. Đạo hàm của hàm luỹ thừa – hàm số mũ – hàm số lôgarit:
Tính đạo hàm của các hàm số sau:
1. y = (5x2 – 4)ln3x
2. y = . lnx6
3. y = (x + 2) ln
4. y = 
5. y = 
6. y = 
7. y = 
8. y = 
9. y = 
10. y = x2 
11. y = (x2 + 2) e2x
12. y = xlnx - xln5
13. y = xlnx – xln2
14. y = (x2 – 2x + 2)ex
15. y = (sinx – cosx) e2x
16. y = 2x - 
17. y = (3x + 1) e
§ PHƯƠNG TRÌNH MŨ VÀ PHƯƠNG TRÌNH LÔGARIT
1. Phương trình mũ:
a. Dạng cơ bản: 	 
+ 
+ 
b. Dạng có số có chứa ẩn: 
 Chú ý: Một số phương pháp thường dùng khi giải phương trình mũ
C1: Đưa về phương trình dạng cơ bản
C2: Lấy lôgarit hai vế khi 2 vế của pt có dạng tích hoặc thương
C3: Đặt ẩn phụ (chú ý điều kiện của ẩn phụ)
Biến đổi phương trình về dạng	 
- Dạng 1: a. +b. + g = 0 , Đặt t = Đ/K t > 0
- Dạng 2: a.+b.+ g = 0, Đặt t = Đ/K t > 0
- Dạng 3: a.+b.+ g = 0 với a.b = 1, Đặt t = =
- Dạng 4: a.+b.+ g. = 0 , Chia 2 vế cho và đặt t = , t>0
C4: Đánh giá: Dùng BĐT, hàm số, đoán nghiệm và chứng minh nghiệm duy nhất,.. (thường thì PT có 1 nghiệm duy nhất) 
2. Phương trình logarit
a. Dạng cơ bản: 	 
 + 
+ 
b. Cơ số có chứa ẩn: 
 Chú ý: Một số phương pháp thường dùng khi giải phương trình logarit
C1: Đưa về cùng cơ số
C2: Mũ hoá
C3: Đặt ẩn phụ 
C4: Đáng giá: Dùng BĐT, Hàm số, đoán nghiệm và chứng minh nghiệm duy nhất,... 
§‘ BẤT PHƯƠNG TRÌNH MŨ VÀ BẤT PHƯƠNG TRÌNH LÔGARIT
- Về cơ bản thì phương trình mũ và logarit có các cách giải nào thì bất phương trình mũ và logarit có các cách giải đó
- Một số kiến thức cần nhớ
+ 

+
- Chú ý: Các phương pháp thường dùng khi giải bất phương trình mũ và logarit giống như giải phương trình mũ và logarit với lưu ý chiều của bất phương trình khi thực hiện biến đổi.
IV. PHÖÔNG TRÌNH MUÕ:
1. 
2. 33x – 1 = 9x + 2
3. 
4.
5. 4x = 82x – 1
6. 34 – 2x = 
7. 
8. = 252x – 4
9. = 92x – 2
10. 
11. = 36. 32 –x 
12. 5x . = 50
13. 3x . = 36
14. 3x-1 . = 8. 4x - 2
15. 52x-1+5x+1 - 250 = 0 
16. 9x + 6x = 2.4x 
17. 22x-3 - 3.2x-2 + 1 = 0 18. 
19. 
20. = 12.
21. 
22. 	
23. 
24. 
25. 
26. 7. 3x+1 - 5x+2 = 3x+4 - 5x+3 
27. 6. 4x - 13.6x + 6.9x = 0 
28. 76-x = x + 2
29. 
30. 
31. 3x+1 + 3x-2 - 3x-3 + 3x-4 = 750 
32. 3.25x-2 + (3x - 10)5x-2 + 3 - x = 0 
33. 5x + 5x +1 + 5x + 2 = 3x + 3x + 3 - 3x +11 
34. 3x+3x+1+3x+2=5x+5x+1+5x+2 
35. 2x+2x-1+2x-2=7x+7x-1+7x-2 
36. 
37. 
38. 
39. 
40. 
41. 
42. 
V. PHÖÔNG TRÌNH LOÂGARIT:
1. 
2. 
3. 	 
4.
5.
6.	
7.	
8. 
9. 1/
10/. 	
11/. 
12/. 
13/. 
14/. 	
15/. 
16/. 
18/. 22x-3 - 3.2x-2 + 1 = 0 
19/. 
20/. = 12.
21/. 
22/. 	
23/. 
24/. 
25/. 
26/. 7. 3x+1 - 5x+2 = 3x+4 - 5x+3 
27/. 6. 4x - 13.6x + 6.9x = 0 
28/. 	16/. 
29/. 
30/.