Giáo án Tiết 20: Kiểm tra chương 1

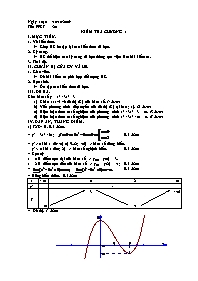
Ngày soạn	:10/10/2009
Tiết PPCT	:20
KIỂM TRA CHƯƠNG 1
I. MỤC TIÊU.
1. Về kiến thức.
Giúp HS ôn tập lại các kiến thức đã học.
2. Kỹ năng.
HS thể hiện các kỹ năng đã học thông qua việc làm bài kiểm tra.
3. Thái độ.
II. CHUẨN BỊ CỦA GV VÀ HS.
1. Giáo viên.
Đề bài kiểm tra phù hợp đối tượng HS.
2. Học sinh.
Ôn tập các kiến thức đã học.
III. ĐỀ RA.
Cho hàm số y = x3 - 3x2 +3
Khảo sát và vẽ đồ thị (C) của hàm số. (4 điểm)
Viết phương trình tiếp tuyến của đồ thị (C) tại M(1; 1). (2 điểm)
Biện luận theo m số nghiệm của phương trình x3 - 3x2 +3 = m. (3 điểm)
Biện luận theo m số nghiệm của phương trình x3 - 3x2 - m = 0. (1 điểm)
IV. ĐÁP ÁN, THANG ĐIỂM.
a) TXĐ: R. 0,5 điểm.
* y’ = 3x2 - 6x; 	0,5 điểm
* y' > 0 khi x (-; 0) (2;+) => hàm số đồng biến.
 y’ hàm số nghịch biến.	0,5 điểm
* Cực trị:
x = 0 là điểm cực đại của hàm số => yCĐ = y(0) = 3.
x = 2 là điểm cực tiểu của hàm số => yCT = y(2) = -1;	0,5 điểm
* 	0,5 điểm
* Bảng biến thiên. 0,5 điểm
x
-
0
2
+
y’
+
-
+
y
+
3
-1
-
* Đồ thị. 1 điểm
b) Phương trình tiếp tuyến tại M(1, 1) (C) có dạng
	y - y0 = y’(x0)(x - x0)	0,5 điểm
với y0 = 1; x0 = 1
y’(x0) = y’(1) = -3.	0,5 điểm
Vậy phương trình tiếp tuyến là y - 1 = -3(x - 1) y = -3x + 4.	1 điểm
c) 	- 1< m < 3 thì phương trình có 3 nghiệm phân biệt	1 điểm	
	m = -1 hoặc m = -3 thì phương trình có hai nghiệm.	1 điểm
	m > 3 hoặc m < -1 thì phương trình có một nghiệm.	1 điểm
d) phương trình được viết lại như sau
x3 - 3x2 +3 = m + 3
Đặt k = m + 3 ta có phương trình x3 - 3x2 +3 = k 	0,5 điểm
Tương tự trên ta biện luận theo k suy ra kết quả như sau:
- 4< m < 0 thì phương trình có 3 nghiệm phân biệt	
	m = -4 hoặc m = 0 thì phương trình có hai nghiệm.	
	m > 0 hoặc m < -4 thì phương trình có một nghiệm.	1 điểm.
HẾT