Giáo án lớp 12 môn Hình học - Tiết 9 - Bài tập sự đồng dạng của các khối đa diện

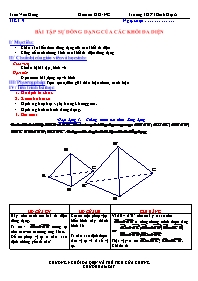
TIẾT: 9’	Ngày soạn: . . . . . . . . . . . . .
 BÀI TẬP SỰ ĐỒNG DẠNG CỦA CÁC KHỐI ĐA DIỆN
I/ Mục tiêu:
Khắc sâu kiến thức đồng dạng của các khối đa diện 
Củng cố cách chứng kinh các khối đa diện đồng dạng 
II/ Chuẩn bị của giáo viên và học sinh:
+ Giáo viên: 
Chuẩn bị bài tập , hình vẽ 
+ Học sinh:
Đọc trước bài ,dụng cụ vẽ hình
III/ Phương pháp: Trực quan,diễn giải thảo luận nhóm, tranh luận
IV/ Tiến trình bài học:
Ổn định tổ chức:
Kiểm tra bài cũ:
Định nghĩa phép vị tự trong không gian.
Định nghĩa hai hình đồng dạng.
Bài mới:
*Hoạt động 1: Chứng minh hai hình đồng dạng
HĐ CỦA GV
HĐ CỦA HS
GHI BẢNG
Hãy nêu cách cm hai đa diện đồng dạng.
Ta có : tương tự cho các véc tơ tương ứng khác.
Để có phép vị tự ta cần xác định những yếu tố nào?
Cm có một phép vịtự biến hình này thành hình kia
Ta cần xác định được tâm vị tự và tỉ số vị tự.
Vì AB// A’B’ nên có k ≠ 0 sao cho
 ta cũng chứng minh được rằng có: 
Thật vậy: ta có ; . Khi đó từ 
Vì không cùng phương nên đẳng thức xảy ra khi và chỉ khi : 
Vây : ;. Tương tự đối với các đẳng thức con lại.
* Khi k = 1 ta có 
Nên ta có phép tịnh tiến theo vectơ biến tứ diện ABCD thành tứ diện A’B’C’D’.
Khi thi hai đường thẳng AA’ va BB’ cắt nhau tại một điểm O. Ta có phép vị tự tâm O tỉ số biến tứ diện ABCD thành tứ diện A’B’C’D’.
Vậy cả hai trường hợp nói trên hai tứ diện ABCD và A’B’C’D’ đồng dạng.
Hoạt động2: Củng cố 
Giải
Gọi V là một phép vị tự tâm O tỉ số k ( O là một diểm bát kì) , là ảnh của tứ diện ABCD qua V. Khi đó . Vậy:
. Do đó tứ diện A’B’C’D’ bằng tứ diện A1B1C1D1, suy ra hai tứ diện ABCD và A’B’C’D’ đồng dạng.
Rút kinh nghiệm
. . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . .. . . . . . . .. . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 
. . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . .. . . . . . . .. . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .