Giáo án Giải tích lớp 12 tiết 21: Ôn tập chương I

Tuần 7 tiết 21
Ngày soạn : ngày dạy :
Bài soạn : ÔN TẬP CHƯƠNG I
I.MỤC TIÊU :
 Tiếp tục rèn luyện dạng toán khảo sát và vẽ đths cũng như giải các bài toán liên quan : Viết pttt của đths , dựa vào đths biện luận số nghiệm của pt .
II.CHUẨN BỊ :
Giáo viên : SGK , thước , phấn màu .
Học sinh : Thước , SGK , xem lại lý thuyết toàn chương I và làm các bài tập đã dặn .
III.THỰC HIỆN TRÊN LỚP :
Ổn định : 
Kiểm tra bài cũ :
Bài mới :
Hoạt động của giáo viên 
Hoạt động của học sinh 
Nội dung 
Hoạt động 1 : Giải bài tập 9 trang 46 SGK .
-Gv nêu đề bài tập 9 cho HS tự giải bằng hoạt động cá nhân câu a . GV theo dõi quan sát và hỗ trợ khi cần thiết .
+Cho HS kiểm tra lẫn nhau kết quả của câu a trước khi tiến hành thảo luận nhóm về trình tự giải câu b .
+Ở câu b thì theo đề bài ta suy ra được gì khi pttt có hoành độ là nghiệm của pt f’’(x) = 0 ?
+Ở câu c thì pt cho có dạng giống với hàm số mà ta vừa khảo sát và vẽ đồ thị không ?Vậy để biện luận theo m số nghiệm của pt thì ta phải làm gì ?
-Tổ chức sửa bài lần lượt theo trình tự các câu nhưng ở câu b và câu c thì huy động mỗi câu 1 HS lên bảng nhưng với câu a thì huy động nhiều HS hơn , đặc biệt tạo điều kiện cho những HS TB , yếu lên bảng trình bày để các em được rèn luyện và tự tin nhiều hơn trong học tập . Qua đó GV uốn nắn , sửa chữa và giúp các em khắc phục những khó khăn , sai lầm trong quá trình giải bài toán khảo sát sự biến thiên và vẽ đồ thị của hàm số .
-Nêu đề bài tập 11a cho HS tự giải bằng hoạt động cá nhân .
-Tổ chức sửa bài tương tự như bài tập 9 . GV cố gắng huy động nhiều HS thực hiện , mỗi em giải 1 bước của bài toán đồng thời tranh thủ xem xét bài giải của các em còn lại , nhất là các đối tượng HS TB , yếu để giúp đỡ , uốn nắn cho các em .
-Giải bài tập như tổ chức của GV .
+Tìm được x0 là nghiệm của pt f’’(x0) = 0 ,từ đó tìm y0 = f(x0) và hsg của tiếp tuyến k = f’(x0) .
+Pt đã cho chưa giống với hàm số mà ta vừa khảo sát và vẽ đồ thị nên phải biến đổi tương đương pt đ4 cho sao cho có 1 vế là hàm số mà taa vừa khảo sát và vẽ đồ thị .
-Tiến hành sửa bài như tổ chức của GV .
-Giải bài tập 11a bằng họt động cá nhân như tổ chúc của GV .
-Trao đổi , thảo luận và sửa bài như tổ chức của GV .
Bài tập 9 trang 46 SGK .
a)y = f(x) = x4 - 3x2 + 
TXĐ : D = R 
y’ = 2x3 – 6x = 2x(x2 – 3 )
 y’ = 0 
f(0) = ; f() = -3
Bảng biến thiên :
x
-∞ - 0 +∞
y’
 - 0 + 0 - 0 +
y
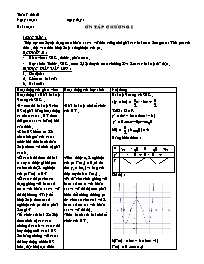
Đồ thị :
b)f’’(x) = 6x2 – 6 = 6(x2 –1)
f’’(x) = 0 x = ±1
f(±1) = -1
Tiếp tuyến tại điểm (1;-1) có pt là y = -4x + 3 . 
Tiếp tuyến tại điểm (-1;-1) có pt là y = 4x + 3 .
c)x4 – 6x2 +3 = m 
x4 - 3x2 + = 
Số nghiệm của pt là số giao điểm của đồ thị các hàm số : 
y = x4 - 3x2 + và y = 
từ đó ta có :
* < 3 hay m < -6 : pt VN .
*=-3 hay m = -6 : pt có 2 nghiệm .
*-3<< hay -6<m<3 : pt có 4 nghiệm .
*= hay m = 3 : pt có 3 nghiệm .
*> hay m>3 : pt có 2 nghiệm .
Bài tập 11 trang 46 SGK .
-TXĐ ; D = R\{-1}
-Sự biến thiên :
y’ = <0 với nên hàm số luôn nghịch biến trên từng khoảng xác định (-∞;-1) và (-1;+∞)
nên đồ thị có tiệm cận đứng x = -1 và tiệm cận ngang y = 1
Bảng biến thiên :
x
-∞ -1 +∞
y’
 - -
y
Đồ thị :
4.Củng cố :
Giải đáp các thắc mắc của HS qua tiết ôn tập .
5.Hướng dẫn học ở nhà :
-Xem lại lý thuyết toàn chương và các bài tập đã giải .
-Chuẩn bị tiết sau làm bài kiểm tra 45 phút .
-Làm các bài tấp còn lại : Bài 10 , 11b,c,d .
	HD bài 11 :
	b) CM pt hoành độ giao điểm của hai hàm số luôn có 2 nghiệm phân biệt .
	c) Sử dụng hệ thức Vi-ét .
	d)Sử dụng công thức tính toạ độ trung điểm của đoạn thẳng AB .