Giáo án Giải tích 12 - Tuần đến tuần 7

Buổi 4
 Ngày dạy: 23/ 10 / 2009.
 Luyện tập 
I/ Mục tiêu:
Rèn kỹ năng khảo sát hàm số trên 2 loại hàm số (đã học), rèn kỹ năng vẽ đồ thị dựa vào bảng biến thiên.
Chứng minh điểm uốn là tâm đối xứng của đồ thị hàm số bậc 3
Phương pháp: HS thể hiện kỹ năng trên bảng.
GV: Nhận xét, góp ý.
II/ Phương tiện
Giáo viên: Giáo án, SGK
Học sinh: Đồ dùng học tập
III/ Phương pháp: Nêu vấn đề phát huy tính tích cực của học sinh+thuyết trình
IV/ Tiến trình bài dạy
ổn định lớp
Kiểm tra bài cũ
HS: Nêu tóm tắt kết quả khảo sát hàm số bậc 3.
Tiến trình bài dạy
Hoạt động của thầy
Hoạt động của trò
Hoạt động1
Bài toán: Cho hàm số y = x3 + 3x + 1,
Có đồ thị (C)
1. Khảo sát HS.
2. Chứng minh rằng: Điểm uốn là tâm đối xứng của (C)
GV-HS: Vẽ đồ thị.
HS: 1. Khảo sát HS.
x
-Ơ
-1
0
1
+Ơ
y'
-
0
+
0
-
y
+Ơ
-1
 1 
3
-Ơ
Lấy A = (-2;3); B(2,1) ở 2 nhánh.
GV: Định lý: y = f(x) là hàm số lẽ nhận gốc O làm tâm đối xứng
Vì I = (0,1) là tâm đối xứng của (C) nên I đóng vai trò là gốc toạ độ của hệ trục khác, mà khi đó hàm số là lẻ.
Công thức đổi trục toạ độ: 
Trên hệ trục XIY (gốc I), hs đã cho có phát triển: y0 + Y = f(x0 + X)
Û Y = f(x0 + X) - y0 = g(X)
I là tâm đối xứng Û Y = g(x) là hàm số lẻ (*)
HS: áp dụng 
1+Y = -(0 + X)3 + 3(0+X) + 1 Û Y = -X3 + 3X = g(x)
Hoạt động của thầy
Hoạt động của trò
Hoạt động1
Bài toán: Cho hàm s ố có đồ thị (C)
i, Khảo sát hàm số.
ii, Dựa vào đồ thực biện luận số nghiệm của pt: 
HS: i,
* TXĐ: D = R, "x ẻ D => -x ẻ D
f(-x) = f(x) " x ẻ D.
=> hàm số chẵn --> Đồ thị nhận oy làm trục đối xứng.
f(-x) = f(x) "x ẻ D.
* Sự biến thiên:
+) y' = 4x3 - 4x = 4x(x2 -1).
x
-Ơ
-1
0
1
2
+Ơ
y'
_
0
+
-
+
x = 0; yCĐ = y(0) = 0.
y"=12x2 - 4 = 4(3x2 - 1)
HS đồng biến trên khoảng (-1, 0) và (1, +Ơ)
NB trên (-Ơ;1) và (0;1).
+ HS đạt cực trị tại x = -1, x = 1; 
yCT = y(1) = 1
x
-Ơ
+Ơ
y"
+
0
-
0
+
Đồ thị
Lõm
Điểm uốn
Lồi
Điểm uốn
Lõm
+ BBT:
x
-Ơ
-1
0
1
+Ơ
y'
-
0
+
0
-
0
+
y
+Ơ
0
+Ơ
-1
-1
Hoạt động2
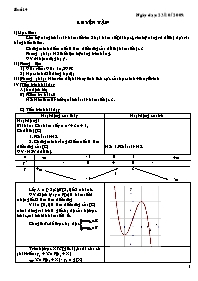
* Đồ thị:
GV: Dựa vào bảng BBT; các điểm cực trị để biết vẽ các trục toạ độ hợp lý các cung lồi, cung lõm, khoảng đồng biến, nghịch biến.
ii, GV: Nguyên tắc viết phương trình cho dưới dạng: f(x) = g(m)
Số nghiệm của phương trình bằng số giao điểm của (C) với đường thẳng y = g(m).
Danh giới phân định: Tung độ các điểm cực trị.
yCT = -1; yCĐ = 0
x4 - 2x2 = 2m - 3
y = f(x) = x4 - 2x2 (C); y = g(m) = 2m - 3 (D)
Dựa vào đồthị: y < -1 Û 2m - 3 < 1 Û m < 1 vô nghiệm.
	Phương trình có 2 nghiệm phân biệt
y = 0 Û 	Phương trình có 3 nghiệm phân biệt
-1 < y < 0 Û 1 < m < 	Phương trình có 4 nghiệm phân biệt
Buổi 5
 Ngày soạn : 30/ 10 / 2009.
 Luyện tập : 
I/ Mục tiêu:
Khảo sát hàm số tổng quát, nghiên cứu tính chất của đồ thị này.
Dựa vào sơ đồ tổng quát để khảo sát.
II/ Phương tiện
Giáo viên: Giáo án, SGK
Học sinh: Đồ dùng học tập
III/ Phương pháp: Nêu vấn đề phát huy tính tích cực của học sinh+thuyết trình
IV/ Tiến trình bài dạy
ổn định lớp
Kiểm tra bài cũ
Tiến trình bài dạy
Hoạt động của thầy
Hoạt động của trò
Hoạt động1
Khảo sát hàm số: với c ạ 0, 
GV,HS: Giải thích
Sự biến thiên:
Không xác định tại x = ẽ D, Không đổi dấu trên D.
- Không có cực trị.
 là TCĐ của đồ thị
=> y = là TCN của đồ thị => Tồn tại tiếp cận xiên.
Đồ thị: Luôn cắt ox, oy 
Đồ thị nhận giao điểm I = ( của 2 tiệm cận là tâm đối xứng
HS: TXĐ: D = R\
 D<0
 D>0
Hoạt động2
VD: 
1, Khảo sát hàm số 
2, Chứng minh rằng I = (1,1) là tâm đối xứng của đồ thị
1, HS
2, GV - HS
x
-Ơ
1
+Ơ
y'
-
||
-
y
1
+Ơ
-Ơ
1
Xét phép đổi hệ trục: 
Khi đó, phương trình của hàm số: Y + 1 = Û Y = "X ẻ D'.
=> Hàm số Y = g(x) lẻ nên nhận gốc I = (0,0) làm tâm đối xứng trên hệ IXY.
Lấy I = 1,1) trên xoy làm tâm đối xứng.
Hoạt động của thầy
Hoạt động của trò
Hoạt động1
GV: cho hàm số h = 
a. Khảo sát hàm số
b. Tìm tất cả tâm đối xứng của đồ thị
c. CMR đồ thị luôn cắt đường thẳng (D): y = 2x + m tại 2 điểm phân biệt M, N
GV:
D = | R | { - 1 - x0} 
HS: I = (x0, y0) là tâm đối xứng của (C) 
=> H/s y = g(x) là hàm số lẻ
Xét phép đối trục 
Ta có Y = 
+ g(-x) = - g(x) 
=> 
với "X ạ- x0 - 1
=> y0 = 
với "X ạ- x0 - 1
=> (1-y0)X2 + (x0+1)[ (x0+1)y0 - x0 - 3] với "X ạ- x0 - 1
=> 
D = R* đối xứng qua 0
c. Số giao điểm bằng số n0 của phương trình hoành độ 
=> 
HS
Bài tập:
Xác định m để đoạn MN ngắn nhất.
Hoạt động của thầy
Hoạt động của trò
Buổi 6
 Ngày soạn : 06/ 11 / 2009.
 Luyện tập 
I/ Mục tiêu:
Hình thành nguyên tắc làm việc bài toán tương giao của đồ thị 2 hàm số đặc biệt là bài tập: biện luận số nghiệm của phương trình
NGhiên cứu bài toán tiếp tuyến cơ bản trên cơ sở những kiến thức phương pháp GV - HS
II/ Phương tiện
Giáo viên: Giáo án, SGK
Học sinh: Đồ dùng học tập
III/ Phương pháp: Nêu vấn đề phát huy tính tích cực của học sinh+thuyết trình
IV/ Tiến trình bài dạy
ổn định lớp
Kiểm tra bài cũ
ĐVĐ: xác định tọa độ giao điểm của 2 đường (P) y = x2 - 2x và (D) y = x + 4
HS
Tiến trình bài dạy
Hoạt động của thầy
Hoạt động của trò
Hoạt động1
GV: Bài toán 1
Cho các hàm số y = f(x có đồ thị (C1)
	 y = g(x) có đồ thị (C2)
? Xác định của các giao điểm của (C1) và (C2)
Giả sử M(x0, y0) là 1 giao điểm
? => quan hệ điểm M với (C1)(C2)
M ẻ (C1) ầ (C2) => 
=> (x0, y0) là nghiệm của phương trình 
=> 
? Tìm tọa độ giao điểm của (C1), (C2) ta làm gì?
? Số giao điểm
GV: x0 là nghiệm của (*) tìm tọa độ y từ (**)
Do đó: Số nghiệm của hệ = số nghiệm của (*) = số giao điểm
GV: Mục đích n/c các bài toán có tham số
HS trả lời
HS trả lời
HS trả lời
Hoạt động2
Biện luận số nghiệm của PT: 
 f(x) = g(x( (*)
TH1: Phương trình (*) có bặc 3, 4 Dựa vào đồ thị để biện luận (ứng dụng khảo sát hàm số)
Viết phương trình f(x) = C(m) , m là tham số
Vẽ đồ thị y = F(x) , y = C(m) là đường A có phương nằm ngang
VD1: Biện luận số giao điểm (C1) y = 
VD2: Biện luận số nghiệm của phương trình: x3 + 3x2 +3m - 2 = 0
HS: x3 + 3x2 = m2 - 3m +2
Vẽ đồ thị hàm số y = x3 + 3x2
Hoạt động của thầy
Hoạt động của trò
Hoạt động3
Cho h/s 
1) K/s vẽ đồ thị ( )
2) Biện luận số m phương trình: x3 - 3x + m = 0
3) Viết phương trình T2, biết T2 // d: yx +y - 1 = 0.
Gv:Mốc phân chia khả năng	: y > 3
 : Phương trình có nghiệm
: Phương trình có 2 nghiệm phân biệt.
: Phương trình (1) có 3 nghiệm phân biệt.
Lưu ý: Đối với câu hỏi này: Vẽ đồ thị hoặc lập BBT rồi biện luận, không cần làm đầy đủ các bước bài khảo sát k/s h/s
*) Hs lên bảng vẽ đồ thị ()
*) H/s nêu cách biện luận dựa vào ()
G: 
Số nghiệm của phương trình(1)bằng....
*) ? Cách cho T2 ở trường hợp nào?
HS: hệ số góc tìm hệ số góc của d :
 y = -9x + 1
=> T2 // d nên có hệ số góc k = -9
PT: 
 Có 2 T2 thoả mãn :
 y - 3 = -9(x+2)
y = -9x + 15y - ( - 1) = -9 (x +2)
y = -9x +17 
D.Củng cố-Kiểm tra-Đánh giá
Bài toán 2: Viết phương tình tiếp tuyến cho y = f(x) có đồ thị â
? Viết phương trình tiếp tuyến tại M = (x0, y0) ẻ (C)
? Viết phương trình tiếp tuyến với đồ thị (C)có hệ số góc k
Chưa có tiếp điểm. Gọi M = (x0, y0) có tiếp điểm
gt => K = f'(x0) giải được x0 => y0 => PTTT y - y0 = k(x -x0)
Cách cho: tiếp tuyến // D hoặc T2 ^D
? Viết phương trình tiếp tuyến qua A = (x1, y1)
Giả sử: M = (x0, y0) là tiếp điểm tại M : y - y0 = f'(x) (x0, x0) 
M ẻ (C) : y0 = f(x)
Tiếp tuyến qua A nên ta có: y1 - y0 = f'(x0) (x1 - x0)
Vậy ta có phương trình ẩn x0 : y1 -f(x0) = f'(x0) (x1 - x0)
Ví dụ: Cho hàm số y = -x3 + 3x2 - 4x +2 (C) , viết phương trình tiếp tuyến với (C)
1. Tiếp tuyến ^ A ; D: 1/4x + 3 - y = 0
2. Tiếp tuyến qua A = (1,0)
HS
GV kiểm tra:
ĐS: 1. Có 2 tiếp tuyến là D1: y = - 4x + 2
	D2 = y = - 4x + 6
2. => (x0 - 1)2 = 0 => x0 = 1 -> y 0 = 0 -> f'(x0) = -1
Có duy nhất tiếp tuyến qua A (1,0): y - 0 => y = -x+1
? Bài toán 1: Số giao điểm phụ thuộc số PT hoành độ giao điểm
? Bài toán 2: Số tiếp tuyến ở TH2, TH3, phụ thuộc yếu tố nào?
số nghiệm của phương trình ẩn x0 (vì 1 tiếp điểm có 1 tiếp tuyến )
CHú ý: VD3, Aẻ (C) nhưng tiếp tuyến qua A : - Tiếp tuyến tại A
	 - Tiếp tuyến đi qua A
Viết phương trình tiếp tuyến với đồ thị y = x3 + 3x2 - 2 qua B = (-3, -2) ẻđồ thị
E. Hướng dẫn học tập ở nhà
Ôn tập lại chương II
Buổi 7
 Ngày soạn : 13/ 11 / 2009.
 Luyện tập 
I/ Mục tiêu:
Củng cố kiến thức khảo sát hàm số, bài toán tiếp tuyến tương giao củng cố kiến thức tam bậc 2, phép chia hết,.....
-> Hs chuẩn bị bài ở nhà.
-> Trên lớp GV - lớp chữa bài tập, hướng dẫn giải một số câu hỏi mới về hàm số => mở rộng nhân quan về hàm số.
II/ Phương tiện
Giáo viên: Giáo án, SGK
Học sinh: Đồ dùng học tập
III/ Phương pháp: Nêu vấn đề phát huy tính tích cực của học sinh+thuyết trình
IV/ Tiến trình bài dạy
ổn định lớp
Kiểm tra bài cũ
Tiến trình bài dạy
Hoạt động của thầy
Hoạt động của trò
Hoạt động1
Bài toán: Cho 
a) m = 1. Khảo sát hàm số
b) X/đ m để h/s i) đồng biến trên
	 ii)	có cực trị (
c> CMR: ( C luôn cắt ox tại 2 điểm p/b M, N. Xác định m để NM nhỏ hơn
ii) 
HS a,
b, 
1, H/s đ/b trên trên ( < đl mở rộng, 
	 trên (3;	
x
 - +
y'
 - 0 +
c) Hs: pt hoành độ giao điểm: 
"m
PT (1) có 2 nghiệm p/b cắt trục 0x tại 2 điểm M, N
Gv: X/đ toạ độ giao điểm N, M => độ dài MN
M = với vì MN ox
 là 2 nghiệm của PT (1).
	m R
Tìm min g(m) 	
g(m) = 	" m
g(m) = 1 m = 1 € R
Vậy min [MN] = 1 
Bài toán 2:
1) Xác định m để h/s có 1 CĐ, KT . Tính toạ độ CT.
y = 
ii) m? h/s đ/b trên TXĐ.
GV i) Xét CĐ, CT dựa vào ý
TH1: 
H/s luôn có 1 cực trị là CT, 
ycbt (2; 
HS: 1N = 
Định luật Viet
Hoặc công thức nghiệm
Hs ii) ycbt 	
"x vì y' = 0 có nhiều nhất 2 nghiệm 
( HS có CĐ, CT có 2 nghiệm p/b vì y' là tam thức bậc 2> y' = 0 
Đk: m
x
- +
y
+ 0 - 0 +
Xcđ = x1, Xct = x2 = 2m - 1 => yct = 
TH2: x1>x2 m<1
x
- +
y
+ 0 - 0 +
	=> xCĐ = x2, xCT = x1 = 1, Yct = 
KL: m1, h/s có 1 CĐ, 1 CT 
Nếu m>1: XCT = , YCT = 
Nếu m<1 ; XCT = ; YCT = 
Hoạt động3
GV? Nêu kết quả k/s hàm số bậc 3
Bài toán 3: Cho h/s 
1. Biện luận số nghiệm của phương trình: 
2. Viết phương trình t2 tại điểm uốn, cực trị của ( 
3. Viết phương trình T2 với ( Qua gốc toạ độ
4. CMR: đồ thị ( có tâm đối xứng.
 GV: Cách làm bài toán này.
HS: trả lời
H.s: 
Vẽ đồ thị (): . Vẽ đường thẳng y = 5 - 3m
Biện luận:
GV: Kiểm tra kết quả
2> Các điểm uốn cực trị có đặc điểm gì, loại bài toán tiếp tuyến nào?
3?. Loại bài toán T2	
H.S. với 
Vì T2 qua O = (0; 0) nên : 0- y0 = f'(x0)( 0 - x0)
Vậy ta có 2 T2 qua o
4. ? Hiểu câu hỏi như thế nào?
-> C1: Chỉ ra 1 điểm là tâm đx.
-> C2: Trừ tâm đối xứng
C1: đơn giản hơn hàm sốm bậc 3 nhận điểm uốn là tâm đối xứng
GV: Chữa bài SGK
Xét phương trình: ( trùng phương)
Chung về bậc 2: t = x2, đk: t
có 2 nghiệm dương t1t2, t1 < t2 
=>(1) có 4 nghiệm dương: 
Lập thành 
ycbt ( 1' ) có hai nghiệm và ( p/b rồi)
2) GV - Hs chữa bài tập, gợi ý
GV: Dạng phân thức - tối giản biểu thức.
? Những điểm có toạ độ nguyên dương.
Vẫn làm như trên loại bỏ những toạ độ không thoả mãn yêu cầu.
*) 9d - sgk: P2 bỏ dấu định nghĩa hoặc bình phương.
Gv: Với câu hỏi dài ta làm từng y/c
S = (x0;y0) với y0 = 
PT T2 tại S:
Các tiệm cận của là: x = -1; y = 1
P = TCĐ = 
Q = TCN = 
CM: S là trung điểm PQ ( vì P, Q, S 
*) 11- SGK.
c) T/c của tâm đx I = ( - 1; -1)
ĐI: thì 
ĐI: M là tiếp điểm => N là tiếp điểm.
Nguyên tắc: M( N đx M qua I.
c/m t2 tại M, N song song.
d) 0A^0B 
*)12 d - sgk: M, N, P, Q 
ycbt 
*) 13b) Nếu có tiệm cận xiên
Y = 
Thì TCX: y = Đi qua O(0, 0) Thử lại 
H/s phân thức
*) 9b - SGK: Từ M = (x0; y0) 
Củng cố-Kiểm tra-Đánh giá
Chia các bài toán trên, các yc đối với bài toán hàm số rất đa dạng có những câu hỏi phải vận dụng kiến thức tổng hợp: ĐS - GT - HH 
Nguyên Tắc: Thực hiện dần các yêu cầu theo đề bài chỉ dẫn -> bài toán đã biết 
Hướng dẫn học tập ở nhà
Nắm vững kiến thức đã học của chương