Giáo án Giải tích 12 - Tiết 7 - Bài 3: Giá trị lớn nhất, giá trị nhỏ nhất

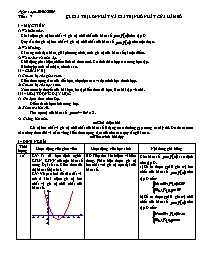
Ngày soạn:20/08/2009	
Tiết : 	7	§3. GIÁ TRỊ LỚN NHẤT VÀ GIÁ TRỊ NHỎ NHẤT CỦA HÀM SỐ 
I – MỤC TIÊU
1) Về kiến thức: 
 Khái niệm giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên tập D
 Quy tắc tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên một đoạn.
2) Về kĩ năng:
 Kĩ năng tính đạo hàm, giải phương trình, tính giá trị của hàm số tại một điểm.
3) Về tư duy và thái độ:
 Chủ động phát hiện, chiếm lĩnh tri thức mới. Có tinh thần hợp tác trong học tập.
 Rèn luyện tính cẩn thận, chính xác.
II – CHUẨN BỊ 
1) Chuẩn bị của giáo viên:
 Kiến thức trọng tâm của tiết học, chọn lọc các ví dụ minh họa thích hợp.
2) Chuẩn bị của học sinh:
 Xem trước lý thuyết của bài học, ôn tập kiến thức đã học, làm bài tập về nhà.
III – HOẠT ĐỘNG DẠY HỌC
1) Ổn định tình hình lớp:
	Điểm danh học sinh trong lớp.	
2) Kiểm tra bài cũ:	
	Tìm cực trị của hàm số .
3) Giảng bài mới:
@ Giới thiệu bài
	Giá trị lớn nhất và giá trị nhỏ nhất của hàm số là dạng toán thường gặp trong các kỳ thi. Do đó các em cần chú ý theo dõi và nắm vững kiến thức trọng tâm của như các quy tắc giải toán.
@ Tiến trình bài dạy
I – ĐỊNH NGHĨA
Thời lượng
Hoạt động của giáo viên 
Hoạt động của học sinh
Nội dung ghi bảng
10’
GV: Ta đã học định nghĩa GTLN, GTNN của một hàm số trong Đại số 10. Kiến thức đồ thị hàm số bậc hai. 
GV: Vẽ parabol để dẫn dắt và mô tả khái niệm giá trị lớn nhất và giá trị nhỏ nhất của hàm số.
HS: Tiếp thu khái niệm và hiểu đúng. Phân biệt được giá trị lớn nhất với giá trị cực đại của hàm số.
Cho hàm số xác định trên tập D.
a) Số M được gọi là giá trị lớn nhất của hàm số trên tập D nếu:
b) Số m được gọi là giá trị nhỏ nhất của hàm số trên tập D nếu:
II- CÁCH TÍNH GIÁ TRỊ LỚN NHẤT VÀ GIÁ TRỊ NHỎ NHẤT CỦA HÀM SỐ TRÊN MỘT ĐOẠN
1. Định lí
Thời lượng
Hoạt động của giáo viên 
Hoạt động của học sinh
Nội dung ghi bảng
3’
GV: Với định lí này, khi gặp bài toán tìm GTLN, GTNN của hàm số trên một đoạn là luôn tồn tại.
HS: Nhớ và hiểu đúng ý nghĩa của nội dung định lí này.
Mọi hàm số liên tục trên một đoạn đều có giá trị lớn nhất và giá trị nhỏ nhất trên đoạn đó.
2. Quy tắc tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số liên tục trên một đoạn
Thời lượng
Hoạt động của giáo viên 
Hoạt động của học sinh
Nội dung ghi bảng
28’
GV: Khi gặp dạng toán tìm GTLN, GTNN trên một đoạn thì ta áp dụng quy tắc.
GV: Đưa ra các ví dụ sau để áp dụng quy tắc.
Tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số:
1) 
 trên đoạn .
2) 
 trên đoạn .
3) 
 trên đoạn .
4) trên đoạn .
HS: Hiểu đúng và vận dụng được quy tắc tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn .
HS: Biết tính đạo hàm và giải phương trình .
QUY TẮC
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn .
1. Tìm các điểm trên khoảng , tại đó bằng 0 hoặc không xác định.
2. Tính: .
3. Tìm số lớn nhất M và số nhỏ nhất m trong các số trên. Ta có 
 , 
4) Dặn dò học sinh chuẩn bị cho tiết học tiếp theo:
- Ra bài tập về nhà: 
	Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số:
1) trên đoạn .
2) trên đoạn 
- Chuẩn bị bài: 
	Xem tiếp nội dung bài học, học bài cũ và giải bài tập về nhà.
IV – RÚT KINH NGHIỆM, BỔ SUNG
Ngày soạn:20/08/2009	
Tiết : 	8	§3. GIÁ TRỊ LỚN NHẤT VÀ GIÁ TRỊ NHỎ NHẤT CỦA HÀM SỐ 
I – MỤC TIÊU
1) Về kiến thức: 
 Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên một khoảng.
2) Về kĩ năng:
 Kĩ năng tính đạo hàm, lập bảng biến thiên, xét dấu y’.
3) Về tư duy và thái độ:
 Chủ động phát hiện, chiếm lĩnh tri thức mới. Có tinh thần hợp tác trong học tập.
 Rèn luyện tính cẩn thận, chính xác.
II – CHUẨN BỊ 
1) Chuẩn bị của giáo viên:
 Phương pháp tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên một khoảng. Các ví dụ minh họa.
2) Chuẩn bị của học sinh:
 HỌc bài cũ, làm bài tập về nhà, xem trước nội dung bài mới.
III – HOẠT ĐỘNG DẠY HỌC
1) Ổn định tình hình lớp:
	Điểm danh học sinh trong lớp.	
2) Kiểm tra bài cũ:	
	Tìm GTLN, GTNN của hàm số trên đoạn 
3) Giảng bài mới:
@ Giới thiệu bài
 Hàm số liên tục trên một khoảng có thể không có giá trị lớn nhất và giá trị nhỏ nhất trên khoảng đó. Chẳng hạn hàm số . Tuy nhiên có những hàm số có giá trị lớn nhất hoặc giá trị nhỏ nhất trên một khoảng.
@ Tiến trình bài dạy
3. Quy tắc tìm giá trị lớn nhất và giá trị nhỏ nhất trên một khoảng
Thời lượng
Hoạt động của giáo viên 
Hoạt động của học sinh
Nội dung ghi bảng
10’
GV: Khi gặp dạng toán giá trị lớn nhất và giá trị nhỏ nhất trên một khoảng thì ta dùng quy tắc trên khoảng không được dùng quy tắc trên đoạn.
HS: Nắm vững và vận dụng hai quy tắc giá trị lớn nhất và giá trị nhỏ nhất trên một đoạn và trên một khoảng.
Quy tắc tìm giá trị lớn nhất và giá trị nhỏ nhất trên một khoảng
1. Tìm tập xác định.
2. Lập bảng biến thiên.
GV: Khi gặp bài toán giá trị lớn nhất và giá trị nhỏ nhất không nói rõ ở đâu. Ta tự hiểu là tìm trên tập xác định của nó.
HS: Biết được cách dùng trong các khả năng khác nhau của bài toán giá trị lớn nhất và giá trị nhỏ nhất.
3. Kết luận.
15’
Ví dụ 1. Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số:
trên khoảng .
Ví dụ 2. Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số:
trên khoảng .
Thời lượng
Hoạt động của giáo viên 
Hoạt động của học sinh
Nội dung ghi bảng
18’
Ví dụ 3. 
 Cho một tấm nhôm hình vuông cạnh a. người ta cắt ở bốn góc bốn hình vuông bằng nhau, rồi gập tấm nhôm lại (như hình vẽ) để được một cái hộp không nắp. Tính cạnh của các hình vuông bị cắt sao cho thể tích của khối hộp lớn nhất.
GV: Tính đạo hàm của hàm số V(x) và giải phương trình . Tìm các nghiệm là 
GV: Lập bảng biến thiên. Từ đó kết luận.
HS: Vẽ hình
HS: Nhận biết được đây là dạng toán ứng dụng thực tế. Học sinh ghi nhớ và có thể vận dụng trong cuộc sống.
Trình bày bài giải trong sách giáo khoa.
Gọi x là độ dài của cạnh hình vuông bị cắt.
Điều kiện 
Các cạnh của hình hộp lần lượt là: .
Thể tích của khối hộp là:
Ta cần tìm giá trị lớn nhất của hàm số trên khoảng .
4) Dặn dò học sinh chuẩn bị cho tiết học tiếp theo:
- Ra bài tập về nhà: 
	Giải các bài tập 1, 2, 4, 5 SGK – Trang 24.
- Chuẩn bị bài: 
	Học bài cũ, giải bài tập về nhà.
IV – RÚT KINH NGHIỆM, BỔ SUNG
Ngày soạn:20/08/2009	BÀI TẬP	
Tiết : 	9	§3. GIÁ TRỊ LỚN NHẤT VÀ GIÁ TRỊ NHỎ NHẤT CỦA HÀM SỐ 
I – MỤC TIÊU
1) Về kiến thức: 
 Quy tắc tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số.
2) Về kĩ năng:
 Kĩ năng tính đạo hàm, giải phương trình, tính giá trị của hàm số tại một điểm.
3) Về tư duy và thái độ:
 Chủ động phát hiện, chiếm lĩnh tri thức mới. Có tinh thần hợp tác trong học tập.
 Rèn luyện tính cẩn thận, chính xác.
II – CHUẨN BỊ 
1) Chuẩn bị của giáo viên:
 Chuẩn bị một số bài tập ôn tập nhằm củng cố và khắc sâu khái niệm và quy tắc cho học sinh.
2) Chuẩn bị của học sinh:
 Học bài cũ, giải bài tập về nhà.
III – HOẠT ĐỘNG DẠY HỌC
1) Ổn định tình hình lớp:
 Điểm danh học sinh trong lớp.	
2) Kiểm tra bài cũ:	
	Tìm GTLN, GTNN của hàm số trên đoạn .
3) Giảng bài mới:
@ Giới thiệu bài
	Giải bài tập nhiều giúp chúng và phản xạ nhanh các dạng toán, đồng thời rèn luyện kĩ năng tính toán.
@ Tiến trình bài dạy
Bài 1. Tìm GTLN, GTNN của hàm số: 
a) 	b) 
c) 	d) trên đoạn 
Thời lượng
Hoạt động của giáo viên 
Hoạt động của học sinh
Nội dung ghi bảng
18’
-Chia hs thành 4 nhóm, mỗi nhóm làm 1 câu rồi cử đại diện trình bày LG.
-GV cùng hs chính xác hoá lời giải.
-GV lưu ý học sinh :
 +lựa chọn PP phù hợp.
 + ĐK thứ hai của định nghĩa.
 +Khi đổi biến phải lưu ý điều kiện của biến số mới và tập khảo sát mới.
-Thảo luận nhóm tìm lời giải bài tâp1.
-Mối nhóm cử đại diện trình bày LG.
-Các thành viên của nhóm khác chú ý nghe để phản biện và nhận xét, bổ sung cách giải khác.
Bài tập 1: 
a/ TXĐ: R
y=1-sin22x y1
miny= khi x=;
maxy =1 khi x = .
b/ đặt t=sin2x, -1t1
c/ Đặt t=x2 , ĐK: 0t1
d/ đặt t=sinx, ĐK: 0t1
Bài 2. Khi nuôi cá thí nghiệm trong hồ, một nhà sinh vật học thấy rằng: Nếu trên mỗi đơn vị diện tích của mặt hồ có n con cá thì trung bình mỗi con cá sau một vụ cân nặng:
P(n)= 480-20n (gam). Hỏi phải thả bao nhiêu cá trên một đơn vị diện tích của mặt hồ để sau một vụ thu hoạch được nhiều cá nhất.
Thời lượng
Hoạt động của giáo viên 
Hoạt động của học sinh
Nội dung ghi bảng
10’
-Phát vấn, gợi mở, vấn đáp học sinh.
- Nếu trên mỗi đơn vị diện tích của mặt hồ có n con cá thì sau một vụ số cá trên mỗi đơn vị diện tích mặt hồ trung bình cân nặng là bn?
-Cho HS khảo sát hs: f(x)=480x-20x2 trên hkoảng (0;+). (biến thực).
-Từ BBT suy ra kq với biến thực x, suy ra với n.
-Suy nghĩ trả lời câu hỏi của giáo viên để xây dựng lời giải.
+ f(n)=n.P(n)=480n-20n2 (g).
-Khảo sát hs: f(x)=480x-20x2 trên hkoảng (0;+). (biến thực).
-Kết luận.
Lời giải: Nếu trên mỗi đơn vị diện tích của mặt hồ có n con cá thì sau một vụ số cá trên mỗi đơn vị diện tích mặt hồ trung bình cân nặng:
f(n)=n.P(n)=480n-20n2 (g).
Xét hs f(x)=480x-20x2 trên hkoảng (0;+). (biến thực)
-Từ BBT có: =f(12)
trên N* f đạt GTLN khi n=12. Vậy thả 12 con cá.
Bài 3. Trong các hình chữ nhật nội tiếp đường tròn (O;R). Tìm hình chữ nhật có diện tích lớn nhất.
Thời lượng
Hoạt động của giáo viên 
Hoạt động của học sinh
Nội dung ghi bảng
8’
-Cho học sinh độc lập suy nghĩ tìm lời giải, gọi một học sinh trình bày lời giải, lớp nhận xét, bổ sung.
- GV uốn nắn sự biểu đạt của học sinh về tính toán, cách trình bày bài giải.
-Nêu cách giải khác? (áp dụng BĐT ).
-Độc lập lập suy nghĩ tìm lời giải.
-Trình bày lời giải.
-Nhận xét, bổ sung, sửa chữa bài của bạn.
-Nêu cách giải khác.
-Ghi nhận kiến thức.
- Lời giải BT3. 
4) Dặn dò học sinh chuẩn bị cho tiết học tiếp theo:
- Ra bài tập về nhà: 
	Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số 
- Chuẩn bị bài: 
	Xem trước nội dung bài học tiếp theo. §4. Đường tiệm cận.
IV – RÚT KINH NGHIỆM, BỔ SUNG