Giáo án Giải tích 12 NC - Tiết 19: Ôn tập chương I

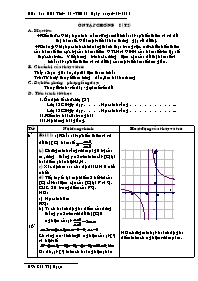
Ôn tập chương I (T2)
A. Mục tiêu
+Kiến thức : Giúp học sinh nắm vững sơ đồ khảo sát sự biến thiên và vẽ đồ thị hàm số. Giải một số bài toán thường gặp về đồ thị.
+Kĩ năng: Giúp học sinh có kĩ năng thành thạo trong việc xét chiều biến thiên của hàm số tìm cực trị của hàm số tìm GTLN và GINN của hàm số trên tập số thực cho trước. Viết phương trình các đường tiệm cận của đồ thị hàm số và khảo sát sự biến thiên và vẽ đồ thị của một số hàm số đơn giản.
B. Chuẩn bị của thày và trò:
Thầy : Soạn giáo án, đọc tài liệu tham khảo
Trò: Từ ôn lý thuyết theo hướng dẫn, làm bài ôn chương
C. Dự kiến phương pháp giảng dạy: 
 Thuyết trình-vấn đáp - gợi mở vấn đề
D. Tiến trình tiết học 
I. ổn định tổ chức lớp (2’)
Lớp12C1Ngày dạyHọc sinh vắng..
Lớp12C2Ngày dạyHọc sinh vắng..
 II.Kiểm tra bài cũ: trong bài
 III. Nội dung bài giảng.
TG
Nội dung chính
Hoạt động của thày và trò
8’
10’
10’
10’
5’
Bài 11: a) Khảo sát sự biến thiên và vẽ đồ thị ( C) hàm số .
b) Chứng minh rằng với mọi giá trị của m , đường thẳng y=2x+m luôn cắt (C) tại hai điểm phân biệt M,N .
c) Xác định m sao cho độ dài MN là nhỏ nhất.
d) Tiếp tuyến tại một điểm S bất kì của (C) cắt hai tiệm cận của (C) tại P và Q . CMR S là trung điểm của PQ.
HD: 
Học sinh làm 
KQ:
Ta có hoành độ giao điểm của đường thẳng y=2x+m với đồ thị (C) là nghiệm của pt 
Rõ ràng x=-1 không là nghiệm của pt (*) và biệt số 
Do đó , pt (*) luôn có hai nghiệm phân biệt khác -1.
Vậy đường thẳng y=2x+m luôn cắt (C) tại hai điểm phân biệt M và N.
Ta có các hoành độ xm, xn lần lượt của các điểm M,N là hai nghiệm phân biệt của pt (*) nên theo định lý viets:
độ dài MN nhỏ nhất khi và chỉ khi MN2 nhỏ nhất.
Ta có 
Hay 
Dấu bằng xảy ra khi và chỉ khi m-3=0 hay m=3.
Khi đó độ dài nhỏ nhất của MN là .
Giả sử S(x0,y0) là điểm bất kì thuộc (C). ta có phương trình tiếp tuyến (T) của (C) tại S là :
 trong đó 
Giao điểm (T) với tiệm cận ngang là điểm P( 2x0+1;1). Giao điểm của (T) với tiệm cận đứng là điểm 
Rõ ràng nên S là trung điểm của PQ.
Bài 12: GV hd học sinh làm
IV. Củng cố 
V. Hướng dẫn về nhà: Bài tập về nhà: các bài tập còn lại
Chuẩn bị kiểm tra 1 tiết
HD: chứng minh pt hoành độ giao điểm luôn có nghiệm với mọi m.
Hãy tính độ dài MN theo m-dựa vào định lý viét
Lập pttt (T) tại điểm S(x0,y0) thuộc (C)
Tìm giao điểm của (T) với các tiệm cận ;từ đó cm S là trung điểm của các giao điểm đó.
KQ: bài 12: 
Cả hai gt trên đều nằm ngoài đoạn [-1;1].nên pt đã cho vô nghiệm.
b) kq: .
c)KQ:
Nhận xét và chữ kí của tổ trưởng: