Giáo án Giải tích 12 cả năm chuẩn kiến thức

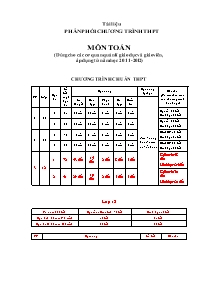
Tài liệu
PHÂN PHỐI CHƯƠNG TRÌNH THPT
MÔN TOÁN
(Dùng cho các cơ quan quản lí giáo dục và giáo viên,
áp dụng từ năm học 2011-2012)
CHƯƠNG TRÌNH CHUẨN THPT 
TT
Lớp
Học
kì
Số tiết
một học
kì
Nội dung
Nội dung
tự chọn
Ghi chú
(Số tiết theo môn của chương trình bắt buộc)
Lí thuyết
Bài tập
Thực
hành
Ôn
tập
Kiểm tra
Xem hướng dẫn chi tiết
ở phần dưới
1
10
1
54
31 tiết
11 tiết
2 tiết
5 tiết
5 tiết
Đạí số: 32 tiết
Hìnhhọc:22tiết
2
51
29 tiết
10 tiết
2 tiết
5 tiết
5 tiết
Đạí số: 30 tiết
Hìnhhọc:21tiết
2
11
1
72
43 tiết
14 tiết
2 tiết
8 tiết
5 tiết
ĐS>:48 tiết
Hìnhhọc:24tiết
2
51
29 tiết
10 tiết
2 tiết
5 tiết
5 tiết
ĐS>:30 tiết
Hìnhhọc:21tiết
3
12
1
72
43 tiết
14 tiết
2 tiết
8 tiết
5 tiết
Gíảítích:48 tiết
Hìnhhọc:24tiết
2
51
29 tiết
10 tiết
2 tiết
5 tiết
5 tiết
Gíảítích:30 tiết
Hìnhhọc:21tiết
Lớp 12
Cả năm 123 tiết
Đại số và Giải tích 78 tiết
Hình học 45 tiết
Học kì I: 19 tuần (72 tiết)
48 tiết
24 tiết 
Học kì II: 18 tuần (51 tiết)
30 tiết
21 tiết
TT
Nội dung
Số tiết
Ghi chú
1
ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số
Sự đồng biến, nghịch biến của hàm số . Cực trị của hàm số. Giá trị lớn nhất và giá trị nhỏ nhất của hàm số. Đường tiệm cận đứng, đường tiệm cận ngang của đồ thị hàm số. Khảo sát sự biến thiên và vẽ đồ thị của hàm số
20
Đại số 78 tiết
(trong đó có tiết ôn tập, kiểm tra, trả bài và tổng ôn thi tốt nghiệp)
2
Hàm số luỹ thừa, hàm số mũ và hàm số lôgarit
Luỹ thừa. Hàm số luỹ thừa. Lôgarit. Hàm số mũ. Hàm số lôgarit. Phương trình mũ và phương trình lôgarit. Bất phương trình mũ và lôgarit
17
3
Nguyên hàm, Tích phân và ứng dụng
Nguyên hàm. Tích phân. ứng dụng của tích phân trong hình học. 
16
4
Số phức
Số phức. Cộng, trừ và nhân số phức. Phép chia số phức. Phương trình bậc hai với hệ số thực
9
5
Khối đa diện
Khái niệm về khối đa diện. Khối đa diện lồi và khối đa diện đều. Khái niệm về thể tích của khối đa diện
11
Hình học 45 tiết
(trong đó có tiết ôn tập, kiểm tra, trả bài và tổng ôn thi tốt nghiệp)
6
Mặt nón, mặt trụ, mặt cầu
Khái niệm về mặt tròn xoay. Mặt cầu
10
7
Phương pháp toạ độ trong không gian
Hệ toạ độ trong không gian. Phương trình mặt phẳng. Phương trình đường thẳng trong không gian.
18
Tiết: 1 Ngµy so¹n ......................
Bµi 1: Sù ®ång biÕn, nghÞch biÕn cña hµm sè 
I. MỤC TIÊU:
1/ Kiến thức: 	
+ Củng cố khái niệm hàm số đồng biến, nghịch biến
+ Nắm được mối liên hệ giữa dấu của đạo hàm và tính đơn điệu của hàm số.
	+ Nắm được qui tắc xét tính đơn điệu của hàm số.
2/ Kỹ năng: Biết xét tính đơn điệu của một số hàm số đơn giản. 
Biết kết hợp nhiều kiến thức liên quan để giải toán.
3/ Tư duy và thái độ: Thận trọng, chính xác.
II. CHUẨN BỊ.
	+ GV: Giáo án, bảng phụ.
	+ HS: SGK, đọc trước bài học.
III. PHƯƠNG PHÁP.
	Thông qua các hoạt động tương tác giữa trò – trò, thầy – trò để lĩnh hội kiến thức, kĩ năng theo mục tiêu bài học. 
 Phèi hîp c¸c ph­¬ng ph¸p thuyÕt tr×nh,vÊn ®¸p gîi më minh ho¹
 §an xen c¸c d¹ng ho¹t ®éng cña häc sinh 
IV. TIẾN TRÌNH DẠY HỌC.
* Ổn định và làm quen, giới thiệu tổng quan chương trình Giải tích 12 chuẩn (5')
* Bài mới:
Tg
HĐ của GV
HĐ của HS
Ghi bảng
10'
Hoạt động 1: Nhắc lại các kiến thức liên quan tới tính đơn điệu của hàm số
Gv treo bảng phụ có hình vẽ H1 và H2 - SGK trg 4.
Phát vấn:
+ Các em hãy chỉ ra các khoảng tăng, giảm của các hàm số, trên các đoạn đã cho?
+ Nhắc lại định nghĩa tính đơn điệu của hàm số?
+ Nhắc lại phương pháp xét tính đơn điệu của hàm số đã học ở lớp dưới?
+ Nêu lên mối liên hệ giữa đồ thị của hàm số và tính đơn điệu của hàm số?
+ Ôn tập lại kiến thức cũ thông qua việc trả lời các câu hỏi phát vấn của giáo viên.
+ Ghi nhớ kiến thức.
I. Tính đơn điệu của hàm số:
1. Nhắc lại định nghĩa tính đơn điệu của hàm số. (SGK)
y
+ Đồ thị của hàm số đồng biến trên K là một đường đi lên từ trái sang phải.
x
O
+ Đồ thị của hàm số nghịch biến trên K là một đường đi xuống từ trái sang phải.
O
x
y
20'
Hoạt động 2: Tìm hiểu mối liên hệ giữa tính đơn điệu của hàm số và dấu của đạo hàm
+ Ra đề bài tập: (Bảng phụ)
Cho các hàm số sau: 
y = 2x - 1 và y = x2 - 2x.
+ Xét dấu đạo hàm của mỗi hàm số và điền vào bảng tương ứng.
+ Phân lớp thành hai nhóm, mỗi nhóm giải một câu.
+ Gọi hai đại diện lên trình bày lời giải lên bảng
+ Có nhận xét gì về mối liên hệ giữa tính đơn điệu và dấu của đạo hàm của hai hàm số trên?
+ Rút ra nhận xét chung và cho HS lĩnh hội ĐL 1 trang 6.
+ Giải bài tập theo yêu cầu của giáo viên.
+ Hai học sinh đại diện lên bảng trình bày lời giải.
+ Rút ra mối liên hệ giữa tính đơn điệu của hàm số và dấu của đạo hàm của hàm số.
I. Tính đơn điệu của hàm số:
2. Tính đơn điệu và dấu của đạo hàm: 
* Định lí 1: (SGK)
Cho hàm số y = f(x) có đạo hàm trên K
* Nếu f'(x) > 0 thì hàm số y = f(x) đồng biến trên K.
* Nếu f'(x) < 0 thì hàm số y = f(x) nghịch biến trên K.
10'
Hoạt động 3: Giải bài tập củng cố định lí.
+ Giáo viên ra bài tập 1.
+ GV hướng dẫn học sinh lập BBT.
+ Gọi 1 hs lên trình bày lời giải.
+ Điều chỉnh lời giải cho hoàn chỉnh.
+ Các Hs làm bài tập được giao theo hướng dẫn của giáo viên.
+ Một hs lên bảng trình bày lời giải.
+ Ghi nhận lời giải hoàn chỉnh. 
Bài tập 1: Tìm các khoảng đồng biến, nghịch biến của hàm số: y = x3 - 3x + 1.
Giải:
+ TXĐ: D = R.
+ y' = 3x2 - 3.
 y' = 0 Û x = 1 hoặc x = -1.
+ BBT:
x - ¥ -1 1 + ¥
y' + 0 - 0 +
y
+ Kết luận:
gi¸o ¸n ®¹i sè – h×nh häc 12 c¬ b¶n c¶ n¨m chuÈn kiÕn thøc kü n¨ng míi 2011-2012
liªn hÖ ®t 01689218668
Tiết: 2 
Bµi 1: Sù ®ång biÕn, nghÞch biÕn cña hµm sè 
I. MỤC TIÊU:
1/ Kiến thức: 	
	+ Nắm được qui tắc xét tính đơn điệu của hàm số.
2/ Kỹ năng: Biết xét tính đơn điệu của một số hàm số đơn giản. 
Biết kết hợp nhiều kiến thức liên quan để giải toán.
3/ Tư duy và thái độ: Thận trọng, chính xác.
II. CHUẨN BỊ.
	+ GV: Giáo án, bảng phụ.
	+ HS: SGK, đọc trước bài học.
III. PHƯƠNG PHÁP.
	Thông qua các hoạt động tương tác giữa trò – trò, thầy – trò để lĩnh hội kiến thức, kĩ năng theo mục tiêu bài học. 
 Phèi hîp c¸c ph­¬ng ph¸p thuyÕt tr×nh,vÊn ®¸p gîi më minh ho¹
 §an xen c¸c d¹ng ho¹t ®éng cña häc sinh 
IV. TIẾN TRÌNH DẠY HỌC.
10'
Hoạt động 1: Mở rộng định lí về mối liên hệ giữa dấu của đạo hàm và tính đơn điệu của hàm số
+ GV nêu định lí mở rộng và chú ý cho hs là dấu "=" xảy ra tại một số hữu hạn điểm thuộc K.
+ Ra ví dụ.
+ Phát vấn kết quả và giải thích.
+ Ghi nhận kiến thức.
+ Giải ví dụ.
+ Trình bày kết quả và giải thích.
I. Tính đơn điệu của hàm số:
2. Tính đơn điệu và dấu của đạo hàm: 
* Định lí: (SGK)
* Chú ý: (SGK)
+ Ví dụ: Xét tính đơn điệu của hàm số y = x3.
ĐS: Hàm số luôn đồng biến.
7'
Hoạt động 2: Tiếp cận quy tắc xét tính đơn điệu của hàm số
+ Từ các ví dụ trên, hãy rút ra quy tắc xét tính đơn điệu của hàm số?
+ Nhấn mạnh các điểm cần lưu ý.
+ Tham khảo SGK để rút ra quy tắc.
+ Ghi nhận kiến thức
II. Quy tắc xét tính đơn điệu của hàm số.
1. Quy tắc: (SGK)
+ Lưu ý: Việc tìm các khoảng đồng biến, nghịch biến của hàm số còn được gọi là xét chiều biến thiên của hàm số đó.
13'
Hoạt động 3: Áp dụng quy tắc để giải một số bài tập liên quan đến tính đơn điệu của hàm số
+ Ra đề bài tập.
+ Quan sát và hướng dẫn (nếu cần) học sinh giải bài tập.
+ Gọi học sinh trình bày lời giải lên bảng.
+ Hoàn chỉnh lời giải cho học sinh.
+ Giải bài tập theo hướng dẫn của giáo viên.
+ Trình bày lời giải lên bảng.
+ Ghi nhận lời giải hoàn chỉnh.
Bài tập 2: Xét tính đơn điệu của hàm số sau:
ĐS: Hàm số đồng biến trên các khoảng và 
Bài tập 3:
Chứng minh rằng: tanx > x với mọi x thuộc khoảng 
HD: Xét tính đơn điệu của hàm số y = tanx - x trên khoảng . từ đó rút ra bđt cần chứng minh.
5'
Hoạt động 4: Tổng kết
+ Gv tổng kết lại các vấn đề trọng tâm của bài học
Ghi nhận kiến thức
* Qua bài học học sinh cần nắm được các vấn đề sau:
+ Mối liên hệ giữa đạo hàm và tính đơn điệu của hàm số.
+ Quy tắc xét tính đơn điệu của hàm số.
+ Ứng dụng để chứng minh BĐT.
Củng cố:
Cho hàm số f(x) = và các mệnh đề sau:
(I) : Trên khoảng (2; 3) hàm số f đồng biến.
(II): Trên các khoảng (- ; 1) và (1; +) đồ thị của hàm số f đi lên từ trái qua phải.
(III): f(x) > f(2) với mọi x thuộc khoảng (2; + ).
Trong các mệnh đề trên có bao nhiêu mệnh đề đúng?
A. 1	B. 3	C. 2	D. 0
	HS trả lời đáp án.
	GV nhận xét.
* Hướng dẫn học bài ở nhà và ra bài tập về nhà:
	+ Nắm vững qui tắc xét tính đơn điệu của hàm số và ứng dụng.
	+ Giải các bài tập ở sách giáo khoa.
V. PHỤ LỤC:
	Bảng phụ có các hình vẽ H1 và H4 - SGK trang 4
 ********************************************
gi¸o ¸n ®¹i sè – h×nh häc 12 c¬ b¶n c¶ n¨m chuÈn kiÕn thøc kü n¨ng míi 2011-2012
liªn hÖ ®t 01689218668
Tiết: 3 ngµy so¹n ......................
Bµi 2: Cùc trÞ cña hµm sè (Tiết 1/2)
I. Mục tiêu:
1 Về kiến thức:
	+ Biết các khái niệm cực đại, cực tiểu; biết phân biệt các khấi niệm lớn nhất, nhỏ nhất.
	+ Biết các điều kiện đủ để hàm số có cực trị.
2 Về kĩ năng:
	+ Sử dụng thành thạo các điều kiện đủ để tìm cực trị của hàm số.
3 Về tư duy và thái độ:
	+ Hiểu mối quan hệ giữa sự tồn tại cực trị và dấu của đạo hàm.
	+ Cẩn thận, chính xác; Tích cực hoạt động; rèn luyện tư duy trực quan, tương tự.
II. Chuẩn bị:
* Giáo viên: Giáo án, bảng phụ
* Học sinh: Nắm kiến thức bài cũ, nghiên cứu bài mới, đồ dùng học tập.
III. Phương pháp: 
	Kết hợp nhiều phương pháp, trong đó vấn đáp, gợi mở là phương pháp chủ đạo.
 §an xen c¸c d¹ng ho¹t ®éng cña häc sinh
IV. Tiến trình: 
1. Ổn định tổ chức (1’): Kiểm tra tác phong, sỉ số, thái độ học tập
2. Kiểm tra bài cũ (5’): Xét sự đồng biến, nghịch bến của hàm số: 
3. Bài mới (tiết số 1)
Hoạt động 1: Khái niệm cực trị và điều kiện đủ để hàm số có cực trị.
TG
HĐGV
HĐHS
GB
+ Treo bảng phụ (H8 tr 13 SGK) và giới thiệu đây là đồ thị của hàm số trên.
H1 Dựa vào đồ thị, hãy chỉ ra các điểm tại đó hàm số có giá trị lớn nhất trên khoảng ? 
H2 Dựa vào đồ thị, hãy chỉ ra các điểm tại đó hàm số có giá trị nhỏ nhất trên khoảng ? 
+ Cho HS khác nhận xét sau đó GV chính xác hoá câu trả lời và giới thiệu điểm đó là cực đại (cực tiểu).
+ Cho học sinh phát biểu nội dung định nghĩa ở SGK, đồng thời GV giới thiệu chú ý 1. và 2.
+ Từ H8, GV kẻ tiếp tuyến tại các điểm cực trị và dẫn dắt đến chú ý 3. và nhấn mạnh: nếu thì không phải là điểm cực trị.
+ Yêu cầu HS xem lại đồ thị ở bảng phụ và bảng biến thiên ở phần KTBC (Khi đã được chính xác hoá).
H1 Nêu mối liên hệ giữa tồn tại cực trị và dấu của đạo hàm?
+ Cho HS nhận xét và GV chính xác hoá kiến thức, từ đó dẫn dắt đến nội dung định lí 1 SGK.
+ Dùng phương pháp vấn đáp cùng với HS giải vd2 như SGK.
+ Cho HS nghiên cứu vd3 rồi lên bảng trình bày.
+ Cho HS khác nhận xét và GV chính xác hoá lời giải.
+ Trả lời.
+ Nhận xét.
+ Phát biểu.
+ Lắng nghe.
+ Trả lời.
+ Nhận xét.
§2 CỰC TRỊ CỦA HÀM SỐ
I. Khái niệm cực đại, cực tiểu
Định nghĩa (SGK)
Chú ý (SGK)
II. Điều kiện đủ để hàm số có cực trị
Định lí 1 (SGK)
x
x0-h x0 x0+h
f’(x)
 + -
f(x)
 fCD
x
x0-h x0 x0+h
f’(x)
 - +
f(x)
 fCT
4. Củng cố toàn bài(3’):
+ Cho học sinh giải bài tập trắc nghiệm:
 Số điểm cực t ...  hình (H) là hình gì? 
-Các mặt của hình (H’) là hình gì?
-Nêu cách tính diện tích
+Nhìn hình vẽ trên bảng phụ xác định hình (H) và hình (H’)
+HS trả lời các câu hỏi
+HS khác nhận xét
*Bài tập 2: sgk trang 18
Giải :
Đặt a là độ dài của hình lập phương (H), khi đó độ dài cạnh của hình bát diện đều (H’) bắng 
-Diện tích toàn phần của hình (H) bằng 6a2
-Diện tích toàn phần của hình (H’) 
 của các mặt của hình (H) và hình (H’)?
-Nêu cách tính toàn phần của hình (H) và hình (H’)?
+GV chính xác kết quả sau khi HS trình bày xong
bằng
Vậy tỉ số diện tích toàn phần của hình (H) và hình (H’) là 
*Hoạt động 2: Khắc sâu khái niệm và các tính chất của khối đa diện đều
TG
Hoạt động của GV
Hoạt động của HS
Ghi bảng
10’
+GV treo bảng phụ hình vẽ trên bảng
+Hỏi: 
-Hình tứ diện đều được tạo thành từ các tâm của các mặt của hình tứ diên đều ABCD là hình nào?
-Nêu cách chứng minh G1G2G3G4 là hình tứ diện đều?
+GV chính xác lại kết quả
+HS vẽ hình
+HS trả lời các câu hỏi
+HS khác nhận xét
*Bài tập 3: sgk trang 18
 Chứng minh rằng các tâm của các mặt của hình tứ diện đều là các đỉnh của một hình tứ diện đều.
G4
A
C
D
M
B
G1
G2
G3
K
N
Giải:
Chứng minh tương tự ta có các đoạn G1G2 =G2G3 = G3G4 = G4G1 = G1G3 = suy ra hình tứ diện G1G2G3G4 là hình tứ diện đều . 
 Điều đó chứng tỏ tâm của các mặt của hình tứ diện đều ABCD là các đỉnh của một hình tứ diện đều.
Xét hình tứ diện đều ABCD có cạnh bằng a. Gọi M, N, K lần lượt là trung điểm của cạnh BC, CD, AD. Gọi G1, G2, G3, G4 lần lượt là trọng tâm của các mặt ABC, BCD, ACD, ABD. 
Ta có:
*Hoạt động 3: Giải bài tập 4 sgk trang 18
TG
Hoạt động của GV
Hoạt động của HS
Ghi bảng
5’
+Treo bảng phụ hình vẽ trên bảng
a/GV gợi ý:
-Tứ giác ABFD là hình gì?
-Tứ giác ABFD là hình thoi thì AF và BD có tính chất gì?
+GV hướng dẫn cách chứng minh và chính xác kết quả
+GV yêu cầu HS nêu cách chứng minh AF, BD và CE cắt nhau tại trung điểm của mỗi đường
+Yêu cầu HS nêu cách chứng minh tứ giác BCDE là hình vuông
+HS vẽ hình vào vở
D
A
B
C
F
E
I
+HS trả lời các câu hỏi
+HS trình bày cách chứng minh
+HS trình bày cách chứng minh
*Bài tập 4: sgk trang 18
Giải:
a/Chứng minh rằng: AF, BD và CE đôi một vuông góc với nhau và cắt nhau tại trung điểm của mỗi đường
Do B, C, D, E cách đều điểm A và F nên chúng cùng thuộc mặt phẳng trung trực của đoạn thẳng AF. Tương tự A, B, F, D cùng thuộc một phẳng và A, C, F, E cũng cùng thuộc một mặt phẳng
Gọi I là giao điểm của BD và EC. Khi đó AF, BD, CE đồng quy tại I
Ta có: tứ giác ABFD là hình thoi nên: AF^BD
Chứng minh tương tự ta có:
AF^EC, EC^BD.
Vậy AF, BD và CE đôi một vuông góc với nhau
*Tứ giác ABFD là hình thoi nên AF và BD cắt nhau tại trung điểm I của mỗi đường
-Chứng minh tương tự ta có: AF và EC cắt nhau tại trung điểm I, BD và EC cũng cắt nhau tại trung điểm I
Vậy các đoạn thẳng AF, BD, CE cắt nhau tai trung điểm của mỗi đường
b/Chứng minh: ABFD,AEFC, BCDE là những hình vuông
Do AI^(BCDE) và 
 AB = AC = AD = AE nên 
 IB = IC = ID = IE
Suy ra BCDE là hình vuông
Chứng minh tương tự ta có : ABFD, AEFC là những hình vuông
 IV. Củng cố toàn bài : (3’)
 Cho khối chóp có đáy là n-giác. Trong các mệnh đề sau đây, mệnh đề nào đúng ?
a/ Số cạnh của khối chóp bằng n+1	b/ Số mặt của khối chóp bằng 2n
c/ Số đỉnh của khối chóp bằng 2n+1	d/ Số mặt của khối chóp bằng số đỉnh của nó
 Hướng dẫn và ra bài tập về nhà : (1’)
 Nắm vững lại các định nghĩa về khối đa diện lồi, khối đa diên đều và các tính chất của nó
 Làm lại các bài tập 1,2,3,4 sgk trang 18
 Đọc bài và tìm hiểu bài mới trước ở nhà
Tiết 5 Ngµy so¹n........ .
§3.KHÁI NIỆM VỀ THỂ TÍCH CỦA KHỐI ĐA DIỆN (Tiết 1/2)
I. Mục tiêu
1. Về kiến thức:
- Nắm được khái niệm về thể tích khối đa diện
- Nắm được các công thức tính thể tích của khối hộp chữ nhật, khối lăng trụ, khối chóp.
- Biết chia khối chóp và khối lăng trụ thành các khối tứ diện (bằng nhiều cách khác nhau).
2. Về kỹ năng:
- Rèn luyện kỹ năng vận dụng các công thức tính thể tích để tính được thể tích khối hộp chữ nhật, khối chóp, khối lăng trụ.
- Kỹ năng vẽ hình, chia khối chóp thành các khối đa diện.
3. Về tư duy, thái độ:
- Vận dụng linh hoạt các công thức vào các bài toán liên quan đến thể tích.
- Phát triển tư duy trừu tượng.
- Kỹ năng vẽ hình.
II. Chuẩn bị của giáo viên và học sinh:
 Giáo viên:
 Chuẩn bị vẽ các hình 1.25; 1.26; 1.28 trên bảng phụ
 Chuẩn bị 2 phiếu học tập
 HS: Ôn lại kiến thức hình chóp, lăng trụ... đã học ở lớp 11.Đọc trước bài mới ở nhà.
III. Phương pháp:
 Nêu vấn đề, dẫn dắt đến công thức, phát vấn gợi mở, xây dựng công thức
 Phát huy tính tích cực tự giác của học sinh
 §an xen c¸c d¹ng ho¹t ®éng cña häc sinh th¶o luËn nhãm vµ 
IV. Tiến trình bài học.
Ổn định tổ chức.
Kiểm tra bài cũ (5 phút)
H1: Phát biểu định nghĩa khối đa diện, khối đa diện đều và các tính chất của chúng.
H2: Xét xem hình bên có phải là hình đa diện không? Vì sao?
Bài mới.
HĐ1: Khái niệm về thể tích khối đa diện
Hoạt động giáo viên
Hoạt động học sinh
Ghi bảng
- Đặt vấn đề: dẫn dắt đến khái niệm thể tích của khối đa diện
- Giới thiệu về thể tích khối đa diện:
Mỗi khối đa diện được đặt tương ứng với một số dương duy nhất V (H) thoả mãn 3 tính chất (SGK).
- Giáo viên dùng bảng phụ vẽ các khối (hình 1.25)
- Cho học sinh nhận xét mối liên quan giữa các hình (H0), (H1), (H2), (H3)
H1: Tính thể tích các khối trên?
- Tổng quát hoá để đưa ra công thức tính thể tích khối hộp chữ nhật.
+ Học sinh suy luận trả lời.
+ Học sinh ghi nhớ các tính chất.
+ Học sinh nhận xét, trả lời.
+ Gọi 1 học sinh giải thích V= abc.
I.Khái niệm về thể tích khối đa diện.
1.Kháiniệm(SGK)
+Hình vẽ(Bảng phụ)
 2. Định lí(SGK)
HĐ2: Thể tích khối lăng trụ
Hoạt động giáo viên
Hoạt động học sinh
Ghi bảng
H2: Nêu mối liên hệ giữa khối hộp chữ nhật và khối lăng trụ có đáy là hình chữ nhật.
H3: Từ đó suy ra thể tích khối lăng trụ 
* Phát phiếu học tập số 1
 + Học sinh trả lời:
Khối hộp chữ nhật là khối lăng trụ có đáy là hình chữ nhật.
+ Học sinh suy luận và đưa ra công thức.
+ Học sinh thảo luận nhóm, chọn một học sinh trình bày. 
Phương án đúng là : C.
II.Thể tích khối lăng trụ
 Định lí: Thể tích khối lăng trụ có diện tích đáy là B,chiều cao h là:
 V=B.h
HĐ3: Thể tích khối chóp
Hoạt động giáo viên
H động học sinh
Ghi bảng
+ Giới thiệu định lý về thể tích khối chóp
+ Thể tích của khối chóp có thể bằng tổng thể tích của các khối chóp, khối đa diện.
+ Yêu cầu học sinh nghiên cứu Ví dụ1 (SGK trang 24)
H4: So sánh thể tích khối chóp C. A’B’C’ và thể tích khối lăng trụ ABC. A’B’C’?
H5: Suy ra thể tích khối chóp C. ABB’A’?
Nhận xét về diện tích của hình bình hành ABFE và ABB’A’?
H6: Từ đó suy ra thể tích khối chóp C. ABEF theo V.
H7: Xác định khối (H) và suy ra V (H)
H8: Tính tỉ số =?
* Phát phiếu học tập số 2:
Ví dụ 2: bài tập 4 trang 25 SGK.
* Hướng dẫn học sinh giải và nhấn mạnh công thức để học sinh áp dụng vào giải các bài tập liên quan 
 + Một học sinh nhắc lại chiều cao của hình chóp. Suy ra chiều cao của khối chóp.
+ Học sinh ghi nhớ công thức.
+ Học sinh suy nghĩ trả lời: 
VC.A’B’C’= 1/3 V
VC. ABB’A’= 2/3V
 E’
SABFE= ½ SABB’A’
 =1/2
Học sinh thảo luận nhóm và nhóm trưởng trình bày.
Phương án đúng là phương án B.
VA’. SB’C’= 1/3 A’I’.SS.B’C’
VA.SBC= 1/3 AI.SSBC
III.T/t khối chóp
1. Định lý: (SGK)
 2. Ví dụ 
E’
 4.Củng cố (5’): Giáo viên hướng dẫn học sinh nhắc lại: Công thức tính thể tích khối hộp chữ nhật, khối lăng trụ, khối chóp. Phương pháp tính thể tích khối lăng trụ, khối chóp
Tiết 6 Ngµy so¹n........ .............
§3.KHÁI NIỆM VỀ THỂ TÍCH CỦA KHỐI ĐA DIỆN (Tiết 2/2)
I. Mục tiêu
1. Về kiến thức:
- Nắm được khái niệm về thể tích khối đa diện
- Nắm được các công thức tính thể tích của khối hộp chữ nhật, khối lăng trụ, khối chóp.
- Biết chia khối chóp và khối lăng trụ thành các khối tứ diện (bằng nhiều cách khác nhau).
2. Về kỹ năng:
- Rèn luyện kỹ năng vận dụng các công thức tính thể tích để tính được thể tích khối hộp chữ nhật, khối chóp, khối lăng trụ.
- Kỹ năng vẽ hình, chia khối chóp thành các khối đa diện.
3. Về tư duy, thái độ:
- Vận dụng linh hoạt các công thức vào các bài toán liên quan đến thể tích.
- Phát triển tư duy trừu tượng.
- Kỹ năng vẽ hình.
II. Chuẩn bị của giáo viên và học sinh:
 Giáo viên:
 Chuẩn bị vẽ các hình 1.25; 1.26; 1.28 trên bảng phụ
 Chuẩn bị 2 phiếu học tập
 Học sinh: Ôn lại kiến thức hình chóp, lăng trụ... đã học ở lớp 11.Đọc trước bài mới ở nhà.
III. Phương pháp:
 Nêu vấn đề, dẫn dắt đến công thức, phát vấn gợi mở, xây dựng công thức
 Phát huy tính tích cực tự giác của học sinh
 §an xen c¸c d¹ng ho¹t ®éng cña häc sinh th¶o luËn nhãm vµ 
IV. Tiến trình bài học.
Ổn định tổ chức.
Hoạt động 1 : Hướng dẫn học sinh làm bài tập củng cố lý thuyết
TG
HĐ của GV
HĐ của học sinh
Ghi bảng
10’
H:Hãy so sánh diện tích 2 tam giác BCM và BDM (giải thích).Từ đó suy ra thể tích hai khối chóp ABCM, ABMD?
H:Nếu tỉ số thẻ tích 2 phần đó bằng k,hãy xác định vị trí của điểm M lúc đó?
Yêu cầu hs trả lời đáp án bài tập số 16 SGK
Hai tam giác có cùng đường cao mà MC = 2MD
nên .Suy ra 
(vì hai khối đa diện có cùng chiều cao)
=> MC = k.MD
Bài 1 :Cho tứ diện ABCD.M là điểm trên cạnh CD sao cho MC = 2 MD.Mặt phẳng (ABM) chia khối tứ diện thành hai phần .Tính tỉ số thể tích hai phần đó.
Giải: 
 MC = 2 MD => 
=>
 Hoạt động 2: Tính thể tích của khối lăng trụ .
TG
HĐ của GV
HĐ của học sinh
Ghi bảng
10’
Yêu cầu hs xác định góc giữa đường thẳng BC’ và mặt phẳng (AA’C’C)
Gọi hs lên bảng trình bày các bước giải
Nhận xét,hoàn thiện bài giải
Yêu cầu hs tính tổng diện tích các mặt bên của hình lăng trụ ABCA’B’C’
Giới thiệu diện tích xung quanh và Yêu cầu hs về nhà làm bài 20c tương tự
Hs xác định góc giữa đường thẳng BC’ và mặt phẳng (AA’CC’)
Bài 2:Bài 19 SGK
Giải.
a)
 = 
b)
Do đó 
 Hoạt động 3: Tính tỉ số thể tích của 2 khối đa diện
TG
HĐ của giáo viên
HĐ của HS
Ghi bảng
10’
Yêu cầu hs xác định thiết diện
H: Cách tính V2?
Hướng hs đưa về tỉ số 
Hướng hs xét các tỉ số 
H: Tỉ số đồng dạng của hai tam giác SBD và SB’D’ bằng bao nhiêu?Tỉ số diện tích của hai tam giác đó bằng bao nhiêu?
H:Tỉ số chiều cao của 2 khối chóp SMB’D’ và SCBD bằng bao nhiêu?Suy ra 
Gọi hs lên bảng trình bày
Nhận xét ,hoàn thiện bài giải
Xác định thiết diện,từ đó suy ra G là trọng tâm tam giác SBD
Trả lời các câu hỏi của giáo viên
Lên bảng trình bày
Bài 3 : Bài 24 SGK
Giải. 
 Ta có .Vì B’D’// BD nên 
Gọi V1,V2,V3,V4 lần lượt là thể tích của các khối đa diện SAB’D’,SABD,SMB’D’,SCBD.
Vì hai tam giác SB’D’ và SBD đồng dạng với tỉ số nên 
Tương tự ta có (Vì tỉ số chiều dài hai chiều cao là ).Suy ra 
5 Bài tập về nhà: Giải các bài tập 1,2,3,5,6 SGK
V. Phụ lục:
1. Phiếu học tập :
a. Cho (H) là khối lăng trụ đứng tam giác đều có tất cả các cạnh bằng a, thể tích (H) bằng:
A. 	 B. 	C. D.
Bảng phụ: Vẽ các hình 1.25; 1.26 ; 1.28 trên bảng phụ 
gi¸o ¸n ®¹i sè – h×nh häc 12 c¬ b¶n c¶ n¨m chuÈn kiÕn thøc kü n¨ng míi 2011-2012
liªn hÖ ®t 01689218668
gi¸o ¸n ®¹i sè – h×nh häc 12 c¬ b¶n c¶ n¨m chuÈn kiÕn thøc kü n¨ng míi 2011-2012
liªn hÖ ®t 01689218668