Giáo án Giải tích 12 - Bài 1: Tính đơn điệu và đạo hàm của hàm số

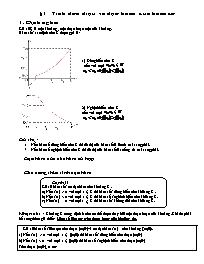
§1. Tính đơn điệu và đạo hàm của hàm số 
1. Định nghĩa
Giả sử K là một khoảng , một đoạn hoặc một nửa khoảng.
Hàm số f xác định trên K được gọi là :
1) Đồng biến trên K
 nếu với mọi 
2) Nghịch biến trên K
nếu với mọi 
Đồ thị :
Nếu hàm số đồng biến trên K thì đồ thị của hàm số đi lên từ trái sang phải.
Nếu hàm số nghịch biến trên K thì đồ thị của hàm số đi xuống từ trái sang phải.
³ Đạo hàm của các hàm số hợp
³ Các công thức tính đạo hàm
 Định lí
Giả sử hàm số f có đạo hàm trên khoảng K . 
a) Nếu f’(x) > 0 với mọi x K thì hàm số f đồng biến trên khỏang K .
b) Nếu f’(x) < 0 với mọi x K thì hàm số f nghich biến trên khỏang K.
c) Nếu f’(x) = 0 với mọi x K thì hàm số f không đổi trên khỏang K.
Nhận xét : Khoảng K trong định lí trên có thể được thay bởi một đoạn hoặc nửa khoảng .Khi đó phải bổ sung thêm giả thiết: Hàm số liên tục trên đoạn hoặc nửa khoảng đó.
 Giả sử hàm số f liên tục trên đoạn và có đạo hàm f’(x) trên khoảng .
a) Nếu f’(x) > 0 với mọi x thì hàm số f đồng biến trên đoạn 
b) Nếu f’(x) < 0 với mọi x thì hàm số f nghịch biến trên đoạn 
Trên đoạn , ta có:
HS đồng biến trên đoạn 	HS nghịch biến trên đoạn 
Ví dụ 1: Chứng minh rằng hàm số : nghịch biến trên đoạn .
Ví dụ 2: Xét chiều biến thiên của hàm số : 
Giải
Tập xác định của hàm số là .
Ta có : 
 y’ = 0 x = 2
Chiều biến thiên của hàm số được nêu trong bảng sau 
 Vậy hàm số đồng biến trên mỗi khoảng và , nghịch biến trên mỗi khoảng (2; 0) và (0; 2) .
 Xét chiều biến thiên của hàm số: 
Ví dụ 3: Xét chiều biến thiên của hàm số: 
Giải
Hàm số xác định trên .
Ta có : 
y’ = 0 với và y’ > 0 với mọi x .
Bảng biến thiên :
Vì hàm số đồng biến trên hai nửa khoảng và nên hàm số đồng biến trên .
Qua ví dụ 3 ta thấy có thể mở rộng định lí 2 như sau :
Mở rộng định lí 2: Giả sử hàm số f có đạo hàm trên khoảng K . 
a) Nếu f’(x) ≥ 0 với mọi x K và f’(x) = 0 chỉ tại một số hữu hạn điểm của K thì hàm số f đồng biến trên K .
b) Nếu f’(x) 0 với mọi x K và f’(x) = 0 chỉ tại một số hữu hạn điểm của K thì hàm số f nghịch biến trên K .
Bài 1. Chứng minh rằng
a) Hàm số nghịch biến trên mỗi khoảng xác định của nó .
b) Hàm số đồng biến trên mỗi khoảng xác đònh của nó .
c) Hàm số nghịch biến trên .
Bài 2. Chứng minh rằng hàm số đồng biến trên 
Bài 3. Với các giá trị nào của , hàm số , đồng biến trên mỗi khoảng xác định của nó?
Bài 4. Với các giá trị nào của , hàm số: 
Nghịch biến trên ?
Bài 5. Cho hàm số: 
a) Tìm đạo hàm của hàm số f .
b) Từ a) suy ra rằng hàm số f lấy giá trị không đổi trên và tính f(x) .
Bài 6. Cho hàm số xácđịnh bởi: 
a) Tìm đạo hàm của hàm số f .
b) Từ a) suy ra rằng f là một hàm hằng trên khoảng và tính f(x) .
Bài 7. Cho hàm số .
Chứng minh rằng hàm số f đồng biến trên nửa khoảng .
 Xét chiều biến thiên của hàm số: 
Bài tập cơ bản
Những bài toán có dấu * là bắt buộc
Bài 1. Xét chiều biến thiên của các hàm số sau:
Hàm bậc ba*
a) e) 
b) f) 
c) g) 
d) h) 
Hàm trùng phương*
a) c) 
b) d) 
Hàm bậc cao 
a) b) 
c) d) 
Hàm nhất biến*
a) b) 
Hàm hữu tỉ*
a) b) 
c) d) 
Hàm chứa căn thức
a) b) 
c) d) 
Bài 2.* Với các giá trị nào của a thì hàm số nghịch biến trên .
Bài 3.* Tìm các giá trị của tham số a để hàm số 
đồng biến trên .
Bài 4. Chứng minh rằng các hàm số sau đây đồng biến trên .
a) * b) 
Bài 5.* Chứng minh rằng hàm số :, nghịch biến trên .
Bài 6. Chứng minh rằng:
a) Hàm số là đồng biến trên moãi khoảng xác định của nó. 
b) Hàm số là nghịch biến trên mỗi khoảng xác định của nó
Bài tập tham khảo thêm bài giải trong sách bài tập
Bài 1. Xét chiều biến thiên của cáchàm số sau :
a) b) 
c) e) 
Bài 2. Chứng minh rằng
a) Hàm số nghịch biến trên đoạn ;
b) Hàm số đồng biến trên nửa khoảng ;