Giáo án dạy thêm Hình học 12: Mặt cầu
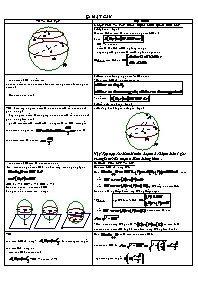
I. MẶT CẦU VÀ CÁC KHÁI NIỆM LIÊN QUAN ĐẾN M.C:
1. Mặt cầu: (sgk)
Mặt cầu (S) có tâm O, bán kỉnh r ký hiệu S(O;r )
Ta có:
+ OM = r: b.kính;
+ điểm C, D(S) CD: đgl dây cung.
+ dây cung AB qua tâm OAB đgl đường kính.
Bạn đang xem tài liệu "Giáo án dạy thêm Hình học 12: Mặt cầu", để tải tài liệu gốc về máy bạn click vào nút DOWNLOAD ở trên
§2 MẶT CẦU VD VÀ BÀI TẬP NỘI DUNG I. MẶT CẦU VÀ CÁC KHÁI NIỆM LIÊN QUAN ĐẾN M.C: 1. Mặt cầu: (sgk) Mặt cầu (S) có tâm O, bán kỉnh r ký hiệu S(O;r ) Ta có: + OM = r: b.kính; + điểm C, DÎ(S) ÞCD: đgl dây cung. + dây cung AB qua tâm OÞAB đgl đường kính. Jchú ý: m/s (S) xđ + cho đ.tròn ( C) và điểm A. khi nào điểm A thuộc đ.tròn? A nằm trong đ.tròn? nằm ngoài đ.tròn? + Hình tròn đ/n ntn? 2.Điểm nằm trong, ngoài m/c. Khối cầu: * Cho m/c S(O;r) và điểm A. ta có: * khối cầu: 3. Biểu diễn mặt cầu: (sgk) VD1: Tìm tập hợp các điểm M nhìn đoạn AB cố định dưới 1 góc vuông? + Tập hợp các điểm M trong mp nhìn đoạn AB cố định dưới 1 góc vuông? c/m ntn? + gọi O: tr.điểm AB ÞΔMAB vuông tại M có OM: tr.tuyến thuộc cạnh huyền Þ nên M thuộc m/c tâm O, b.kính . 4. Đường kinh tuyến vĩ tuyến: (sgk) Vậy “Tập hợp các điểm M nhìn đoạn AB cố định dưới 1 góc vuông là m/c (S) nhận AB làm đường kính”. + cho đ.tròn ( C) tâm O, b.kính r. đt d. Xét vị trí tương đối của (C ) và d? có mấy trường hợp? gọi .OH > r Þ ? OH= r Þ ? OH< r Þ ? Khi nào đt d tx với đ.tròn ( C)? Tươg tự đối với mặt cầu và mp. II. GIAO CỦA M/C VÀ MP: Cho m/c S(O; r) và mp (P). Gọi , ta có: + nếu + nếu mp (P) tiếp xúc m/c (S). Lúc đó: . H: đgl tiếp điểm; mp (P) đgl tiếp diện. * Chú ý: mp (P) tx m/c (S) + nếu: đ.tròn tâm H, b.k * Đặc biệt: khi mp (P) qua OÞ: có tâm là O, b.kính r nên đ.tròn (C ) đgl đ.tròn lớn và mp (P) đgl mp kính. VD2: cho m/c S(O;r) và mpa:. Xđ đ.tròn giao tuyến của m.c (S) và mp a. + tâm của (C ) x.định ntn? + = OHÞ b.kính r’ =? Gọi Þ H: tâm của đ.tròn (C ). b.kính của ( C) là: vậy đ.tròn giao tuyến III. GIAO CỦA M/C VÀ Đ.THẲNG. TIẾP TUYẾN CỦA M/C: Cho m/c S(O;r) và đt D. Gọi Gọi mp a chứa đt D và điểm O. vị trí tương đối của m/c (S) và đt D là vị trí tương đối của mpa và đt D. 1. Nếu OH > r thì 2. Nếu OH = r thì . H: tiếp điểm và đt D đgl đt tiếp tuyến của mặt cầu (S). * D tiếp xúc với (S) Û Δ ^ OH tại tiếp điểm H. 3. Nếu OH < r thì Khi D qua O thì D cắt (S) tại 2 điêm A,B. Khi đó AB là đ.kính của m/c. Nhận xét: a) điểm AÎS(O;r), ta có vô số tiếp tuyến với (S) qua A. các tiếp tuyến này đều nằm trong tiếp diện của (S) tạo A. b) điểm AÏS(O;r), ta có vô số tiếp tuyến với (S) qua A. tập hợp các tiếp tuyến này tạo ra 1 mặt nón đỉnh A. IV. CT TÍNH DIỆN TÍCH M/C VÀ THỂ TÍCH KHỐI CẦU: Cho m/c S(O;r) + Diện tích m/c là: ; +thể tích k.cầu là: Chú ý: (sgk) V. MẶT CẦU NGOẠI TIẾP ĐA DIỆN: 1. Mặt cầu đgl ngoại tiêp đa diện nếu nó đi qua các đỉnh của đa diện, đa diện đgl nội tiếp trong mặt cầu. 2. Cách xác định tâm và tính bán kính mặt cầu ngoại tiếp h.chóp: Hình chóp nội tiêp được trong mặt cầu (S) Û đa giác đáy nội tiêp được trong đường tròn. T.Quát: Gọi m/c (S) có tâm I, bán kính là r. cách xđ tâm I như sau: + Xác định trục Δ của đa giác đáy ( Δ^(đáy) tại tâm). + Dựng mp a là trung trực của 1 cạnh bên. + Þ I: tâm của mặt cầu (S) và bán kính r = IA. Các trường hợp đặc biệt: a) Hình chóp đều: cách xác định tâm I và b.kính r m/c (S) như sau: J Xác định tâm I: + Gọi O là tâm của đáy Þ SO ^ (đáy) Þ SO là trục của đa giác đáy. + Gọi H: trung điểm SA. Trong mp (SAO), dựng đt d là t.trực của SA Þ d Ç SO = I. Vì là tâm m/c (S) ngoại tiếp h/c. J Tính bán kính r = IS: ΔSHI ~ ΔSOA b) Hình chóp có 1 cạnh bên vuông góc với đáy: giả sử hình chóp S.ABC có SA^( ABC); gọi O: tâm của ΔABC J Xác định tâm I: + dựng đt Δ qua O: Δ// SA Þ Δ ^ (ABC) Þ Δ: trục của ΔABC. + Gọi H là trung điểm của SA. Trong mp (SAO) dựng đt d là trung trực của SA Þ d Ç SO = I. ( lưu ý d // AO). Vì là tâm m/c (S) ngoại tiếp h/c. J Tính bán kính r = IA: Ta có tứ giác AHIO là hình chữ nhật 3. mặt cầu đgl nội tiếp trong hình đa diện nếu m/c đó tiếp xúc với các mặt của đa diện, hình đa diện đgl ngoại tiếp mặt cầu. BÀI TẬP MẶT CẦU BÀI TẬP NỘI DUNG CÁCH TÌM TÂM VÀ TÍNH BÁN KÍNH M/C NGOẠI TIẾP ĐA DIỆN: có 4 cách xác định tâm và tính b.kính 1. Điểm I là tâm của m/c (S) ngoại tiếp đa diện Û I cách đều các đỉnh của đa diện; lúc đó r = IA. 2. Đa diện có các đỉnh cùng nhìn 1 đoạn thẳng AB dưới 1 góc vuông thì đa diện nội tiếp trong m/c (S) nhận AB làm đường kính, nên tâm I: trung điểm AB; b.kính r = AB/2. 3. Dạng h/c đều ( lý thuyết) 4. Dạng h/c có 1 cạnh bên vuông góc với đáy (lý thuyết) HD bài 2: h/c đều S.ABCD có các cạnh = a. Xđ tâm I, tính r. + Xác định tâm I gọi ABCD có tâm O, và S.ABCD là h/c đều Nên SO là trục của h/c Gọi H: tr.điểm SA, trong mp (SAO) dựng đt d là tr.trực của SA Þ d Ç SO = I thì I là tâm của m/c ng.tiếp h/c + Tính b.kính r = IS: Vì h/c đều nên ABCD là hv nên (1) Xét ΔSAO vuông tại O (2) Từ (1) và (2) Nên O là tâm m/c ngoại tiếp h/c nên nên HD bài 3;4 HD bài 5: C/m: MA.MB = MC.MD Gọi đ.tròn ( C) tâm I; bk R B’ là điểm đx của B qua I Gọi IM = d, ta có T.tự, ta có MC.MD = nên MA.MB=MC.MD b) suy ra từ câu a. HD bài 7: hhcn ABCD.A’B’C’D’ có AA’=a; AB=b; AD=c. a) Xác định tâm và tính bán kính m/c qua 8 đỉnh của hhcn? +Theo t/c hình hộp, các đ/chéo AC’, BD’, CA’, DB’ cắt nhau tại trung điểm mỗi đường. Mặt khác, hhcn ABCD.A’B’C’D’ nên AC’= BD’= CA’= DB’ Nên IA=IB=IC=ID=IA’= = IB’=IC’=ID’ Þ điểm I cách đều các đỉnh hhcn nên I là tâm m/c (S) đi qua 8 đỉnh. +Tính bán kính r = IA: ta có: độ dài đ/chéo hhcn là: b) ta có (S) Ç (ABCD) = ( C) :đ.tròn gọi ACÇBD = O Þ O là tâm hcn ABCD Þ O: tâm đ/tròn(C) nên bán kính của ( C) là R = OA= HD bài 10: + Xác định tâm I của m/c (S): Vì SA^SBÞΔSAB vuông tại S Gọi O tr.điểm AB Þ O: tâm của đ.tròn ng.tiếp ΔSAB dựng đt d qua O: d ^ (SAB) Þ d: trục của ΔSAB. Gọi H : tr.điểm SC, trong mp(SCO) dựng đt d1 là tr.trực của SC Þ d1 Ç d = I Þ I: tâm m/c (S) Þ r = IS + Tính bán kính r = SI Dễ dàng c/m được: SOIH là hcn Xét ΔSAB vuông tại S, có SO: là tr.tuyến Nên SO = Do đó, r = SI Thay vào CT diện tích và thể tich.
Tài liệu đính kèm:
 2 mat cau va bai tap( chuong 2).doc
2 mat cau va bai tap( chuong 2).doc





