Giáo án dạy thêm Hình học 12: Khái niệm về mặt tròn xoay
2. Hình nón tròn xoay, khối nón:
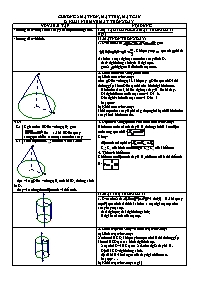
a) Hình nón tròn xoay:
cho OIM vuông tại I. khi quay OIM quanh OI thì đường gấp khúc OIM tạo thành 1 hình đgl hình nón.
+ Hình tròn tâm I, bk IM đgl mặt đáy; R=IM bk đáy.
+ OI đgl chiều cao của mặt nón và OI = h.
+ OM đgl đ/sinh của mặt nón và OM=l
+ Mặt nón:
b) Khối nón tròn xoay:
khối nón tròn xoay là phần kg được giới hạn bởi hình tròn xoay kể cả hình nón đó.
Bạn đang xem tài liệu "Giáo án dạy thêm Hình học 12: Khái niệm về mặt tròn xoay", để tải tài liệu gốc về máy bạn click vào nút DOWNLOAD ở trên
CHƯƠNG 2 MẶT NÓN, MẶT TRỤ, MẶT CẦU §1 KHÁI NIỆM VỀ MẶT TRÒN XOAY VD VÀ BÀI TẬP NỘI DUNG - hướng dẫn về mặt tròn xoay; khái niệm đường sinh. I. SỰ TẠO THÀNH CỦA MẶT TRÒN XOAY: (sgk) - hướng dẫn vẽ hình. II. MẶT NÓN TRÒN XOAY: 1. Đ/n: cho 2 đt ; góc . Khi quay mp quanh thì đt d sinh ra 1 mặt đgl mặt nón tròn xoay đỉnh O. + đt d: đgl đường sinh; đt đgl trục. + góc 2 ddgl góc ở đỉnh của mặt nón. 2. Hình nón tròn xoay, khối nón: a) Hình nón tròn xoay: cho OIM vuông tại I. khi quay OIM quanh OI thì đường gấp khúc OIM tạo thành 1 hình đgl hình nón. + Hình tròn tâm I, bk IM đgl mặt đáy; R=IM bk đáy. + OI đgl chiều cao của mặt nón và OI = h. + OM đgl đ/sinh của mặt nón và OM=l + Mặt nón: b) Khối nón tròn xoay: khối nón tròn xoay là phần kg được giới hạn bởi hình tròn xoay kể cả hình nón đó. VD: Gt Kgian cho OIM vuông tại I; góc ; IM = a. khi OIM quay xung quanh IM ta có mặt nón tròn xoay Kl Tính diện tích Sxq; thể tích V của k.nón + dựa vào OIM vuông tại I, tính bk IO, đường sinh MO. + thay vào công thức diện tích và thể tích. 3. Diện tích xung quanh của hình nón tròn xoay: Hình nón có bán kính đáy là R, đường sinh là l có diện tích xung quanh là: Chú ý: + diện tích toàn phần: + Sxq; Stp của hình nón cũng là Sxq; Stp của khối nón 4. Thể tích khối nón: Khối nón có diện tích đáy là B, chiều cao là h thì thể tích là: II. MẶT TRỤ TRÒN XOAY: 1. Đ/n: cho 2 đt và d(d;l) = R. khi quay mp(P) quanh đt d thì đt l sinh ra 1 mặt đgl mặt trụ tròn xoay hay mặt trụ. + đt d đgl trục; đt l đgl đường sinh; + R đgl bán kính của mặt trụ. 2. Hình trụ tròn xoay và khối trụ tròn xoay: a) Hình trụ tròn xoay: Xét hcn ABCD, khi quay hcn quanh AB thì đường gấp khúc ABCD tạo ra 1 hình đgl hình trụ. + 2 cạnh AD và BC tạo ra 2 đ.tròn đgl 2 đáy bk R. + Độ dài CD: đgl đường sinh. + độ dài AB: khoảng cách 2 đáy đgl chiều cao. + Mặt trụ: b) Khối trụ tròn xoay: (sgk) Sửa b.tập 5: Gt h.trụ có bk đáy r = 5 cm; khoảng cách giữa 2 đáy bằng 7cm Kl a) Tính Sxq; V b) Cắt khối trụ bởi mp (P) song song với trục và cách trục 3 cm. Tính d.tích thiết diện h.dẫn: a) + h = l = 7cm suy ra Sxq; + d.tích đáy B= r2=25suy ra thể tích. b) + vì (P) d nên thiết diện làhcn CDEF nên SCDEF = CD.DE Gọi M: tr.điểm CD Ta có: AM=3 và AMCD Dựa vào DAM suy ra DM CD=2DM; DE=AB=7 Suy ra diện tích cần tìm. 3. Diện tích và thể tích: a. Diện tích hình trụ: Hình trụ có bán kính đáy là R, đ/sinh là l có diện tích xung quanh là: + Diện tích tp: Stp = Sxq+2Sđ ; với diện tích đáy là diện tích hình tròn Sđ = B=R2 b. Thể tích khối trụ: Khối trụ có diện tích đáy là B, chiều cao là h có thể tích là: Sửa b.tập 3: (sgk) Gọi S là đỉnh của h.nón a)dùng Pitago trongSOC tính SC= = lSxq=.. b) Tính diện tích đáy B=Sh.tròn=r2V=.. c) I: tr.điểm AB mp(P) qua S SA=SB OIAB; gọi OHSI OH(SAB) OH=d(O;(P))=12. SOI vuông tại O có OH đ/cao OI = .. SI=.. SIA, tính IA AB = 2IA Vậy = Sửa b.tập 7 (sgk) a) tính + l=h=r. + diện tích đáy B=.r2. b) thay vào ct tính thể tích V=Bh= c) tính d(AB;OO’)=? gtOO’AA’ gọi H tr.điểm A’B thì OHBA’ và OHA’A OH(ABA’) d(O’O;AB) = OH. + gt góc ABA’ vuông tại A’BA’=.. +OHA’ vuông tại H có OA’= r; Suy ra độ dài OH. Hướng dẫn b.tập 6;8;9
Tài liệu đính kèm:
 1 mat non, mat tru(day them).doc
1 mat non, mat tru(day them).doc





