Giáo án dạy thêm Hình học 12: Bài tập và bài tập ôn tập chương I
BÀI TẬP VÀ BÀI TẬP ÔN TẬP CHƯƠNG I
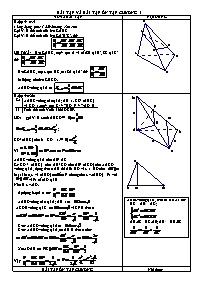
B.tập 4/ tr.5
( ứng dụng như 1 đ.lý, không cần cm)
Gọi V1 là thể tích của h/c S.ABC
Gọi V2 là thể tích của h/c S.A’B’C’. thì:
Bạn đang xem tài liệu "Giáo án dạy thêm Hình học 12: Bài tập và bài tập ôn tập chương I", để tải tài liệu gốc về máy bạn click vào nút DOWNLOAD ở trên
BÀI TẬP VÀ BÀI TẬP ÔN TẬP CHƯƠNG I VD VÀ BÀI TẬP NỘI DUNG B.tập 4/ tr.5 ( ứng dụng như 1 đ.lý, không cần cm) Gọi V1 là thể tích của h/c S.ABC Gọi V2 là thể tích của h/c S.A’B’C’. thì: HỆ QUẢ: + H/c S.ABC, mp a qua A và cắt SB tại B’, SC tại C’ thì: + H/c S.ABC, mp a qua BC, căt SA tại A’ thì: + Mở rộng cho h/c S.BCD. + ΔABC vuông tại A Þ B.tập 5/tr26: Gt ΔABC vuông cân tại A; AB=a. CD^(ABC) và CD=a. mpa qua C: aÇBD=F, aÇAD=E kl Tính thể tích V của khối DCEF. HD: + gọi V1 là t.tích ABCD Þ ; CD^(ABC) nên h = CD = a.Þ Vì ΔABC vuông tại A nên AB^AC Gt: CD ^ (ABC) nên AB^CD nên AB^(ACD) nên ΔACD vuông tại A, dựng đ/cao AH thì AH^BD và a ^ BD nên Mặt khác, a và (ABD) có điểm F chung nên aÇ(ABD) = Ft với và Ft cắt AD tại E Nên E=aÇAD. + Áp dụng h.quả ta có: + ΔABC vuông cân tại A; AB=a Þ +ΔCDB vuông tại C và CF là đ/cao + C/m: ΔACD vuông tại A Þ + C/m: ΔABD vuông tại A, có AH là đ/cao nên: + Xét ΔDAH có Vậy Þ ΔABC vuông tại A, đ/cao là AH. Ta có: + BC2 = AB2 + AC2; + + AB.AC = BC.AH; AH2 = BH.HC + BÀI TẬP ÔN TẬP CHƯƠNG Nội dung B.tập 5/tr26: Gt h/c O.ABC có OA^OB, OB^OC, OA^OC OA = a, OB = b, OC = c. kl Tính đ/cao OH của h/chóp. Gọi CH cắt AB tại I. gt Mặt khác: OH là đ/cao của h/c nên OH^AB, OH^CI Do đó AB^(OCH) Þ OI là đ/cao của ΔOAB vuông tại O, ta có Mặt khác: OC^OI nên ΔOIC vuông tại O, có OH là đ/cao nên B.tập 6/tr26: Gt h/c đều S.ABC, AB = a; cạnh bên SA tạo với đáy (ABC) 1 góc 600. mpa qua BC và a^SA; aÇSA=D kl a) Tính tỉ số thể tích của S.DBC và S.ABC b) Tính thể tích của S.BCD a)Gọi V1 là thể tích của h/c S.ABC; Gọi V là thể tích của h/c S.BCD Vì h/c đều Þ: tâm của ΔABC nên và SO^(ABC). + ΔABC đều cạnh a : và. Xét ΔSAO vuông tại O,có . Nên + ΔSAN, đ/cao ND ÞND^SA, a^SA nên Vì mp a chứa BC, cắt SA tại D nên: + xét ΔDAN vuông tại D Nên B.tập 8/tr26: Gt h/c S.ABCD có ABCD là hcn, SA^(ABCD). AB=a, AD=b, SA=c. kl Tính thể tích V k. chóp S.AB’C’D’ + Tính thể tích V1 của S.ABCD: . + Gọi E=SOÇB’D’. C’=AEÇSC thì C’=(AB’D’)ÇSC. Ta có: . + ΔABS,ΔADS vuông tại A . + C/m: + ΔSAC vuông tại A ; suy ra tỉ số B.tập 9/tr26: Gt h/c đều S.ABCD, ABCD hv cạnh a, tâm O.cạnh bên tạo với đáy 1 góc 600 Gọi M: trung điểm SC. mpa qua AM và ; aÇSB = E, aÇSD = F kl Tính thể tích V k. chóp S.AEMF +Gọi I= SOÇAM. và ItÇSB=E Þ E= SBÇa; ItÇSD=F Þ F= SDÇa + Gọi V1: thể tích S.ABCD + h/c S.ABCD đều , nên ÞΔSACđều cạnh (đ/chéo hv cạnh a) suy ra V1= + I trọng tâm ΔSBD, . + M: trung điểm SC . Suy ra tỉ số: = B.tập 10/tr27: Gt Lăng trụ đứng ABC.A’B’C’, có tất cả các cạnh là a. kl a) Tính thể tích V khối tứ diện A’BB’C. b) mpa qua A’B’ và G: trọng tâm ΔABC, aÇAC = E, aÇBC = F. tính thể tích V1 của khối chóp C.A’B’EF. a) Gọi M: trung điểm AB và (gt) Þ ΔABC đều Þ CM ^ AB mặt khác, L.t đứng ÞBB’^(ABC)Þ CM ^BB’ suy ra CM ^ (ABB’A’) + Vì L.trụ đứng nên các mặt bên là hình chữ nhật Nên SABB’A’ = AB.AA’= a2. Do đó, V= B.h với ; b) + Tính thể tích V2 L.trụ ABC.A’B’C’: V2=B.h với B=SΔABC, h= AA’. + Tính thể tích V3 h/c C.A’B’C’:với B=SΔABC, h= CC’. + Tính T.tích V4 h/c A’.ABEF: Ta có: tứ giác ABEF có EF//AB nên tứ giác ABEF là hình thang; mà CM^AB nên CG^EF nên GM là đ.cao của hình thang ABEF . với , h= AA’. + Tính thể tích V5 h/c E.A’B’B: với B=SΔA’B’B. Mp (ABC), dựng EK//MG Þ EK^(ABB’A’) nên Vậy T.tích cần tìm
Tài liệu đính kèm:
 bai tap on tap chuong 1.doc
bai tap on tap chuong 1.doc





