Giáo án Đại số và giải tích lớp 11 - Công thức lượng giác và phương trình lượng giác

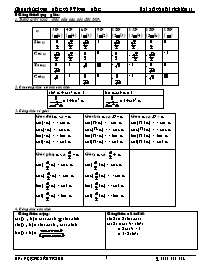
I/ C«ng thøc l­ỵng gi¸c:
1, B¶ng g/trÞ l­ỵng gi¸c cđa c¸c gãc ®Ỉc biƯt:
 α
300
(P/6)
450
(P/4)
600
(P/3)
900
(P/2)
1200
(2P/3)
1350
(3P/4)
1500
(5P/6)
1800
( P )
Sin α
1
0
Cos α
0
-
-
-
-1
Tan α
 1
////
-
-1
-
0
Cot α
 1
0
-
-1
-
////
2, C¸c c«ng thøc c¬ b¶n cÇn nhí:
sin2 α + cos2 α = 1
tan α.cot α =1
= 1+ tan2 α 
 = 1+ cot2 α
3, C«ng thøc vỊ gãc:
Gãc ®èi: α vµ - α
sin(-α) = - sin α
cos(-α) = cos α
tan(-α) = - tan α
cot(-α) = - cot α
Gãc bï: α vµ P - α
sin(P-α) = sin α
cos(P-α) = - cos α
tan(P-α) = - tan α
cot(P-α) = - cot α
Gãc: α vµ P + α
sin(P+α) = - sin α
cos(P+α) = - cos α
tan(P+α) = tan α
cot(P+α) = cot α
Gãc phơ: α vµ - α
sin(-α) = cos α
cos(-α) = sin α
tan(-α) = cot α
cot(-α) = tan α
Gãc : α vµ + α
sin(+α) = cos α
cos(+α) = -sin α
tan(+α) = -cot α
cot(+α) = -tan α
4, C«ng thøc cÇn nhí:
 C«ng thøc céng:
cos(a ± b) = cosa.cosb sina.sinb
sin(a ± b) = sina.cosb ± cosa.sinb
tan(a ± b) = 
C«ng thøc nh©n ®«i:
sin2a = 2 sina.cosa
cos2a = cos2a- sin2a
 = 2cos2a - 1
 = 1- 2sin2a
C«ng thøc h¹ bËc 2: ( §­ỵc suy ra tõ c«ng thøc nh©n ®«i).
C«ng thøc biÕn tÝch thµnh tỉng:
cosa.cosb = [cos(a+b)+ cos(a-b)]
sina.cosb = [sin(a+b)+sin(a-b)]
sina.sinb = [cos(a-b)- cos(a+b)]
C«ng thøc biÕn tỉng thµnh tÝch:
cosa + cosb = 2 cos .cos 
cosa - cosb = -2 sin .sin 
sina + sinb = 2 sin.cos
sina - sinb = 2cos.sin
tana ± tanb = 
cota ± cotb = 
Chĩ ý: mét sè ct hay dung trong biÕn ®ỉi
1+ sin2x = ( sinx + cosx)2
1- sin2x = ( sinx - cosx)2
1- cos2x = 2sin2x
1+ cos2x = 2cos2x
tanx + cotx = 
sinx + cosx = 
sinx - cosx = 
cosx- sinx = 
cos3x = 4cos3x - 3cosx
sin3x = 3sinx - 4sin3x 
 Ví dụ: Chứng minh rằng:
 1. 
 2. 
 Ví dụ: Tính , 
 Ví dụ: Rút gọn biểu thức: 
 Ví dụ: 1. Biến đổi thành tổng biểu thức: 
 2. Tính giá trị của biểu thức: 
 Ví dụ: Biến đổi thành tích biểu thức: 
II/ Ph­¬ng tr×nh l­ỵng gi¸c:
PT l­ỵng gi¸c c¬ b¶n:
1/ ph­¬ng tr×nh: sinx = m = sin α
§k ®Ĩ pt cã nghiƯm lµ: -1≤ m ≤ 1
nghiƯm cđa pt lµ: (kỴZ)
nghiƯm cđa c¸c pt ®Ỉc biƯt:
+ sinx=1 Þ x= +k2P
+ sinx=-1 Þ x= -+k2P
+ sinx= 0 Þ x= kP
- trong tr­êng hỵp m kh«ng x¸c ®Þnh ®­ỵc lµ sin cđa gãc ®Ỉc biƯt nµo, ta dïng nghiƯm
 (kỴZ)
3/ ph­¬ng tr×nh: tanx = m = tan α
- TX§: x ≠+kP (kỴZ)
nghiƯm cđa pt lµ: (kỴZ)
nghiƯm cđa c¸c pt ®Ỉc biƯt:
+ tanx=1 Þ x= +kP
+ tanx=-1 Þ x= -+kP
+ tanx= 0 Þ x= kP
- trong tr­êng hỵp m kh«ng x¸c ®Þnh ®­ỵc lµ tan cđa gãc ®Ỉc biƯt nµo, ta dïng nghiƯm
 (kỴZ)
2/ ph­¬ng tr×nh: cosx = m = cos α
§k ®Ĩ pt cã nghiƯm lµ: -1≤ m ≤ 1
nghiƯm cđa pt lµ: (kỴZ)
nghiƯm cđa c¸c pt ®Ỉc biƯt:
+ cosx=1 Þ x= k2P
+ cosx=-1 Þ x= P+k2P
+ cosx= 0 Þ x= +kP
- trong tr­êng hỵp m kh«ng x¸c ®Þnh ®­ỵc lµ cos cđa gãc ®Ỉc biƯt nµo, ta dïng nghiƯm
 (kỴZ)
4/ ph­¬ng tr×nh: cotx = m = cot α
- TX§: x ≠ kP (kỴZ)
nghiƯm cđa pt lµ: (kỴZ)
nghiƯm cđa c¸c pt ®Ỉc biƯt:
+ cotx=1 Þ x= +kP
+ cotx=-1 Þ x= -+kP
+ cotx= 0 Þ x= +kP
- trong tr­êng hỵp m kh«ng x¸c ®Þnh ®­ỵc lµ cot cđa gãc ®Ỉc biƯt nµo, ta dïng
nghiƯm
 (kỴZ)
 Ví dụ: 1) Giải các phương trình :
	 a) b) c) d) e) f) 
 2) Giải các phương trình:
 a) c) 
	 b) d) 
	 e) 
B.C¸c ph­¬ng tr×nh th­êng gỈp:
jPT thuÇn nhÊt bËc 2,bËc 3 ®èi víi mét hµm sè l­ỵng gi¸c sinx, cosx, tanx,cotx:
- Tỉng qu¸t: a.sin2x+b.sinx+c = 0 (1)
 a.sin3x+b.sin2x+c.sinx+d = 0 (2)
- C¸ch gi¶i: §Ỉt Sinx = t , ®iỊu kiƯn cđa t lµ: -1≤ t ≤1
 sau ®ã thay vµo (1) vµ (2) gi¶i pt theo Èn t , t×m x=?
C Chĩ ý: NÕu ®Ỉt t theo sin hoỈc cos th× cã ®k cđa t nh­ trªn, cßn nÕu ®Ỉt t theo tan hoỈc cot th× ®k cđa t lµ R.
 Ví dụ : giai cac phuong trinh sau:
	 a) b) 
 c) d) 
 e) f) 
 g) h) 
 k) l) 
 kPT bËc nhÊt ®èi víi sinx vµ cosx:
- Tỉng qu¸t: a.sinx + b.cosx = c (1)
- §K cÇn vµ ®đ ®Ĩ (1) cã nghiƯm lµ: a2+b2 ≥ c2
- C¸ch gi¶i:
 chia hai vÕ cđa (1) cho ta ®­ỵc pt:
 .sinx + .cosx = (2)
§Ỉt sinα = vµ cos α = 
(2) ↔ sinx.cos α + cosx. sinα = 
 ↔ sin( x+ α) = 
chĩ ý: ë pt d¹ng nµy sau khi ®­a vỊ (2) th× vµ cã thĨ lµ gi¸ trÞ lg gi¸c cđa c¸c gãc ®Ỉc biƯt nh­ ;;.
 Ví dụ : Giải các phương trình :
	 a) b) 
 c) d) 
	 e) 
 l/ PT bËc 2, bËc 3 ®èi víi sinx vµ cosx:
 - Tỉng qu¸t: a.sin2x + b.sinxcosx + c.cos2x = d (1)
 a.sin3x + b.sin2xcosx + c.cos2xsinx + d.cos3x = e( sinx+ cosx) (2)
 - C¸ch gi¶i:
 + xÐt cosx= 0 Þ sinx = ±1 cã thoa m·n (1) hay kh«ng, nÕu cã th× nghiƯm cđa pt lµ: 
x= +kP
+ xÐt cosx≠ 0, chia c¶ h¸i vÕ (1) cho cos2x, ta ®­a vỊ pt bËc 2, bËc 3 theo tanx
 sau ®ã ®Ỉt tanx = t, t×m t =? Þ x= ?
Chĩ ý: trong PT d¹ng nµy ta ph¶i dïng c«ng thøc: = 1+ tan2 α
Ví dụ : Giải phương trình:
	 a;
 b; 
 c; 
mPT d¹ng: 
 - Tỉng qu¸t: a.( sinx ± cosx) + b. sinxcosx = c (1)
 - C¸ch gi¶i:
 §Ỉt sinx ± cosx = t , §K cđa t lµ: 
 Þ sinxcosx = (2)
 sau ®ã thay vµo (1) gi¶i PT vµ t×m t=?
 thay t vµo (2) cã sin2x= ± (t2-1) Þ x=?
 Ví dụ : Giải phương trình :
Ví dụ : Giải phương trình : 	a. 
b. 
nPh­¬ng ph¸p kh¸c:
DẠNG 1: C¸c ph­¬ng ph¸p hay dïng:
PPhương pháp 1: Biến đổi pt đã cho về một trong các dạng pt lượng giác cơ bản đã biết 
 Ví dụ: Giải phương trình:
P Phương pháp 2: Biến đổi pt đã cho về dạng tích số 
 Cơ sở của phương pháp là dựa vào các định lý sau đây:
 hoặc 
 Ví dụ : Giải các phương trình :
	a. b. 
	c. d. 
	e, (sinx+1)(2 sinx+1)= cosx
PPhương pháp 3: - Dïng c«ng thøc h¹ bËc:
 - Dïng c«ng thøc nh©n ®«i: 
Ví dụ : Giải các phương trình :
	a. 	b. 
	c. d. 
PPhương pháp 4: Dïng c«ng thøc biÕn tỉng thµnh tÝch:
Ví dụ : Giải các phương trình
a, cos3x+cos5x = sin2x-sin6x	 b, sin4x+cos5x= sinx + cos2x
c, tan2x+tan3x = sin5x	 d, sin2x+ sin6x- cos8x=-1	
PPhương pháp 5: Dïng CT biÕn tÝch thµnh tỉng:
Ví dụ : Giải các phương trình
a, cosx.cos5x = sin2x.sin6x	 b, sin4x.cos5x + sinx = cos2x
c, tan2x.tan3x -1= cos5x	 d, sin2x+ sin6x- cos8x=-1	
PPhương pháp 6: PT theo tanx vµ cotx:
Ví dụ : Giải các phương trình
a, 	b, 
	c, d, tanx- cotx= sinx +cosx e, 3(tanx+cotx) = 2(2+sin2x)
F Bµi TËp tù luyƯn:
 Bài 1: Giải các phương trình lượng giác sau
	1) 2) 
	3) 
	4) 5) 
	6) 
Bài 2 : Giải các phương trình lượng giác sau
	1. 8. 
	2. 9. 
	3. 10. 
	4. 11. 
	5. 12. 
	6. 13. 
 7. 14. 
DẠNG 2: Phương trình lượng giác có chứa tham số
Sử dụng phương pháp sau
Chọn ẩn phụ thích hợp và tìm điều kiện đúng cho ẩn phụ vừa chọn (tùy thuộc vào x)
Chuyển phương trình về phương trình đại số 
Lập luận để chuyển bài toán đã cho theo ẩn phụ vừa chọn
Sử dụng phương pháp giải tích hoặc đại số để tìm tham số theo yêu cầu của đề bài
Bài 1: Tìm m để phương trình sau có nghiệm:
Bài 2: Định m để phương trình : 
 có nghiệm 
Bài 3: Cho hàm số: 
 Tìm m để phương trình có nghiệm thuộc 
Bài 4: Cho phương trình : 
 Tìm tất cả các giá trị của m để phương trình có nghiệm.
Bài 5: Xác định m để phương trình :
 có ít nhất một nghiệm thuộc đoạn 
Bài 6: Cho phương trình : (1)
 Tìm tất cả các giá trị của m để phương trình (1) có nghiệm.
Bài 7: Tìm m để phương trình : có nghiệm.
Bài 8: Cho phương trình 
 Định m để phương trình có nghiệm .
Bài 9: Tìm m để phương trình : 
 có nghiệm trên đoạn 
Bài 10: Cho phương trình: 
 Với giá trị nào của m thì phương trình có nghiệm
Bài 11: Cho phương trình: 
 Với giá trị nào của m thì phương trình có nghiệm
Bài 12: Tìm m để phương trình : có nghiệm
( cßn nhiỊu d¹ng bµi tËp n÷a, t¸c gi¶ sÏ cËp nhËt sau)