Giáo án Đại số 10 tiết 13, 14: Hàm số bậc hai

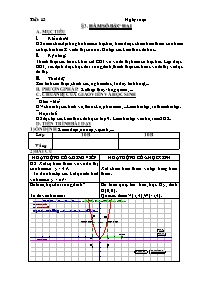
Tieát 13 Ngaøy soaïn: 
§3. HÀM SỐ BẬC HAI
MỤC TIÊU
Kieán thöùc: 
HS nắm chắc định nghĩa hàm số bậc hai, hiểu được chiều biến thiên của hàm số bậc hai trên R và đồ thị của nó. Ôn tập các kiến thức đã hoc.
Kyõ naêng:
Thành thạo các bước khảo sát CBT và vẽ đồ thị hàm số bậc hai. Lập được BBT, xác định được trục đối xứng, đỉnh, thành thạo các bước vẽ đồ thị và đọc đồ thị. 
Thaùi ñoä:
Rèn tính cẩn thận, chính các, nghiêm túc, tư duy linh hoạt, ...
PHƯƠNG PHÁP: Kết hợp thầy-trò, gợi mở, ...
CHUẨN BỊ CỦA GIÁO VIÊN VÀ HỌC SINH
* Giaùo vieân:
GV chuẩn bị các hình vẽ, thước kẻ, phấn màu, ...Làm bài tập, ra thêm bài tập.
* Hoïc sinh:
HS đọc lại các kiến thức đã học ở lớp 9. Làm bài tập về nhà, xem SGK.
TIẾN TRÌNH BÀI DẠY
1) ỔN ĐỊNH: Kiểm diện, nề nếp, vệ sinh,....
Líp
10B
10B
	V¾ng
2) BÀI CŨ: 
HO¹T §éng cña gi¸o viªn
HO¹T §éng cña häc sinh
HS: Xét sự biến thiên và vẽ đồ thị của hàm số: y = 4x2.
 Từ đó nhắc lại các kết quả đã biết về hàm số: y = ax2.
Xét chiều biến thiên và lập bảng biến thiên.
Bề lõm, trục đối xứng, đỉnh?
Từ đó vào bài mới:
Bề lõm quay lên trên, trục Oy, đỉnh O(0; 0).
Qua các điểm V(1; 4), W(-1; 4).
3) NỘI DUNG BÀI MỚI:
Ho¹t ®éng thÇy vµ trß
Néi dung kiÕn thøc
HĐ1. Định nghĩa: 
Hàm số bậc hai là hàm số cho bởi công thức y = ax2 + bx + c (a≠0)
1. Định nghĩa: 
Mở rộng công thức y = ax2 (thêm các hệ số b và c) đã học ở lớp 9.
HĐ 2. Đồ thị của hàm số bậc hai.
HĐ1.1. Nhận xét: 
H1> Đỉnh O(0; 0) có vị trí như thế nào đối với các điểm khác:
 khi a > 0, 
khi a < 0?
2. Đồ thị của hàm số bậc hai.
§ỉnh O(0; 0) thấp nhất khi a > 0;
 cao nhất khi a < 0.
2) Ta có: y = ax2 + bx + c =
 a(x + b/2a)2 + (-D/4a). D = b2 – 4ac.
H> Khi a > 0: giá trị nhỏ nhất của y?
H> Khi a < 0: giá trị lớn nhất của y?
H> Khi x = -b/2a Þ y = ?
H> Vai trò của I đối với đồ thị của hàm số : y = ax2 + bx + c như thế nào so với vai trò của O trong đồ thị y = ax2?
HĐ1.2. Đồ thị:
Nhận xét: Đồ thị 
 y = ax2 + bx + c chính là parabol sau khi dịch chuyển.
Kết luận: 
 Đồ thị h/ số y = ax2 + bx + c (a ≠ 0) là mét đường parabol có đỉnh 
I(-b/2a;-D/4a), có trục đối xứng là đường thẳng x = -b/2a. Parabol quay bề lõm lên trên khi a > 0, xuống dưới khi a < 0.
* y ≥ -D/4a ; "x Î R.
* y ≤ -D/4a ; "x Î R.
Ngoài ra I(-b/2a; -D/4a) Î đồ thị của hàm số.
 Vai trò của I đối với đồ thị của hàm số: y = ax2 + bx + c như vai trò của O trong đồ thị y = ax2.
Đồ thị h/số y = ax2 + bx + c (a ≠ 0) là một đường parabol có đỉnh 
I(-b/2a; -D/4a), có trục đối xứng là đường thẳng x = -b/2a. Parabol quay bề lõm lên trên khi a > 0, xuống dưới khi a < 0.
HĐ1.3. Cách vẽ: 
H> Nêu các yếu tố cần xác định khi vẽ đồ thị của hàm số bậc hai?
Ví dụ: Vẽ parabol y = 3x2 -2x – 1.
B1. Xác định đỉnh I(-b/ 2a; -D/4a).
B2. Vẽ trục đối xứng x = -b/ 2a. (qua đỉnh và // hoặc trùng Oy)
B3. Xác định các giao điểm với trục Oy (điểm C(0; c)) và trục Ox, các điểm đặc biệt khác.
B4. Vẽ parabol. (Chú ý dấu của a)
 Đỉnh I (1/3; -4/3); trục đối xứng x = 1/3; Giao với Oy là: C(0; -1)
Đồ thị đi qua C’(2/3; -1)
Giao với Ox là A(1; 0) và B(-1/3; 0).
HĐ2. Chiều biến thiên của hàm số bậc hai.
H> Dựa vào đồ thị hãy kết luận về chiều biến thiên?
H> Đọc từ bảng biến thiên?
Định lí: 
 Nếu a > 0 thì hàm số nghịch biến trên khoảng (- ∞; -b/2a), đồng biến trên khoảng (-b/2a; +∞)
 Nếu a < 0 thì hàm số đồng biến biến trên khoảng (- ∞; -b/2a), nghịch trên khoảng (-b/2a; +∞).
2. Chiều biến thiên của hàm số bậc hai.
Khi a > 0: 
x
- ∞ -b/2a + ∞ 
y
-D/4a
+∞ + ∞ 
Khi a < 0.
X
- ∞ -b/2a +∞ 
y
-D/4a
-∞ - ∞ 
4) CŨNG CỐ - HƯỚNG DẪN VỀ NHÀ:
* Hs đọc lại SGK, nắm chắc các kiến thức đã học. 
* Làm bài tập SGK; SBT. * Đọc bài đọc thêm.
Tieát 14 Ngaøy soaïn: 
§3. Bài tập: HÀM SỐ BẬC HAI.
MỤC TIÊU
Kieán thöùc: 
HS cũng cố các tính chất của hàm số bậc hai (sự biến thiên, đồ thị.)
Kyõ naêng:
HS áp dụng được các tính chất của hàm số vào các bài toán: Vẽ đồ thị, lập bảng biến thiên, xác định các tính chất của hàm số và đồ thị của nó. Thành thạo trong việc vẽ đồ thị.
Biết vận dụng để giải một số bài tập.
Thaùi ñoä:
Rèn tính cẩn thận, nghiêm túc, tư duy linh hoạt,.... 
Biết gắn toán học vào thực tiễn cuộc sống.
PHƯƠNG PHÁP: Kết hợp thầy-trò, gợi mở, ...
CHUẨN BỊ CỦA GIÁO VIÊN VÀ HỌC SINH
* Giaùo vieân:
GV chuẩn bị các hình vẽ, thước kẻ, phấn màu, ... Làm bài tập, ra thêm ví dụ.
* Hoïc sinh:
HS đọc trước bài học, ôn lại các kiến thức đã học, chuẩn bị MTBT, thước kẻ, Làm bài tập về nhà, xem lại SGK.
TIẾN TRÌNH BÀI HỌC
1) ỔN ĐỊNH: Kiểm diện, nề nếp, vệ sinh,....
Líp
10B
10B
	V¾ng
2) BÀI CŨ: 
HO¹T §éng cña gi¸o viªn
HO¹T §éng cña häc sinh
Xác định toạ độ của đỉnh và các giao điểm của đồ thị với các trục toạ độ (nếu có) 
a) y = x2 – 3x + 2. 
b) y = - x2 + 4.
BT 1(tr:49-SGK)
a) Đỉnh I(3/2; -1/4). Giao với Oy C(0; 2)
Giao với Ox A(1; 0), B(2; 0).
b) Đỉnh I(0; 4), Giao với Oy I(0; 4).
Giao với Ox A(2; 0), A’(-2; 0).
 Lồng vào các HĐ trong giờ học.
3) NỘI DUNG BÀI MỚI:
Ho¹t ®éng thÇy vµ trß
Néi dung kiÕn thøc
HĐ 1. Lập bảng biến thiên và vẽ đồ thị của các hàm số.
HS1Øa) y = 3x2 – 4x + 1
HS2Ø b)y = - 3x2 + 2x – 1.
BT 2(tr:49-SGK)
LËp b¶ng biÕn thiªn vµ vÏ ®å thÞ cña c¸c hµm sè :
a)y = 3x2 – 4x + 1 ; b) y = - 3x2 + 2x – 1
c) y= 4x2 - 4x +1 ; d) y = -x2 +4x - 4 
e) y = 2x2 +x +1 ; f) y = -x2 +x -1
a) + §Ønh I ( 2/3; - 1/3)
HĐ 2: Gọi 2 học sinh thực hiện các bài tập:
 Xác định parabol y = ax2 + bx + 2, biết rằng parabol đó 
HS1Ø đi qua điểm A(3; -4) và có trục đối xứng là x = -3/2.
HS2Ø có đỉnh I(2; -2).
HS3Ø đi qua điểm B(-1; 6) và tung độ của đỉnh là – 1/4.
BT 3(tr:49-SGK)
 Xác định parabol y = ax2 + bx + 2, biết rằng parabol đó 
a) §i qua 2 ®iÓm M( 1; 5) & N( -2; 8)
b) §i qua ®iÓm A( 3;-4) & cã T§X x=-3/2
c) Cã ®Ønh I( 2; -2)
d) §i qua B( -1; 6) & tung ®é ®Ønh lµ - 1/4 
TXĐ: R
 3b) Đồ thị hàm số: y = ax2 + bx + 2 đi qua điểm: 
 A(3; -4) khi -4 = a.9 + b3 + 2 
hay 3a + b = -2. (1) 
 Đồ thị hàm số có trục đối xứng x = -3/2 nên –b/2a = -3/2 Û b = 3a. (2) 
Từ (1) và (2) suy ra: a = -1/3 và b = -1.
 Vậy a = -1/3 và b = -1.
3c) Parabol có đỉnh I(2; -2) 
Û và y(2) = -2 
Û b = - 4a (1) và 2a + b = - 2 (2)
 Giải hệ ta được: a = 1 và b = - 4.
3d) Đồ thị hàm số: y = ax2 + bx + 2 đi qua điểm: 
 B(-1; 6) Û 6 = a - b + 2 
hay a - b = 4. (1) 
Parabol có tung độ đỉnh – D/4a = -1/4 
Û b2 – 8a = a Û b2 = 9a (2) 
Giải hệ ta có a = 16, b = 12
 hoặc a = 1, b = - 3.
4) CŨNG CỐ - HƯỚNG DẪN VỀ NHÀ:
* Hs đọc lại SGK, nắm chắc các kiến thức đã học. Xem lại SGK.
* Làm bài tập SGK; SBT. Xem SGK, SBT nâng cao. Làm bài tập còn lại.
* Làm bài tập ôn tập chương 2.
 Chuẩn bị kiểm tra 1 tiết.
	+ T×m tËp x¸c ®Þnh cña hµm sè: 
	+XÐt tÝnh ch½n lÎ : 	
	+Kh¶o s¸t vµ vÏ ®å thÞ :