Đề thi thử đại học Toán 11
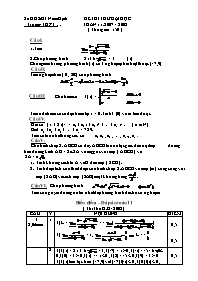
Giả sử: ( 1 + 2x )n = a0 + a1x + a2x2 + + an xn . ( n N )
Biết: a0 + a1 + a2 + + an = 729.
Tìm số lớn nhất trong các số: a0 , a1 , a2 , , an-1 , an .
Bạn đang xem tài liệu "Đề thi thử đại học Toán 11", để tải tài liệu gốc về máy bạn click vào nút DOWNLOAD ở trên
Sở GD&ĐT Nam Định ĐỀ THI THỬ ĐẠI HỌC Trường THPT . TOÁN 11. 2007 - 2008 ( Thời gian: 150’ ) CâuI. 1. Tìm: 2. Cho phương trình: 2x + 6 = 3 (1) Chứng minh rằng phương trình (1) có 3 nghiệm phân biệt thuộc (-7;9) CâuII. Tìm nghiệm trên ( 0 ; ) của phương trình: CâuIII. Cho hàm số : f(x) = Tìm a để hàm số có đạo hàm tại x = 0. Tính f’(0) với a tìm được. CâuIV. Giả sử: ( 1 + 2x )n = a0 + a1x + a2x2 + + an xn . ( n N ) Biết: a0 + a1 + a2 + + an = 729. Tìm số lớn nhất trong các số: a0 , a1 , a2 , , an-1 , an . Câu V. Cho hình chóp S. ABCD có đáy ABCD là nửa lục giác đều nội tiếp đường tròn đường kính AD = 2a. SA vuông góc với mp’ ( ABCD ) và SA = a. Tính khoảng cách từ A và B đến mp’ ( SCD ). Tính diện tích của thiết diện của hình chóp S.ABCD với mp’() song song với mp’( SAD) và cách mp’(SAD) một khoảng bằng . Câu VI. Cho phương trình: Tìm số nguyên dương n nhỏ nhất để phương trình đã cho có nghiệm. Biểu điểm – Đáp án toán 11 ( Thi Thử Đ.H- 2008 ) CÂU Ý NỘI DUNG ĐIÊM I 2,0điểm 1 +) L = = - [] +) = 1, L = - 0,5 0,5 2 +) f(x) = 2x + 6 - 3; f(-7) = 1> 0, f(-1) = -5 - 6 0, f(1) = - 1 0 +) f(x) liên tục trên (-7;9) và f(-7)f(-1) < 0, f(0)f(1) < 0, f(2)f(9) < 0. Nên f(x) = 0 hay PT đã cho có 3 nghiệm phân biệt (-7;9) 0,5 0,5 II 1,5điểm +) PT : cos2x – sin2x = - 2cosx +)cos(2x+) = cos(- x) x = (1) hoặc x = - (2) +) vì x ( 0, ) nên PT có 3 nghiệm: x1 = 0,5 0,5 0,5 III 1,5điểm +) Để f(x) có đạo hàm tại x = 0 thì f(x) phải liên tục tại x = 0, a = +) Khi a = - thì y = f(0 + x) – f(x) = +) f’(0) = - Vậy a = - thì hàm số có đạo hàm tại x = 0 và f’(0) = - . 0,5 0,5 0,5 IV 1,0điểm +) x = 1 3n = a0 + a1 + a2 + + an = 729 n = 6 và ak = , 0 ≤ k ≤ n . +) k N: Với k ≤ 3 thì (ak) đơn điệu tăng, k ≥ 4 thì (ak) đơn điệu giảm = 240 = a4 0,5 0,5 V 3,0điểm 1 +) Từ (gt) AD//BC , AB = BC = CD = a,AC CD, AB BD , AC = BD = a +)mp’(SCD) mp’(SAC) mp’(SCD)mp’(SAC) = SC.Trong mp’(SAC) : vẽ AH SC tại H , suy ra: AH = d(A;mp’(SCD) = a +)Gọi I là trung điểm AD BI // mp’(SCD) d(B,(SCD)) = d(I,(SCD)) = 0,5 0,5 0,5 2 +) Vẽ AE BC tại E AE mp’(SAD), AE = +) mp’() // mp’(SAD) và d((), (SAD)) = mp’() cắt hình chóp S.ABCD theo thiết diện MNPQ qua trung điểm K của AE + Thiết diện là hình thang vuông ( MN // PQ, MQ MN ) S = (MN + PQ).MQ. MN = Vậy: S = 0,5 0,5 0,5 VI 1,0điểm +) Nhận xét: Chỉ cần xét x > 1. CM: > 0 PT đã cho vô nghiêm +) n = 5, f(x) = liên tục trên [1; +∞) và f(1).f(1,2) < 0 sao cho f(x0) = 0 PT đã cho có nghiệm. Vậy: n = 5. 0,5 0,5
Tài liệu đính kèm:
 Bai tap on thi TN va Dai Hoc hoac lop 12 co dap an hot.doc
Bai tap on thi TN va Dai Hoc hoac lop 12 co dap an hot.doc





