Đề tham khảo thi học kì I Toán lớp 12 (Đề 14)

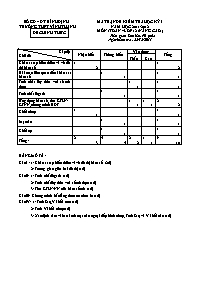
 SỞ GD – ĐT BÌNH ĐỊNH
TRƯỜNG THPT VĨNH THẠNH
ĐỀ CHÍNH THỨC
MATRẬN ĐỀ KIỂM TRA HỌC KỲ I
NĂM HỌC 2011-2012
 MÔN :TOÁN –LỚP 12 (NÂNG CAO )
 Thời gian làm bài: 90 phút 
Ngày kiểm tra : 22/12/2011
 Cấp độ
Chủ đề
Nhận biết
Thông hiểu
Vận dụng
Tổng
Thấp
Cao
Khảo sát sự biến thiên và vẽ đồ thị hàm số
1
2
1
2
Bài toán liên quan đến khảo sát hàm số
1
1
1
1
Tính chất lũy thừa với số mũ thực
1
1
1
1
Tính chất lôgarit
1
1
1
1
Ứng dụng hàm số , tìm GTLN-GTNN,chứng minh BĐT
1
1
1
1
2
2
Khối chóp
1
1
1
1
Mặt cầu
1
1
1
1
Khối trụ
1
1
1
1
Tổng :
2
3
4
4
2
2
1
1
9
10
BẢNG MÔ TẢ :
Câu I : 1/ Khảo sát sự biến thiên và vẽ đồ thị hàm số (2đ)
	2/ Tương giao giữa hai đồ thị (1đ)
Câu II: 1/ Tính chất lôgarit (1đ)
	2/ Tính chất lũy thừa với số mũ thực (1đ)
	3/ Tìm GTLN-NN của hàm số mũ (1đ)
Câu III: Chứng minh bất đẳng thức co chứa ln (1đ)
Câu IV: 1/ Tính Sxq,V khối nón (1đ)
	2/ Tính V khối chóp (1đ)
	3/ Xác định tâm và bán kính mặt cầu ngoại tiếp hình chóp, Tính Sxq và V khối cầu (1đ)
 SỞ GD – ĐT BÌNH ĐỊNH
TRƯỜNG THPT VĨNH THẠNH
ĐỀ CHÍNH THỨC
ĐỀ KIỂM TRA HỌC KỲ I-NĂM HỌC 2011-2012
 MÔN :TOÁN –LỚP 12 (NÂNG CAO )
 Thời gian làm bài: 90 phút 
Ngày kiểm tra : 22/12/2011
Câu I: (3điểm)
	Cho hàm số (1)
Khào sát sự biến thiên và vẽ đồ thị hàm số (1)
Tìm m để phương trình : có 4 nghiệm phân biệt 
Câu II:(3 điểm)
Rút gọn biểu thức : 
2) Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số : trên đoạn 
Câu III:(1 điểm)
	Chứng minh rằng với mọi ta luôn có : 
Câu IV:(3điểm)
1) Cắt một hình nón bởi mặt phẳng đi qua trục của nó, ta được thiết diện là tam giác có một góc bằng 1200 và đường cao thuộc góc đó có độ dài bằng a . Tính diện tích xung quanh hình nón đó và thể tích khối nón tương ứng .
2) Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B; góc .Hai mặt phẳng và cùng vuông góc với đáy còn mặt hợp với đáy một góc 600.
Tính thể tích khối chóp S.ABC
Tính diện tích mặt cầu ngoại tiếp hình chóp S.ABC
-------Hết------
Họ và tên thí sinh :..
Số báo danh :.
SỞ GIÁO DỤC VÀ ĐÀO TẠO BÌNH ĐỊNH
TRƯỜNG THPT VĨNH THẠNH
NĂM HỌC : 2011-2012
ĐÁP ÁN-THANG ĐIỂM
ĐỀ KIỂM TRA HỌC KÌ I 
MÔN TOÁN -LỚP 12-NC
ĐÁP ÁN-THANG ĐIỂM
Câu
Đáp án
Điểm
1
1. Khảo sát sự biến thiên và vẽ đồ thị hàm số : 
a)TXĐ : D=R
b)Sự biến thiên :
BBT
x
 0 
y’
 + 0 - 0 + 0 -
y
 4 4 
 -5 
Hàm số đồng biến trên các khoảng :; Hàm số nghịch biến trên các khoảng 
c)Đồ thị : Qua các điểm 
0.25
0.25
0.25
0.25
0.25
0.25
0.5
Câu I
2)Tìm m để phương trình : có 4 nghiệm phân biệt 
1
Số nghiệm của (*) là số giao điểm hai đồ thị và 
Dựa vào đồ thị phương trình có bốn nghiệm phân biệt khi : 
0.25
0.25
0.5
Câu II
1-a) 
1
0.25
0,5
0.25
Câu II
1-b)
1
0.25
0.25
0.25
0.25
Câu II
2) Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số : trên đoạn 
1
Vậy : ;
0.25
0.25
0.25
0.25
Câu III
Chứng minh rằng với mọi ta luôn có : 
1
Vì . Khi đó : 
Xét hàm số : trên , ta có :
Hàm số đồng biến trên nên thì đồng biến trên thì 
 (đpcm)
0.25
0.25
0.25
0.25
Câu IV
1/ Cắt một hình nón bởi mặt phẳng đi qua trục của nó, ta được thiết diện là tam giác có một góc bằng 1200 và đường cao thuộc góc đó có độ dài bằng a . Tính diện tích xung quanh hình nón đó và thể tích khối nón tương ứng .
1
Gọi thiết diện qua trục là tam giác cân ASB có góc ASB=1200 S
Tam giác vuông SOB có : 
Do đó a
 A O B
0.25
0.25
0.25
0.25
a
Hai mặt phẳng (SAB) và (SAC) cùng vuông góc với mặt phẳng (ABC) suy ra SA vuông góc với mặt phẳng (ABC)
 2) S
 A C
 B
0.25
0.25
0.25
0.25
b
2/ Mặt cầu ngoại tiếp hình chóp S.ABC có tâm là trung điểm cạnh SC, bán kính 
0.25
0.5
0.25
------Hết------
Mọi cách giải khác, nếu đúng vẫn cho điểm tối đa
SỞ GIÁO DỤC VÀ ĐÀO TẠO BÌNH ĐỊNH
TRƯỜNG THPT VĨNH THẠNH
NĂM HỌC : 2011-2012
ĐÁP ÁN-THANG ĐIỂM
ĐỀ KIỂM TRA HỌC KÌ I 
MÔN TOÁN -LỚP 12-NC
ĐÁP ÁN-THANG ĐIỂM
Câu
Đáp án
Điểm
1
1. Khảo sát sự biến thiên và vẽ đồ thị hàm số : 
2
a)TXĐ : D=R
b)Sự biến thiên :
BBT
x
 0 
y’
 - 0 + 0 - 0 +
y
 -5 
 4 4
Hàm số đồng biến trên các khoảng :; Hàm số nghịch biến trên các khoảng 
c)Đồ thị : Qua các điểm 
0.25
0.25
0.25
0.25
0.25
0.25
0.5
Câu I
2)Tìm m để phương trình : có 4 nghiệm phân biệt 
1
Số nghiệm của (*) là số giao điểm hai đồ thị và 
Dựa vào đồ thị phương trình có bốn nghiệm phân biệt khi : 
0.25
0.25
0.5
Câu II
1-a) 
1
0.25
0,5
0.25
Câu II
1-b)
1
0.25
0.25
0.25
0.25
Câu II
2) Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số : trên đoạn 
1
Vậy : ;
0.25
0.25
0.25
0.25
Câu III
Chứng minh rằng với mọi ta luôn có : 
1
Vì . Khi đó : 
Xét hàm số : trên , ta có :
Hàm số đồng biến trên nên thì đồng biến trên thì 
 (đpcm)
0.25
0.25
0.25
0.25
Câu IV
1/ Cắt một hình nón bởi mặt phẳng đi qua trục của nó, ta được thiết diện là tam giác có một góc bằng 1200 và đường cao thuộc góc đó có độ dài bằng a . Tính diện tích xung quanh hình nón đó và thể tích khối nón tương ứng .
1
Gọi thiết diện qua trục là tam giác cân ASB có góc ASB=1200 S
Tam giác vuông SOB có : 
Do đó a
 A O B
0.25
0.25
0.25
0.25
a
Hai mặt phẳng (SAB) và (SAC) cùng vuông góc với mặt phẳng (ABC) suy ra SA vuông góc với mặt phẳng (ABC)
 2) S
 A C
 B
0.25
0.25
0.25
0.25
b
2/ Mặt cầu ngoại tiếp hình chóp S.ABC có tâm là trung điểm cạnh SC, bán kính 
0.25
0.5
0.25
------Hết------
Mọi cách giải khác, nếu đúng vẫn cho điểm tối đa