Đề kiểm tra Toán 11 học kì II (dùng cho loại đề kiểm tra tự luận)

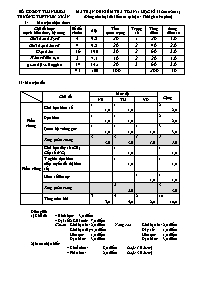
SỞ GD&ĐT THANH HÓA
MA TRẬN ĐỀ KIỂM TRA TOÁN 11 HỌC KÌ II (2010-2011)
TRƯỜNG THPT NHƯ XUÂN
(Dùng cho loại đề kiểm tra tự luận - Thời gian 90 phút)
Ma trận nhận thức:
Chủ đề hoặc 
mạch kiến thức, kỹ năng
Số tiết chuẩn
tỉ lệ
Tầm 
quan trọng
Trọng 
số
Tổng 
điểm
thang 
điểm 10
Giíi han d·y sè
4
9.8
20
1
20
1.0
Giíi h¹n hµm sè
4
9.8
20
2
40
2.0
§¹o hµm
16
39.0
30
2
60
3.0
Hµm sè liªn tôc
3
7.3
10
2
20
1.0
quan hÖ vu«ng gãc
14
34.1
20
3
60
3.0
41
100
100
200
10
II- Ma trận đề:
Chủ đề
Mức độ
Cộng
NB
TH
VD
Phần chung
Giới hạn hàm số
1
1,0
1
1,0
2
2,0
Đạo hàm
1
	1,0
1
	1,0
2
2,0
Quan hệ vuông góc
1
	1,0
1
	1,0
1
 1,0
3
3,0
Tổng phần chung
3
3,0
3
3,0
1
	1,0
7
7,0
Phần riêng
Giới hạn dãy số (CB)
Cấp số (NC)
1
1,0
1
1,0
Ý nghĩa đạo hàm
(tiếp tuyến đồ thị hàm số)
1
 1,0
1
 1,0
Hàm số liên tục
1
 1,0
1
1,0
Tổng phần riêng
2
2,0
3
3,0
Tổng toàn bài
3
3,0
5
5,0
2
 2,0
10
10,0
	Diễn giải:
	1) Chủ đề	– Hình học:	3,0 điểm
	– Đại số & Giải tích:	7,0 điểm	
	Chuẩn	+ Giới hạn hs:	2,0 điểm 	Nâng cao:	+ Giới hạn hs:	2,0 điểm
	+ Giới hạn dãy:1,0 điểm	+ Dãy số:	1,0 điểm	+ Liên tục: 	1,0 điểm	+ Liên tục:	1,0 điểm
	+ Đạo hàm:	3,0 điểm	+ Đạo hàm:	3,0 điểm
	2) Mức nhận biết:
	– Chuẩn hoá:	8,0 điểm	(hoặc 7,0 điểm)
	– Phân hoá:	2,0 điểm	(hoặc 3,0 điểm)
Mô tả chi tiết:
I. Phần chung:
	Câu 1 (2đ): Tính giới hạn của hàm số .
	Câu 2 (2đ): Tính đạo hàm của hàm số.
	Câu 3 (3đ): Bài toán hình học không gian.
II. Phần riêng:
 1) Theo chương trình chuẩn
Câu 4a (1đ): Tìm giới hạn của dãy số.
Câu 5a (1đ): Viết phương trình tiếp tuyến của đồ thị hàm số tại một điểm thuộc đồ thị.
Câu 6a (1đ): Tìm điều kiện để hàm số liên tục tại một điểm hoặc xét tính liên tục của hàm số trên 	tập xác định của nó hoặc ứng dụng tính liên tục của hàm số để chứng minh sự tồn tại nghiệm của phương trình.
 2) Theo chương trình nâng cao
	Câu 4b (1đ): Cấp số cộng, cấp số nhân hoặc tìm giới hạn của dãy số.	
Câu 5b (1đ): Viết phương trình tiếp tuyến của đồ thị hàm số với hệ số góc cho trước.
Câu 6b (1đ): Tìm điều kiện để hàm số liên tục tại một điểm hoặc xét tính liên tục của hàm số trên 	tập xác định của nó hoặc ứng dụng tính liên tục của hàm số để chứng minh sự tồn tại nghiệm của phương trình.
SỞ GD&ĐT THANH HÓA
ĐỀ KIỂM TRA HỌC KÌ II NĂM HỌC 2010-2011
TRƯỜNG THPT NHƯ XUÂN
MÔN TOÁN KHỐI LỚP 11
Thời gian làm bài: 90 phút (không kể thời gian giao đề)
I. Phần chung (7 điểm)
Câu 1 (2đ). Tính giới hạn hàm số:
	a) ;	b) .
Câu 2 (2đ). Tính đạo hàm của các hàm số sau:
	a) ;	b) .
Câu 3 (3đ). Cho hình chóp tứ giác S.ABCD có đáy ABCD là hình vuông và SA (ABCD), SA = , AB = .
a) Chứng minh các mặt bên của hình chóp S.ABCD là những tam giác vuông.
b) Tính góc giữa hai đường thẳng AB và SC.
c) Tính khoảng cách giữa hai đường thẳng SC và BD.
II. Phần riêng (3 điểm)
(Học sinh học theo chương trình nào thì làm đúng phần dành cho chương trình đó)
A. Theo chương trình chuẩn
Câu 4a (1đ). Tính giới hạn dãy số:	.
Câu 5a (1đ). Viết phương trình tiếp tuyến của đồ thị hàm số tại điểm M(1; 2).
Câu 6a (1đ). Xét tính liên tục của hàm số tại điểm .
B. Theo chương trình nâng cao
Câu 4b (1đ). Cho hai dãy số và xác định bởi
 và .
Chứng minh dãy số là một cấp số nhân và tìm .
Câu 5b (1đ). Viết phương trình tiếp tuyến của đồ thị hàm số , biết tiếp tuyến đó vuông góc với đường thẳng .
Câu 6b (1đ). Xét tính liên tục của hàm số tại điểm .
---------------------------------------------------Hết----------------------------------------------------
ĐÁP ÁN ĐỀ KIỂM TRA HỌC KÌ II NĂM HỌC 2010-2011
MÔN TOÁN KHỐI LỚP 11
Câu
Nội dung
Điểm
I. Phần chung (7 điểm)
1
(2 điểm)
a) .	
1
b) 
0.5
0.5
2
(2 điểm)
a) .	
1
b) 
0.5
0.5
3
(3 điểm)
0.5
a) V× nªn , do ®ã c¸c tam gi¸c lµ c¸c tam gi¸c vu«ng ®Ønh A.
0.5
Theo gi¶ thiÕt, ta cã:
 nªn tam gi¸c vu«ng ®Ønh B. T­¬ng tù, ta cã:
 nªn tam gi¸c vu«ng ®Ønh D.
0.5
b) Ta cã nªn .
0.25
Trong tam gi¸c SAD vu«ng ®Ønh A cã SA = , AD = nªn SD = .
Trong tam gi¸c SCD vu«ng ®Ønh D ta cã nªn . Do ®ã .
VËy: .
0.5
c) Gäi O lµ t©m cña h×nh vu«ng ABCD. Trong tam gi¸c SAC dùng .
DÔ thÊy nªn . VËy OK lµ ®­êng vu«ng gãc chung cña SC vµ BD.
0.25
Ta cã nªn .
VËy .
0.5
II. Phần riêng (3 điểm)
A. Theo chương trình chuẩn
4a
(1 điểm)
0.5
 .
0.5
5a
(1 điểm)
Ta có .
0.5
Tiếp tuyến của đồ thị hàm số tại điểm M(1; 2) có hệ số góc bằng nên có phương trình là hay .
0.5
6a
(1 điểm)
Ta có: và .
0.5
Vì nên hàm số f(x) gián đoạn tại điểm .
0.5
B. Theo chương trình nâng cao
4b
(1 điểm)
Ta có .
0.25
Suy ra dãy số là một cấp số nhân với công bội và .
0.25
Số hạng tổng quát của cấp số nhân là .
0.25
Do đó nên 
0.25
5b
(1 điểm)
Ta cã .
Gäi lµ tiÕp tuyÕn cÇn t×m vµ lµ täa ®é tiÕp ®iÓm. Khi ®ã cã hÖ sè gãc .
MÆt kh¸c, v× vu«ng gãc víi ®­êng th¼ng nªn .
0.25
Do ®ã: .
0.25
Víi nªn tiÕp tuyÕn cã ph­¬ng tr×nh lµ: hay .
0.25
Víi nªn tiÕp tuyÕn cã ph­¬ng tr×nh lµ: hay .
VËy cã hai tiÕp tuyÕn tháa m·n yªu cÇu bµi to¸n lµ vµ.
0.25
6a
(1 điểm)
Ta có: .
Mặt khác,
;
0.25
 .
0.25
Vì nên .
0.25
Suy ra .
Vậy hàm số f(x) liên tục tại điểm.
0.25
------------------------------------Hết------------------------------------