Đề kiểm tra thử môn Toán Lớp 12 học kì II (Có đáp án) - Năm học 2017-2018 - Trường THPT Trần Văn Ơn

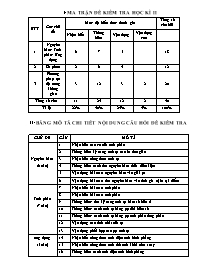
I/ MA TRẬN ĐỀ KIỂM TRA HỌC KÌ II
STT
Các chủ đề
Mức độ kiến thức đánh giá
Tổng số câu hỏi
Nhận biết
Thông hiểu
Vận dụng
Vận dụng cao

1
Nguyên hàm- Tích phân- Ứng dụng
6
7
5

18
2
Số phức
2
6
4

12
3
Phương pháp tọa độ trong không gian
3
12
3
2
20
Tổng số câu
11
25
12
2
50
Tỉ lệ
22%
50%
24%
4%
100%

II/ BẢNG MÔ TẢ CHI TIẾT NỘI DUNG CÂU HỎI ĐỀ KIỂM TRA
CHỦ ĐỀ
CÂU
MÔ TẢ
Nguyên hàm
(6 câu)
1
Nhận biết các t/c của tích phân
2
Thông hiểu kỹ năng tính tp các hs đơn giản
3
Nhận biết công thức tính tp
4
Thông hiểu cách tìm nguyên hảm thỏa điều kiện
5
Vận dụng bài toan nguyên hàm vào giải pt
6
Vận dụng bài toán tìm nguyên hàm vào tinh giá trị hs tại điểm
Tích phân
(7 câu)
 
7
Nhận biết bài toán tích phân
8
Nhận biết bài toán tích phân
9
Thông hiểu: rèn kỷ năng tính tp hàm số hửu tỉ
10
Thông hiểu: cách tính tp bằng pp đổi biến số
11
Thông hiểu: cách tính tp bằng pp tích phân từng phần
12
Vận dụng các tình chất của tp
13
Vận dụng phối hợp các pp tính tp
ứng dụng
(5 câu)

14
Nhận biết công thức tính diện tích hình phẳng
15
Nhận biết công thức tính thể tích khối tròn xoay
16
Thông hiểu cách tính diện tích hình phẳng
17
Thông hiểu cách tính thể tích khối tròn xoay
18
Vận dụng bài toán tích phân vào thực tế
Số phức
(12 câu)
19
Nhận biết số phức liên hợp
20
Thông hiểu cách tính mô đun của số phức
21
Thông hiểu cách tìm tập hợp điểm biểu diễn số phức
22
Nhận biết cách tính toán trên số phức
23
Thông hiểu cách tìm tập hợp điểm biểu diễn số phức
24
Thông hiểu cách tìm số phức thỏa điều kiện
25
Thông hiểu cách tìm hai số thực x,y thỏa đk
26
Thông hiểu cách tìm hai số thực x,y thỏa đk
27
Vận dụng tìm số phức thỏa điều kiện
28
Vận dụng tìm tập hợp điểm biểu diễn số phức
29
Vận dụng biểu diễn hh của số phức vào tính diện tích tam giác
30
Vận dụng tính toán số phức có mũ cao
Không gian
Oxyz
(20 câu)
31
Thông hiểu cách lập pt mặt phẳng
32
Nhận biết vecto pháp tuyến của mặt phẳng
33
Thông hiểu viết pt mặt phẳng theo đoạn chắn
34
Nhận biết vecto chỉ phương của đường thẳng
35
Thông hiểu pt đường trung tuyến của tam giác
36
Thông hiểu viết pt chính tắc của đường thẳng
37
Vận dụng tìm pt đường thẳng thỏa nhiều đk
38
Thông hiểu cách lập pt mặt cầu có đường kính
39
Nhận biết tâm và bán kính mặt cầu có pt cho trước
40
Thông hiểu lập pt mc có tâm và tiếp xúc với mặt phẳng
41
Thông hiểu điều kiện 3 điểm thẳng hàng
42
Thông hiểu tính thể tích khối chóp
43
Thông hiểu góc giữa 2 vecto
44
Vận dụng lập pt mp thỏa đk
45
Thông hiểu 2 đường thẳng cắt nhau
46
Thông hiểu góc giữa 2 đường thẳng
47
Thông hiểu khoảng cách từ 1 điểm đến mặt phẳng
48
Vận dụng lập pt mặt phẳng thỏa đk
49
Vận dụng cao tìm tọa độ điểm thỏa đk
50
Vận dụng cao tìm vecto chỉ phương của đường thẳng thỏa đk
Trường THPT Trần Văn Ơn ĐỀ KIỂM TRA THỬ HỌC KÌ II NH: 2017-2018
Tổ: Toán- Tin MÔN: TOÁN LỚP 12
Câu 1 Cho hàm số f (x) xác định trên R và có 1 nguyên hàm là F(x) . Cho các mệnh đề sau : 
Nếu thì 
Trong số các mệnh đề trên , số mệnh đề là mệnh đề SAI là : 
A.0 B. 1 C. 2 D. 3 
Câu 2 . Nguyên hàm của hàm số f (x) = là : 
A. B. 
C. D. 
 Câu 3.Hàm số F(x) = lnx là nguyên hàm của hàm số nào sau đây trên ( 0 ; +∞) ? 
A.f(x) = B. f(x) = 
C. f(x) = D. f(x) = 
 Câu 4 .Giá trị tham số m để hàm số F (x) = mx3 + (3m + 2 )x2 – 4x + 3 là 1 nguyên hàm của hàm số f (x) = 3x2 + 10 x – 4 là : 
A.Không có giá trị m B. m = 0 C. m = 1 D. m = 2 
 Câu 5. Biết F (x) là một nguyên hàm của f(x) =(2x -3 )lnx và F(1) =0 . Khi đó phương trình 2F(x) + x2 -6x + 5 =0 có bao nhiêu nghiệm ? 
A. 1 B. 4 C. 3 D. 2 
Câu 6. Cho F (x) là một nguyên hàm của f(x) = thỏa F (0) = 0 . Tính F ( ).
A. F B. C. F( D. F( ) = 
Câu 7: Cho . Tính theo .
A. . B. . C. J=29 tana D. .	
Câu 8: Tính .
A. .	B. .	C. .	D. 
Câu 9: Tính tích phân .
A. .	B. .	C. . D. 
Câu 10: Tính .
A. 	B. .	C. .	D. .
Câu 11: Biết , với . Chọn khẳng định đúng trong các khẳng định sau:
A. . B. . C. a+b=-7 D. .
Câu 12: Cho , và . Tính bằng.
A. . B. . C. D . .
Câu 13:Tính tích phân: được kết quả . Tổng là.
A. .	B. 1	C. .	D. .
Câu 14: Gọi S là diện tích hình phẳng được giới hạn bởi đồ thị hàm số y = f(x) ( liên tục trên ) , trục hoành Ox và hai đường thẳng x = a , x = b (a < b ) . Khi đó S được tính theo công thức nào sau đây ? 
A. S = B. S = C. S = D. S = 
Câu 15: Cho hình ( D) giới hạn bởi các đường y = f(x) , y = 0 , x = , x = e . Quay (D) quanh trục Ox ta được khối tròn xoay có thể tích V. Khi đó V được xác định bằng công thức nào sau đây ? 
A.V = B. V = C. D. 
 Câu 16: Diện tích hình phẳng giới hạn bởi hai đồ thị hàm số y = -2x3 + x2 + x + 5 và y = x2 –x + 5 bằng : 
A.S =0 B.S = 1 C.S = D.S = 
Câu 17: Tính thể tích vật thể tròn xoay khi quay hình phẳng (H) giới hạn bởi đồ thị hàm số y = , trục hoành , đường thẳng x =1 , x = 4 quanh Ox .
A.V = ln256 B. V = 12 C. S = 12 D. S = 
Câu 18: Một chất điểm chuyển động trên trục Ox với vận tốc thay đổi theo thời gian v (t) = 3t2 – 6t ( m/s). Tính quãng đường chất điểm đó đi được từ thời điểm t1 = 0 đến t2 = 4 (s) . 
A. 16 m B. m C. 96 m D. 24m 
Câu 19: Số phức liên hợp của số phức z = -1 + 2i là số phức :
A. A. z = 2-i B.z = -2 + i C. z = 1-2i D. z = -1-2i
Câu 20: Cho hai số phức z1= 6 + 8i , z2 = 4 + 3i . Khi đó giá trị | z1 – z2| là:
 A.5 B. 29 C.10 D.2
Câu 21: Điểm biểu diễn của số phức z = m + mi với m nằm trên đường thẳng có phương trình là :
A. y= 2x B.y = 3x C.y =4 x D.y= x
Câu 22: Thu gọn z= ( 2-3i)(2 +3i) ta được: 
 A.z=4 	 B.z=13	C.z= --9i	 D.z=4 –9i
Câu 23:Tập hợp các điểm trong mặt phẳng biểu diễn cho số phức z thỏa mãn điều kiện | z –i|= 1 là : 
 A.Một đường thẳng B.Một đường tròn 
 C. Một đoạn thẳng D.Một hình vuông
Câu 24 : Tìm số phức z biết |z| = 20 và phần thực gấp đôi phần ảo
 A.z1=4+3i,z2=3+4i B. z1 = 2—i,z2= -2 +i
 C.z1= -2+i ,z2= -2 –i D.z1=4+2i,z2= -4 –2i
Câu 25:Cho x,y là các số thực. Hai số phức z =3+i và z =( x +2y ) –yi bằng nhau khi:
A.x=5,y= -1	B.x=1,y=1	C.x=3 ,y=0 	D.x=2,y=-1
Câu 26 :Cho x,y là các số thực.Số phức z= 1 + xi +y +2i bằng 0 khi :
 A.x=2 ,y=1	 B.x=-2,y=-1 C. x= 0,y=0 D.x=-2,y= -2
Câu 27: Có bao nhiêu số phức z thỏa : 
 A.0	 B.1 C. 2	 D. 3
Câu 28:Tập hợp điểm M biểu diễn số phức z thỏa điều kiện : |z +1-i|=|z+3-2i| là:
A. Đường thẳng B.Elip C.Đoạn thẳng D.Đường tròn
Câu 29 : Trên mặt phẳng phức ,gọi A,B lần lượt là các điểm biểu diễn 2 nghiệm phương trình:z2-4z +13 =0.Diện tích tam giác OAB là:	
 A.16	 B.8	 C.6	 D.2
Câu 30 :Phần thực của số phức (1+i)30 bằng :
A. 0 B.1 C.215 D.-215
Câu 31: Trong không gian với hệ tọa độ , cho điểm và đường thẳng . Viết phương trình mặt phẳng đi qua điểm và vuông góc với đường thẳng .
A. .	B. .
C. .	D. .
Câu 32: Trong không gian với hệ tọa độ , mặt phẳng song song với hai đường thẳng , . Vectơ nào sau đây là vectơ pháp tuyến của ?
A. . B. . C. . D. .
Câu 33: Mặt phẳng đi qua ba điểm . Phương trình của mặt phẳng là:
A..	B..
C..	D..
Câu 34: Trong không gian cho đường thẳng . Trong các vectơ sau vectơ nào là vectơ chỉ phương của đường thẳng .
A.. B.. C..D..
Câu 35: Trong không gian với hệ tọa độ , cho tam giác có . Viết phương trình đường trung tuyến của tam giác .
A..	B..
C..	D..
Câu 36: Trong không gian với hệ tọa độ cho là đường thẳng đi qua và vuông góc với mặt phẳng . Viết phương trình chính tắc của đường thẳng .
A..	B..
C..	D..
Câu 37:Trong không gian với hệ tọa độ cho điểm và hai đường thẳng.
Viết phương trình đường thẳng đi qua điểm vuông góc với đường thẳng và cắt đường thẳng 
A. .	 B. .
C. .	D. .
Câu 38: Trong không gian với hệ tọa độ cho hai điểm và Viết phương trình mặt cầu đường kính .
A. .	B. .
C. .	D. .
Câu 39: Trong không gian với hệ toạ độ , cho mặt cầu . Mặt cầu có tâm và bán kính là.
A. .	B. .
C. .	D. .
Câu 40: Mặt cầu có tâm và tiếp xúc với mặt phẳng .
A. . B. .
C. . D. .
Câu 41: Cho ba điểmvà. Với giá trị nào của thì, , thẳng hàng?
 A. . 	B. .	C. .	D. .
Câu 42:Cho bốn điểm,,vàthể tích của tứ diện bằng .Giá trị của là.
 A. hoặc .	 B..	 C..	 D..
Câu 43:Tìm để góc giữa hai vectơ là góc nhọn.
A.. 	B.hoặc. C..	 D..
Câu 44:Trong không gian với hệ tọa độ,cho hai đường thẳng và.Phương trình nào dưới đây là phương trình đường thẳng thuộc mặt phẳng chứavà,đồng thời cách đều hai đường thẳng đó.
A..	B..
C..	D..
Câu 45:Trong không gian với hệ tọa độcho hai đường thẳng vàTìm giá trị của đểcắt .
A..	B..	C..	D..
Câu 46:Trong không gian với hệ trục tọa độ gọi là giao tuyến của hai mặt phẳng có phương trình lần lượt là và Tính số đo độ góc giữa đường thẳng và trục.
A..	B..	C..	D..
Câu 47:Trong không gian với hệ tọa độ ,cho mặt phẳng và hai điểm .Gọilần lượt là khoảng cách từ điểm và đến mặt phẳng .Trong các khẳng định sau khẳng định nào đúng?
A..	B..	C..	D..
Câu 48:Trong không gian với hệ tọa độ,cho mặt cầu .Viết phương trình mặt phẳngchứa cắt mặt cầu theo thiết diện là đường tròn có chu vi bằng .
A..	B..
C..	D..
Câu 49: Trong không gian với hệ trục tọa độ ,cho mặt phẳng và đường thẳng . Tam giác có, các điểm , nằm trên và trọng tâm nằm trên đường thẳng . Tọa độ trung điểm củalà.
A.. B.. C.. D..
Câu 50: Trong không gian với hệ toạ độ , cho đường thẳng nằm trong mặt phẳng đồng thời đi qua điểm và cắt đường thẳng . Một vectơ chỉ phương của là.
A. B. C. D.
.HẾT
ĐÁP ÁN
Câu
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
Đáp án
C
A
A
C
D
C
C
D
D
A
C
C
B
C
D
B
B
A
D
Câu
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
Đáp án
B
D
B
B
D
A
B
D
A
C
A
D
B
C
D
A
D
D
C
Câu
39
40
41
42
43
44
45
46
47
48
49
50







Đáp án
C
D
D
A
B
A
D
A
B
D
D
D








Hướng dẫn giải
Câu 1 ( Mức độ 1)
Đáp án : C ( 1 và 3 sai )
Câu 2 : ( Mức độ 2 )
Đáp án : A 
Vì 
Câu 3 : ( Mức độ 1 )
Đáp án : A 
Vì ( lnx)/ = 
Câu 4 ( Mức độ 2 )
Đáp án : C 
Ta có F/(x) = f (x)nên ta có 3m = 3 và 2 (3m + 2) = 10 .Suy ra m = 1 .
Câu 5. ( Mức độ 3 )
Đáp án : D 
Dùng phương pháp nguyên hàm từng phần ta tính được : 
F (x) = ( x2 -3x) lnx 
Phương trình đã cho trở thành ( x2 -3x )lnx =0 nên có nghiệm x = 1 , x= 3 ( do x = 0 không thỏa mãn ) .
Câu 6.( Mức độ 4 )
Đáp án C 
Lời giải : F(x) = 
Đặt u = x , dv = , ta có du = dx , v = tanx 
Suy ra F (x) = xtanx = 
Từ F (0)= 0 , ta có C = 0 .
Vây F (x) = xtanx + . Do đó F( ) = 0 .
Câu 7: Chọn C
Ta có .
Câu 8: Chọn D
.
Câu 9: Chọn D
.
Câu 10: Chọn A
Ta có: .
Câu 11:Chọn C
Câu 12: Chọn C
.
.
Câu 13: Chọn B 
Đặt .
Đổi cận : .
Vậy .
Do đó .
Câu 14 .( Mức độ 1 )
Đáp án : C 
Công thức S = chỉ đúng khi phương trình f(x) = 0 không có nghiệm thuộc khoảng (a ; b) hoặc nghiệm thuộc khoảng (a ;b ) là nghiệm bội chẵn . Hay nói cách khác , chỉ áp dụng công thức này khi f(x) chỉ mang một dấu trên đoạn .
Câu 15 . ( Mức độ 1 )
Đáp án D 
Dựa vào công thức tính thể tích khối tròn xoay với e < nên ta có 
Câu 16.( Mức độ 2 )
 Đáp án : B
Phương trình hoành độ giao điểm : -2x3 +x2 + x + 5 = x2 – x + 5 
Có các nghiệm x = -1 , x =0 , x =1 
S = 
Câu 17 ( Mức độ 2 )
Đáp án : B
Vì 
Câu 18 ( Mức độ 3 )
Đáp án : A 
Lời giải : 
Áp dụng công thức S = 
Câu 19:( NB) 
Phương án đúng là D 
Giải: số phức z =a + bi=> số phức liên hợp là a-- bi
Câu 20: (NB) 
Phương án đúng là B
HD: Tính hiệu và sử dụng công thức tính mô đun 
Câu 21: (NB) 
Phương án đúng là D
HD: vì số phức z được biểu diễn là điểm có tọa độ (m;m)
 Câu 22:  (NB)
Phương án đúng là B
HD :áp dụng công thức tìm tích 2 số phức
Câu 23: (TH)
Phương án đúng là B
HD: số phức z =a + bi ,thay vào vế trái và sử dụng công thức mô đun
Câu 24 : (TH) 
Phương án đúng là D
HD:Ap dụng công thức tính mô đun của z
Câu 25(TH):
Phương án đúng là A 
HD :Sử dụng tính chất 2 số phức bằng nhau
Câu 26(TH) : 
Phương án đúng là B 
HD :Sử dụng tính chất số phức =0 khi phần thực bằng 0 và phần ảo bằng 0
Câu 27(VD):Có bao nhiêu số phức Z thỏa : 
 A.0	 B.1 C. 2	 D. 3
Phương án đúng là D.
Câu 28(VD):
Phương án đúng là A
HD:Thay z= a+bi vào 2 vế và sử dụng công thức tính độ dài
Câu 29 (VD)
Phương án đúng là C
HD:Tìm nghiệm pt và biểu diễ n hệ trục tọa độ
Câu 30(VD):
Phương án đúng là A
HD:tách (1+i)30=[(1+i)2]15	
Câu 31.
Chọn D.
Bán kính mặt cầu là .
Phương trình của mặt cầu là .
Câu 32.
Chọn B.
Đường thẳng có vectơ chỉ phương là .
Mặt phẳng đi qua điểm và vuông góc với nên nhận làm vectơ pháp tuyến có phương trình: .
Câu 33.
Chọn C.
Phương trình theo đoạn chắn:
.
Câu 34.
 Chọn D
Câu 35.
Chọn A.
Ta có là trung điểm của nên .
.
Đường thẳng đi qua và có một vectơ chỉ phương là .
Vậy phương trình đường .
Câu 36.
Chọn D.
.
Câu 37.
Chọn D.
Giả sử .
.
 có VTCP .
.
Đường thẳng đi qua có VTCP có phương trình là:
.
Câu 38.
Chọn C.
Theo đề ta có mặt cầu đường kính có tâm là trung điểm của và bán kính .
Nên phương trình mặt cầu là: .
Câu 39
Chọn C.
Mặt cầu (với ).
có tâm , bán kính .
Câu 40.
Chọn D.
Bán kính mặt cầu là .
Phương trình của mặt cầu là 
Câu 41: Chọn D.
Tacó:.
thẳnghàng.
Câu 42: Chọn A.
Tacó,,.
Suyra.
Dođó.
.
Câu 43: Chọn B.
Để.
..
.Kế thợp điều kiện
Câu 44: Chọn A.
Ta nhận thấy đường thẳngcần tìm và,cùng thuộc mặt phẳng..
Tacó:cách đều nênnằm giữa..
Dođó:Gọi.
Trung điểmlàsẽ thuộc đường thẳngcầntìm.
Ta thếlần lượt vào các đáp án nhận thấy đáp án A thỏa.
Câu 45: Chọn D.
Giảsử
.
.
Câu 46: ChọnA.
Hai mặt phẳng vuông góc với lần lượt có các vectơ pháp tuyến là và nên đường thẳng có vectơ chỉ phương là:. 
Trục có vectơ chỉ phương là .
.
Đây là góc nhọn nên góc giữavà trục cũng bằng .
Câu 47: Chọn B.
.
Câu 48: Chọn D.
có tâm ,bán kính .Đường tròn thiết diện có bán kính .
mặt phẳngqua tâm .
chứa.
.
Chọn.
Câu 49: ChọnD.
Vì.
Giả sử ,.
Vì là trọng tâm nên ta có:.
Vậy trung điểm của đoạn là.
Do,nằm trênnên.
Câu 50: Chọn D.
Cách1:
Gọilà giao điểm củavà.
,VTPTcủalà.
Tacó:.
.Vậy.
.
Cách2:
Gọi.
.
.
./.