Đề kiểm tra lớp 12 - Môn Toán chương I: Ứng dụng đạo hàm để khảo sát và vẽ đồ thị hàm số

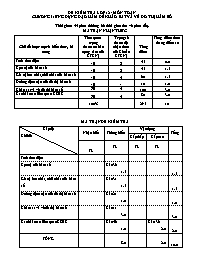
ĐỀ KIỂM TRA LỚP 12 - MÔN TOÁN
CHƯƠNG I: ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ HÀM SỐ
Thời gian: 45 phút (không kể thời gian thu và phát đề).
MA TRẬN NHẬN THỨC
Chủ đề hoặc mạch kiến thức, kĩ năng
Tầm quan trọng
(Mức cơ bản trọng tâm của KTKN)
Trọng số
(Mức độ nhận thức của Chuẩn KTKN)
Tổng điểm
Tổng điểm theo thang điểm 10
Tính đơn điệu 
15
3
45
0.0
Cực trị của hàm số 
15
3
45
1.5
Giá trị lớn nhất, nhỏ nhất của hàm số 
15
4
60
1.5
Đường tiệm cận của đồ thị hàm số
10
1
10
1.0
Khảo sát và vẽ đồ thị hàm số
25
4
100
3.0
Các bài toán liên quan KSHS
20
4
80
3.0
100%
295
10
MA TRẬN ĐỀ KIỂM TRA
Cấp độ
Chủ đề
Nhận biết
Thông hiểu
Vận dụng
Tổng
Cấp thấp
Cấp cao
TL
TL
TL
TL
Tính đơn điệu 
Cực trị của hàm số 
Câu 3b
 1.5
1.5
Giá trị lớn nhất, nhỏ nhất của hàm số 
Câu 3a
 1.5
1.5
Đường tiệm cận của đồ thị hàm số
Câu 2a
1.0
1.0
Khảo sát và vẽ đồ thị hàm số
Câu 1a 
3.0
3.0
Các bài toán liên quan KSHS
Câu 4b
 1.0
Câu 3b
 2.0
2.0
TỔNG
 8.0
 2.0
10.0
BẢNG MÔ TẢ TIÊU CHÍ LỰA CHỌN CÂU HỎI, BÀI TẬP
Câu 1a. Khảo sát sự biến thiên và vẽ đồ thị hàm số
Câu 1b. Dựa vào đồ thị đã vẽ biện luận số nghiệm phương trình. Tương giao giữa đồ thị và đường thẳng dạng đơn giản. 
Câu 2a.Viết phương trình các đường tiệm cận của đồ thị hàm số phân thức (nhất biến)
Câu 2b. Tương giao giữa đồ thị và đường thẳng, tìm tham số để đường thẳng cắt đồ thị tại ba điểm phân biệt thỏa mãn điều kiện cho trước.
Câu 3a. Tìm giá trị lớn nhất, nhỏ nhất của hàm số đa thức trên một đoạn.
Câu 3b. Tìm điều kiện để hàm số đạt cực trị tại 1 điểm, tìm điều kiện để hàm số có cực trị 
 ĐỀ CHÍNH THỨC
TRƯỜNG THPT NGUYỄN VĂN CỪ KIỂM TRA 1 TIẾT MÔN ĐẠI SỐ 12 – CHƯƠNG I
	 	 	 Năm học: 2011 – 2012 
 ĐỀ 01	 Thời gian làm bài: 45 phút (không kể thời gian giao đề)
Câu 1(4,0 điểm):
 Cho hàm số 
 Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số.
 Dùng đồ thị (C) hãy tìm tất cả các số thực m để phương trình sau có 4 nghiệm thực phân biệt.
Câu 2(3,0 điểm): 
Viết phương trình các đường tiệm cận của đồ thị (H): 
Cho hàm số (Cm).Tìm tất cả các giá trị của tham số m 
để đường thẳng (d): cắt đồ thị (Cm)tại ba điểm phân biệt A, B và C(0; 1) sao cho .
Câu 3(3,0 điểm): 
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số:
 trên đoạn [0; 2].
Tìm m để hàm số đạt cực đại tại x = 1.
---------------------HẾT----------------------
Họ và tên học sinh:Lớp
 ĐỀ CHÍNH THỨC
TRƯỜNG THPT NGUYỄN VĂN CỪ KIỂM TRA 1 TIẾT MÔN ĐẠI SỐ 12 – CHƯƠNG I
	 	 	 Năm học: 2011 – 2012 
 ĐỀ 02	 Thời gian làm bài: 45 phút (không kể thời gian giao đề)
Câu 1(4,0 điểm):
 Cho hàm số 
 Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số.
 Dùng đồ thị (C) hãy tìm tất cả các số thực m để phương trình sau có 4 nghiệm thực phân biệt.
Câu 2(3,0 điểm): 
Viết phương trình các đường tiệm cận của đồ thị (H): .
 Cho hàm số (Cm).Tìm tất cả các giá trị của tham số m 
để đường thẳng (d): cắt đồ thị (Cm) tại ba điểm phân biệt A, B và C(0; 1) sao cho .
Câu 3(3,0 điểm): 
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số:
 trên đoạn [0; 2].
Tìm m để hàm số đạt cực tiểu tại x = 1
----------------------HẾT----------------------
Họ và tên học sinh:Lớp
ĐÁP ÁN 
ĐỀ 01
Câu
Nội dung
Điểm
1
a)
1. Tập xác định D = R
2. Sự biến thiên:
Chiếu biến thiên: 
Giới hạn: 
Bảng biến thiên:
x
 -2 0 2 
y’
	-	0	+	0	-	0	+
y
Kết luận các khoảng đồng biến, nghịch biến và cực trị của hàm số
3. Đồ thị 
0,25
3x0,25
0,25
0,75
0,25
0,75
b/ PT: có 4 nghiệm phân biệt khi đường thẳng (d): y = m +1 cắt đồ thị (C) tại 4 điểm phân biệt, dựa vào đồ thị ta có: 
0,5
0,5
2
a/ ; y = -2 là đường tiệm cận ngang
 ; x = 2 là đường tiệm cận đứng
0,5
0,5
b/ Phương trình hoành độ giao điểm của (d) và (C) là: 
x(x2 + 3mx + 2 – m) = 0 
+ (d) cắt (C) tại ba điểm A, B, C(0; 1) khi và chỉ khi phương trình (1) có hai nghiệm phâm biệt khác 0 , suy ra (*)
+ Gọi A(xA; 1 – 3xA), B(xB; 1- 3yB), với xA + xB = - 3m ; xA.xB = 2 – m
0,25
0,25
0,5
0,25
3x0,25
3
a/ ; f(0) = -3; f(1) = - 2 ; f(2) = -11
2x0,5
0,5
b/ Ta có: 
Hàm số đạt cực đại tại x = 1 khi và chỉ khi 
2x0,25
2x0,5
ĐỀ 02
Câu
Nội dung
Điểm
1
a)
1. Tập xác định D = R
2. Sự biến thiên:
Chiếu biến thiên: 
Giới hạn: 
Bảng biến thiên:
x
 -2 0 2 
y’
	+	0	-	0	+	0	-
y
Kết luận các khoảng đồng biến, nghịch biến và cực trị của hàm số
3. Đồ thị 
0,25
3x0,25
0,25
0,75
0,25
0,75
b/ PT: có 4 nghiệm phân biệt khi đường thẳng (d): y = m - 1 cắt đồ thị (C) tại 4 điểm phân biệt, dựa vào đồ thị ta có: 
0,5
0,5
2
a/ ; y = 2 là đường tiệm cận ngang
 ; x = -2 là đường tiệm cận đứng
0,5
0,5
b/ Phương trình hoành độ giao điểm của (d) và (C) là: 
x(x2 + 3mx + 2 – m) = 0 
+ (d) cắt (C) tại ba điểm A, B, C(0; 1) khi và chỉ khi phương trình (1) có hai nghiệm phâm biệt khác 0 , suy ra (*)
+ Gọi A(xA; 1 – 3xA), B(xB; 1- 3yB), với xA + xB = - 3m ; xA.xB = 2 – m
0,25
0,25
0,5
0,25
3x0,25
3
a/ ; f(0) = 3; f(1) = 2 ; f(2) = 11
2x0,5
0,5
b/ 
Ta có: 
Hàm số đạt cực tiểu tại x = 1 khi và chỉ khi 
2x0,25
2x0,5