Đề kiểm tra học kì I Toán 12 (có đáp án)

Đề Kiểm Tra Học Kì I
Câu 1:
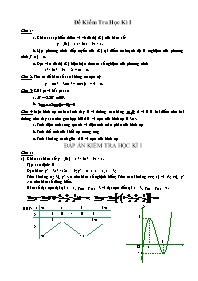
	a. Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số:
	y = f(x) = x3 - 6x2 + 9x - 1.
	b. Lập phương trình tiếp tuyến của (C) tại điểm có hoạnh độ là mghiệm của phương trình f”(x) = 0.
	c. Dựa vào đồ thị (C) biện luận theo m số nghiệm của phương trình
	x3 - 6x2 + 9x + 2 – m = 0.
Câu 2. Tìm m để hàm số sau không có cực trị:
	y = mx3 + 3mx2 – (m-1)x – 4 = 0.
Câu 3: Giải pt và bất pt sau
	a. .
	b. .
Câu 4: Một hình trụ có bán kính đáy R và đường cao bằng ; A và B là hai điểm trên hai đường tròn đáy sao cho góc hợp bởi AB và trục của hình trụ là 30o.
a. Tính diện tích xung quanh và diện tích toàn phần của hình trụ
b. Tính thể tích của khối trụ tương ứng
c. Tính khoảng cách giữa AB và trục của hình trụ
ĐÁP ÁN KIỂM TRA HỌC KÌ I
Câu 1:
Khảo sát hàm số: y = f(x) = x3 - 6x2 + 9x - 1.
Tập xác định: R
Đạo hàm: y’ = 3x2 - 12x + 9; y’ = 0 ó x = 1, x = 3;
Trên khoảng (1; 3), y’ 0 nên hàm số đồng biến.
Hàm số đạt cực đại tại x = 1, yCĐ = y(1) = 3 và đạt cực tiểu tại x = 3, yCT = y(3) = -1.
BBT: x -∞ 1 3 +∞ 
 y’ + 0 - 0 +
 3 +∞
 y 
 -∞ -1
 y
 3 
 3
 O 1 
 -1 
b) Ta có: f’(x) = 3x2 - 12x + 9; f”(x) = 6x - 12.
f”(x) = 0 6x - 12 = 0 x = 2 y = 1, f’(2) = -3.
Phương trình tiếp tuyến cần tìm là: y - 1 = -3(x - 2) y = -3x + 7.
c) Ta có:
x3 - 6x2 + 9x + 2 – m = 0 x3 - 6x2 + 9x - 1 = m -3
Số nghiệm của phương trình đã cho là số giao điểm của đồ thị (C) với đường thẳng y = m - 3. Dựa vào đồ thị (C) ta có:
 : Phương trình có một nghiệm.
 : Phương trình có hai nghiệm;
-1 < m - 3 < 3 2 < m < 6 : Phương trình có ba nghiệm.
Câu 2. Ta có: y = mx3 + 3mx2 – (m-1)x – 4 = 0 y’ = 3mx2 + 6mx - (m - 1).
Nếu 3m = 0 m = 0 thì y’ = 1 > 0. Hàm số không có cực trị.
Nếu 3m ≠ 0 thì y’ là một tam thức bậc hai. Hàm số không có cực trị khi và chỉ khi:
 .
Kết hợp lại ta có: thì hàm số không có cực trị.
Câu 3. 
a) Ta có: .
Đạt t = (t > 0), ta có bất phương trình đối với t là:
2t2 + t - 1 > 0 t > >x > ;
b) Ta có: ĐK: x > 0, x - 1 > 0 tức là x > 1.
Khi đó log2[x(x - 1)] = 1 x(x - 1) = 2 x2 - x - 2 =0 x = 2.
Câu 4.
Sxq = 2Rl = 2R = 2R2 (đvdt)
Stp = Sxq + 2Sđ = 2R2 + 2R2 = 2R2(+ 1) (đvdt).
V = Sđ.h = R2. = R3 (đvtt).