Đề kiểm tra học kì I môn : Toán lớp 12
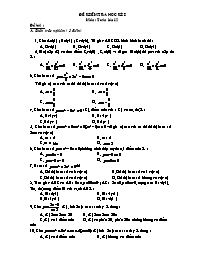
1. Cho A(2;1) ; B(2;-1) ; C(-2;-3). Tứ giác ABCD là hình bình hành thì :
A. D(-2;1) B. D(-2;-1) C. D(2;1) D. D(2;-1)
2. Một elíp (E) có tiêu điểm F1(-2;0) , F2(2;0) và đi qua M(2;3) thì ptct của elíp đó là :
A. x2 /16 + y2/12 = 1 B. x2 /16 + y2 / 9 = 1 C. x2 /16 + y2/4 = 1 D. x2/16 + y2/8 = 1
3. Cho hàm số y = x3/3 + 2x2 - 3mx + 5
Với giá trị nào của m thì đồ thị hàm số có 2 cực trị
A. m < 4/3="" b.="" m=""> 4/3
C. m = 4/3 D. m <>
4. Cho hàm số y = x3 - 3x2 + 6( C), điểm uốn của ( C ) có toạ độ là :
A. U(-1;-4) B. U( -1;4 )
C. U(1;-4 ) D. U(1;4 )
Bạn đang xem tài liệu "Đề kiểm tra học kì I môn : Toán lớp 12", để tải tài liệu gốc về máy bạn click vào nút DOWNLOAD ở trên
ĐỀ KIỂM TRA HỌC KÌ I Môn : Toán lớp 12 Đề bài : A. Phần trắc nghiệm ( 3 điểm) 1. Cho A(2;1) ; B(2;-1) ; C(-2;-3). Tứ giác ABCD là hình bình hành thì : A. D(-2;1) B. D(-2;-1) C. D(2;1) D. D(2;-1) 2. Một elíp (E) có tiêu điểm F1(-2;0) , F2(2;0) và đi qua M(2;3) thì ptct của elíp đó là : A. B. C. D. 3. Cho hàm số Với giá trị nào của m thì đồ thị hàm số có 2 cực trị A. B. C. D. 4. Cho hàm số ( C), điểm uốn của ( C ) có toạ độ là : A. U(-1;-4) B. U( -1;4 ) C. U(1;-4 ) D. U(1;4 ) 5. Cho hàm số với giá trị nào của m thì đồ thị hàm số luôn có cực trị A. m 2 C. m = D. 6. Cho hàm số phương trình tiếp tuyến tại điểm uốn là : A. B. C. D. 7. Hàm số thì A. Đồ thị hàm số có 3 cực trị B. Đồ thị hàm số có 1 cực trị C. Đồ thị hàm số có 2 cực trị D. Đồ thị hàm số không có cực trị 8. Tam giác ABC có AB: ; AC : , trọng tâm G( -2;-1). Toạ độ trung điểm M của cạnh AB là : A. M( 2;-1) B. M( -1;-2 ) B. M( 1;-2 ) D. M( -2;1 ) 9. Cho (C) , kết luận nào sau đây là đúng : A. (C) luôn luôn lồi B. (C) luôn luôn lõm C. (C) có 1 điểm uốn D. (C) có phần lồi, phần lõm nhưng không có điểm uốn 10. Cho (C) kết luận nào sau đây là đúng : A. (C) có 2 điểm uốn B. (C) không có điểm uốn C. (C) có 1 điểm uốn D. (C) có 2 tiệm cận 11. Cho A( -2; 5 ) , B( 2;3) đường thẳng (d) : x - 4y + 4 = 0 cắt đoạn AB tại M, toạ độ của điểm M là : A. M( 4;-2 ) B. M( -4;2 ) C. M( 4;2 ) D. M( 2;4 ) 12. Tam giác ABC có A( -1;-3 ) đường cao BB ’ : 5x + 3y -25 = 0 , CC ’ : 3x + 8y -12 = 0, toạ độ đỉnh B là : A. B( 5;2 ) B. B( 2;5 ) C. B( 5;-2 ) D. B( 2;-5 ) B. Phần tự luận ( 7 điểm) Câu 1 : a. Khảo sát hàm số ; ( C) b. Từ đồ thị ( C ) xác định m để phương trình có hai nghiệm phân biệt x1, x2 thoả mãn x1< 2 < x2 Câu 2 : Cho hàm số ; Đồ thị ( H ) CMR : Không có tiếp tuyến nào của ( H ) đi qua giao điểm 2 tiệm cận của ( H ) Câu 3 : Trong hệ toạ độ Oxy cho 3 điểm A(-1;2) ; B(2;1) ; C(2;5) a. Viết phương trình các đường trung trực của b. Xác định phương trình đường tròn ngoại tiếp ĐÁP ÁN A. Phần trắc nghiệm : 1. B ( 0,25đ) 2. A ( 0,25đ) 3. D ( 0,25đ) 4. D ( 0,25đ) 5. C ( 0,25đ) 6. B ( 0,25đ) 7. B ( 0,25đ) 8. B ( 0,25đ) 9. D ( 0,25đ) 10. C ( 0,25đ) 11. C ( 0,25đ) 12. B ( 0,25đ) B. Phần tự luận : Giải Điểm Txđ D=R\ 0,25đ 0,25đ + HS ĐB trên các khoảng : (-h;0) và ( 2;+h) + HS NB trên các khoảng ( 0;1) và ( 1;2) 0,25đ + Điểm CĐ : ( 0;2) + Điểm CT : (2;2) 0,25đ + Giới hạn + Tiệm cận: + đường thẳng x = 1 là tiệm cận đứng . đường thẳng y = x – 1 là tiệm cận xiên . 0,5đ Bbt x 0 1 2 y’ + 0 - - 0 + y -2 CĐ 2 CT bảng giá trị đặc biệt . x -1 0 1 2 3 y -2 2 0,5đ Nhận xét đồ thị : Đồ thị có 1 tâm đối xứng là giao điểm của 2 đường tiệm cận 0,5đ 2. Pt(1) , từ đồ thị pt(1) có 2 nghiệm : x1< 2 < x2 với m>2 0,25đ 0,25đ 3. Xét tiếp tuyến bất kỳ của (H) tại M0(x0;f(x0)) pt của tiếp tuyến là : Giao điểm của 2 đường tiệm cận là I( 1;2 ) Tiếp tuyến này đi qua I nếu vô lí vậy không có tiếp tuyến nào của (H) đi qua điểm uốn của 2 tiệm cận 0,25đ 0,25đ II.1> Gọi P,Q ,R là trung điểm của AB, BC, AC . ta có : Gọi d1; d2; d3 là các trung trực qua P; Q; R. Ta có : d1 nhận là vtpt. tương tự: 0,5đ 0,25đ 0,25đ 0,5đ 0,5đ 2>Gọi I(x;y) là tâm đường tròn ngọai tiếp tam giác ABC. Ta có : I = d2 d3 0,5đ Và bán kính : 0,25đ Vạy phương trình của đường tròn là : (x – 1)2 + (y – 3)2 = 5 0,25đ
Tài liệu đính kèm:
 0607_Toan12_hk1_TLAK.doc
0607_Toan12_hk1_TLAK.doc





