Đề kiểm tra 45 phút môn Toán 12, phần giải tích

BÀI KIỂM TRA 45 PHÚT
Tiết: 21
Ngày soạn: 
A. Mục tiêu:
	+) Kiến thức
Ứng dụng đạo hàm, Sơ đồ khảo sát hàm số.
+) Kĩ năng:
Biết khảo sát một số hàm đơn giản.
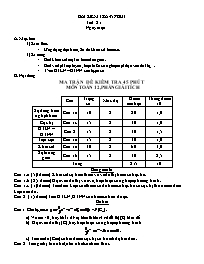
Biết viết pt tiếp tuyến, biện luËn số nghiệm pt dựa vào đồ thị, 
T×m GTLN – GTNN cña hµm sè
B. Nội dung
MA TRẬN ĐỀ KIỂM TRA 45 PHÚT
 MÔN TOÁN 12, PHẦN GIẢI TÍCH
Câu
Trọng số
Mức độ
Điểm
 ma trận
Thang điểm 10
Sự đồng biến
nghịch biến 
Câu 1a
10
2
20
1,0
Cực trị
Câu 1c
15
2
30
1,0
GTLN – GTNN
Câu 2
15
2
30
1,5
Tiện cận
Câu 1a
15
2
30
1,0
Khảo sát
Câu 1a
30
2
60
3,0
Sự tương giao
Câu 1b
15
2
30
2,5
Tổng
215
10
Bảng mô tả
Câu 1.a: (5,0 điểm) Khảo sát sự biến thiên và vẽ đồ thị hàm số bậc ba.
Câu 1.b: (2,5 điểm) Dựa vào đồ thị vừa vẽ, biện luận số nghiệm phương trình.
Câu 1.c: (1,0 điểm) Tìm điều kiện của tham số để hàm số bậc ba có cực trị thỏa mãn điều kiện nào đó.
Câu 2: (1,5 điểm) Tìm GTLN, GTNN của hàm số trên đoạn.
Đề bài
Câu 1: Cho hµm sè (Cm).
	a) Với m = 0, hãy kh¶o s¸t sự biến thiên vµ vÏ ®å thÞ (C) hµm sè. 
	b) Dựa vào đồ thị (C), hãy biện luận số nghiệm phương trình 
.
	c) Tìm m để (Cm) có hai điểm cực trị có hoành độ trái dấu.
Câu 2: Tìm giá trị lớn nhất, nhỏ nhất của biểu thức
	 trên [1; 3]
Hướng dẫn
a) Kh¶o s¸t sự biến thiên vµ vÏ ®å thÞ hµm sè (C)
+) TXĐ: D = R.
+) Sự biến thiên
	- Có y’ = - x2 – 2x + 3. y’ = 0 ó -x2 – 2x + 3 = 0 ó x = 1; x = -3.
	- 
	- Bảng biến thiên: 
x
- ∞
-3 1
+ ∞
y’
- 0 + 0 -
y
-12
-4/3
+ ∞
- ∞
Hàm số đạt cực đại tại x = -3 và yCĐ = -12. đạt cực tiểu tại x = 1 và yCT = -4/3.
Hàm số đồng biến (-3; 1), nghịch biến trên (- ∞; -3) và (1; + ∞).
+) Đồ thị hàm số
b) Dựa vào đồ thị (C), hãy biện luận số nghiệm phương trình 
 (1)
Ta có: (1) . Khi đó số nghệm của phương trình (1) bằng số giao điểm của đồ thị (C) và đường thẳng d: y = m -3. Suy ra
Nếu thì (C) cắt d tại một điểm hay phương trình (1) có một nghiệm.
Nếu thì (C) cắt d tại hai điểm hay phương trình (1) có hai nghiệm phân biệt.
Nếu thì (C) cắt d tại ba điểm hay phương trình (1) có ba nghiệm phân biệt.
c) Tìm m để (Cm) có hai điểm cực trị có hoành độ trái dấu.
- Ta có , Để đồ thị hàm số có hai điểm cực trị có hoành độ trái dấu ↔ y’ = 0 có hai nghiệm trái dấu ↔a.c -1.
	Vậy m < -1 thỏa mãn bài toán.
Câu 2: Tìm giá trị lớn nhất, nhỏ nhất của biểu thức
	 trên [1; 3]
Lời giải:
	- Ta có: f’(x) = 
Có f(1) = 4, f(2) = 3, f(3) = 10/3.
- Vậy