Đề kiểm tra 15 phút tiết 9: Hình học 12 (theo chương trình chuẩn)

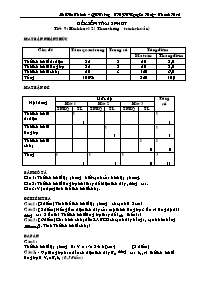
Đề kiểm tra 15 phút
Tiết 9: Hình học 12 ( Theo chương trình chuẩn)
Ma trận nhận thức
Chủ đề
Tầm quan trọng
Trọng số
Tổng điểm
Ma trận
Thang điểm
Thể tích khối đa diện
25
2
50
2,0
Thể tích khối lăng trụ
25
2
50
2,0
Thể tích khối chóp
50
3
150
6,0
Tổng 
100%
250
10,0
Ma trận đề
Nội dung
Mức độ
Tổng số
Mức 1
Mức 2
Mức 3
TNKQ
TL
TNKQ
TL
TNKQ
TL
Thể tích khối đa diện
1
 2
1
 2
Thể tích khối lăng trụ
1
	2	2
1
 2
Thể tích khối chóp
1
	 6
1
 6
Tổng 
1
	 2
1
	 2
1
	 6
3
 10
Bản mô tả
Câu 1: Thể tích khối lập phương biết cạnh của hình lập phương.
Câu 2: Thể tích khối lăng trụ khi thay đổi diện tích đáy, đường cao.
Câu 3: Vận dụng tính thể tích khối chóp.
Đề kiểm tra
Câu 1: (2 điểm) Tính thể tích khối lập phương có cạnh là 2 cm? 
Câu 2: ( 2 điểm) Nếu giảm diện tích đáy của một hình lăng trụ 3 lần và tăng độ dài đường cao 2 lần thì Thể tích khối lăng trụ thay đổi như thế nào?
Câu 3: ( 6 điểm) Cho hình chóp đều S.ABCD có cạnh đáy bằng a, cạnh bên bằng . Tính Thể tích khối chóp?
Đáp án
Câu 1: 
Thể tích khối lập phương là: V = a3 = 23= 8 (cm3)	( 2 điểm)
Câu 2: - Gọi lăng trụ ban đầu có diện tích đáy B1, đường cao h1, và thể tích khối lăng trụ là V1= B1h1 ( 0,5 điểm)
- Lăng trụ sau có diện tích đáy , đường cao , do đó thể tích khối lăng trụ là: 	 ( 1 điểm)
- Vậy thể tích khối lăng trụ sau bằng 2/3 thể tích khối lăng trụ ban đầu. ( 0,5 điểm)
S
Câu 3: 
C
D
O
B
A
- Khối chóp tứ giác đều nên đáy là hình vuông cạnh a có diện tích đáy B = a2(đvdt) Gọi O là tâm hình vuông thì , đồng thời SO là đường cao của khối chóp. ( 2 đ)
Ta có: SOA là tam giác vuông đỉnh O nên : (đvd) ( 2đ)
Do đó thể tích khối chóp là: (đvtt). ( 2 đ)
Vậy khối chóp S.ABCD có thể tích là: (đvtt).	
-------------- Hết ----------------
Đề kiểm tra 15 phút
Tiết 32: Hình học 12 ( Theo chương trình chuẩn)
Ma trận nhận thức
Chủ đề
Tầm quan trọng
Trọng số
Tổng điểm
Ma trận
Thang điểm
Véc tơ pháp tuyến của mặt phẳng
25
1
25
1,0
Phương trình tổng quát của mặt phẳng
40
3
120
5,0
Điều kiện để 2 mặt phẳng song song
15
3
45
2,0
Khoảng cách từ một điểm đến mặt phẳng
20
2
40
2,0
Tổng 
100%
230
10,0
Bản mô tả
Câu 1: Nhận biết véc tơ pháp tuyến của mặt phẳng có phương trình cho trước.
Câu 2: Lập phương trình mặt phẳng đi qua một điểm và song song với một mặt phẳng cho trước.
Câu 3: Tính khoảng cách từ một điểm đến một mặt phẳng
Đề kiểm tra
Trong hệ toạ độ Oxyz cho điểm A(1;2;5) và mp ( P) : 2x – y +2z – 4 = 0
Tìm một véc tơ pháp tuyến của mp(P).
Lập phương trình mp(Q) đi qua A và song song với mp (P).
Tính khoảng cách từ A đến mặt phẳng (P).
Đáp án:
Mặt phẳng (P) có một véc tơ chỉ phương là: 	(1,0 đ)
Mặt phẳng (Q) đi qua điểm A(1;2;5) và song song với mặt phẳng (P) nên nhận véc tơ làm một véc tơ pháp tuyến.	(2,0 đ)
 Do đó, có phương trình tổng quát: 
2( x-1) – ( y- 2) + 2 (z- 5) = 0
	(5,0 đ)
Khoảng cách từ điểm A đến mặt phẳng (P) là:
	(2,0 đ)
------------------------------------Hết--------------------------------