Chuyên đề về Bất đẳng thức môn Toán 12
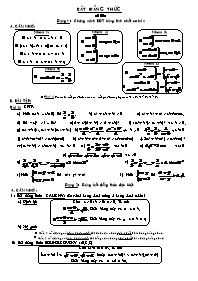
Dạng 1: Chứng minh BĐT bằng tính chất cơ bản
? Chú ý: Từ các kết quả trên, suy ra kết quả tương tự cho A < b;="" a="" b;="" a="">
B. BÀI TẬP:
Bài 1: CMR
Dạng 2: Dùng bất đẳng thức đặc biệt
A. CẦN NHỚ:
1/ Bất đẳng thức CAUCHY: (So sánh trung bình cộng & trung bình nhân)
Bạn đang xem tài liệu "Chuyên đề về Bất đẳng thức môn Toán 12", để tải tài liệu gốc về máy bạn click vào nút DOWNLOAD ở trên
BẤT ĐẲNG THỨC o000o Dạng 1: Chứng minh BĐT bằng tính chất cơ bản Nhóm 3: ¯ ¯ Nhóm 2: ¯ ¯ Nhóm 1: ¯ a > b Û a – b > 0 ¯ [(a > b)Ù(b > c)] Þ (a > c) ¯ a > b + c Û a - c > b ¯ a > b Û a + c > b + c. A. CẦN NHỚ: Nhóm 5: ¯ ¯ Nhóm 4: ¯ ¯ Chú ý: Từ các kết quả trên, suy ra kết quả tương tự cho A < B; A ³ B; A £ B. B. BÀI TẬP: Bài 1: CMR Nếu (a>b Ù ab>0) thì . b) a2 + ab + b2 ³ 0 c) a2 + b2 + c2 ³ ab+bc+ca. 2(1 - a)2 ³ 1 – 2a2 e) (1+ a2)(1+ b2) ³ (1 + ab)2 f) 4(a3+ b3)³ (a + b)3 "a, b ³ 0. g) (a3 + b3)2£ (a2 + b2)(a4 + b4) h)"a, b ³ 0 i) "a,b>0 j) a2+b2+c2+d2 ³ (a+b)(c+d) k) a2+ b2+ c2+ d2+ e2 ³ a(b+c+d+e) l) 3(a2+ b2+c2) ³ (a+b+c)2 m) (a3+ b3) ³ ab(a+ b) "a, b³ 0 n) "a>b>0 o) "a>2 p) "a ³0 q) r) s) Nếu thì x3 > y3 + z3 t) Nếu thì . Dạng 2: Dùng bất đẳng thức đặc biệt A. CẦN NHỚ: 1/ Bất đẳng thức CAUCHY: (So sánh trung bình cộng & trung bình nhân) a) Định lý: Cho a ³ 0; b ³ 0; c ³ 0. Ta có: ¯. Dấu bằng xảy ra Û a = b. ¯. Dấu bằng xảy ra Û a = b = c. b) Hệ quả: ¯ Nếu 2 số dương có tổng không đổi thì tích của chúng lớn nhất khi chúng bằng nhau. ¯ Nếu 2 số dương có tích không đổi thì tổng của chúng nhỏ nhất khi chúng bằng nhau. 2/ Bất đẳng thức BOUNIACOVSKY: (B.C.S) Cho a; b; c; dỴR. Ta có: ïac + bdï £ hoặc (ac + bd)2 £ (a2+ b2).(c2+ d2) Dấu bằng xảy ra Û ad = bc. 3/ Bất đẳng thức TRỊ TUYỆT ĐỐI: Cho a, bỴR. Ta có: ¯ - ïạ £ a £ ïạ ¯ơơaơ-ơbơơ £ ơa + bơ ơaơ+ïbï. Dấu bằng xảy ra Û ab ³ 0. 4/ Bất đẳng thức TAM GIÁC: Cho a, b, c là 3 cạnh tam giác. Ta có: ơơbơ-ơcơơ< a <ơbơ+ïcï. BÀI TẬP: Bài 2: CMR a) ; "a,b ¹ 0. b) "a,bỴR. Bài 3: CMR a) b) (a+b)(ab+4)³ 8ab "a,b ³ 0 c) a + b + 1 ³ d) £ ab "a,b ³ 1 e) "a,b,c,d ³ 0. f) Nếu a; b; c ³ 0; a+b+c=1 thì (1-a)(1–b)(1–c)³8abc. Bài 4: CMR a) b) c) x2 + Bài 5: CMR a)ï15sinx + 8cosxï£ 17 b) Nếu a + b ³ 1 thì 2a2 + 2b2 ³ 1 c) Nếu a; b ³ c ³ 0 thì d) Nếu 4x - y = 1 thì x2 + y2 ³; 4x2 + y2 ³. Bài 6: Cho DABC có 3 cạnh a, b, c - p là nửa chu vi - S là diện tích. CMR: a) p > a; p > b; p > c. b) abc ³ (a + b – c)(b+ c – a)(c + a – b). c) a2 + b2 + c2 < 2(ab + bc + ca). d) a4 + b4 + c4 ³ 16S2. Trong các bất đẳng thức trên, dấu bằng xảy ra khi nào ? Bài 7: Tìm gtnn của các hàm số sau đây: a) y = f(x) = b) ; "x>1 c) y = f(x) = d) y= f(x)= e) ; "x>0 Bài 8: Tìm gtln của các hàm số sau đây: a) y = f(x) = x(3 – x) "xỴ[0; 3] b) y = f(x)= x(8 – 2x) "xỴ[0; 4] c) y = f(x) = d) y = f(x) = sin2x.cosx "xỴ[0o; 90o] Bài 9: Tìm gtln & gtnn của hàm số: y = f(x) = "xỴ[1; 4]. Bài 10: a) Tìm hcn có chu vi lớn nhất & nội tiếp trong nửa đường tròn tâm O, bán kính R cho trước. b) Người ta cắt bỏ 4 hình vuông nhỏ bằng nhau ở 4 góc 1 tấm bìa hình vuông cạnh a để làm 1 cái hộp không nắp. Tính cạnh hình vuông nhỏ để hộp có thể tích V lớn nhất ? c) Cho DABC đều cạnh a. Người ta dựng 1 hình chữ nhật MNPQ có cạnh MN nằm trên cạnh BC & 2 đỉnh P, Q theo thứ tự nằm trên 2 cạnh AC & AB. Xác định vị trí điểm M sao cho dt(MNPQ) lớn nhất ? Tính gtln đó. Gv: Đỗ Khánh Giang
Tài liệu đính kèm:
 BDT.doc
BDT.doc





