Chuyên đề: Nguyên hàm và tính tích phân

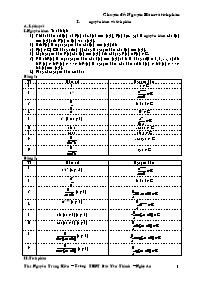
nguyên hàm và tích phân
A. Lý thuyết
I. Nguyên hàm. Ta nhớ lại:
Với hai hàm số f(x) và F(x) xác định trên (a;b), F(x) được gọi là nguyên hàm của f(x) trên (a;b) nếu F’(x) = f(x) "x ẻ (a;b).
Nếu F(x) là một nguyên hàm của f(x) trên (a;b) thì:
F(x) + C ( C là hằng số tuỳ ý) cũng là nguyên hàm của f(x) trên (a;b).
Mọi nguyên hàm G(x) của f(x) trên (a;b) đều có dạng G(x) = F(x) + C.
Giả sử Fi(x) là một nguyên hàm của fi(x) trên (a;b) và ki là hằng số (i = 1, 2, , n) thì: k1F1(x) + k2F2(x) +  + knFn(x) là nguyên hàm của hàm số k1f1(x) + k2f2(x) +  + knfn(x) trên (a;b).
Bảng các nguyên hàm cơ bản:
Bảng 1:
TT
Hàm số
Nguyên hàm
1
1
x + C
2
xa
3
ln | x | + C
4
ex
Ex + C
5
ax (0 < a ≠ 1)
6
sin x
- cos x + C
7
cos x
sin x + C
8
- cotg x + C
9
tg x + C
Bảng 2:
TT
Hàm số
Nguyên hàm
1
uau’ (a ≠ -1)
2
ln | u | + C
3
 (a ≠ 0)
4
eax + b (a ≠ 0)
5
sin (ax + b) (a ≠ 0)
 C
6
cos (ax + b) (a ≠ 0)
7
 (a ≠ 0)
8
 (a ≠ 0)
II. Tích phân
Cho hàm số f(x) liên tục trên [a;b], F(x) là một nguyên hàm của f(x) trên [a;b]. Tích phâ từ a đến b của f(x) là: = F(b) - F(a).
Để tính tích phân quy về tìm một nguyên hàm F(x) của f(x) trên [a;b]. Tuy nhiên việc tìm trực tiếp nguyên hàm ấy gặp khps khăn, cần biết them các phương pháp sau để tính tích phân:
1) Phương pháp tích phân tứng phần:
Giả sử u(x), v(x) có đạo hàm liên tục trên [a;b], ta có:
 hay .
Để tính bằng phương pháp này ta xem f(x)dx có dạng udv, sau đó tìm u, v và áp dụng công thức trên.
2) Phương pháp đổi biến số
Giả sử: a) x = j(t) có đạo hàm liên tục trên [a;b]
	b) j(a) = a; j(b) = b,
	c) t ẻ [a;b] Û x ẻ [a;b].
Thế thì: .
Thực chất của công thức này chỉ là thay x bởi j(t), thay dx bởi j’(t)dt, sau đó thay các cận tương ứng của tích phân.
III. ứng dụng của tích phân vào việc tính diện tích và thể tích
1) Tính diện tích:
Cho hai hàm số f(x) và g(x) liên tục trên [a;b]. Diện tích hình phẳng bị chắn bởi đồ thị hàmsố y = f(x), y = g(x) và các đường thẳng x = a, x = b được xác định bởi công thức:
.
Nếu f(x) ≥ g(x) " x ẻ [a;b] thì .
Diện tích hình phẳng giới hạn bởi đồ thị x = f(y), x = g(y) liên tục trên [c;d] và các đường thẳng y = c, y = d là: .
2) Tính thể tích khối tròn xoay
Cho hàm số f(x) liên tục trên [a;b]. Hình phẳng giới hạn bởi các đường y = f(x), y = g(x), x = a, x = b, khi quay xung quqnh trục Ox gây nên một khối tròn xoay, có thể tích xác địng bởi:
.
Hình phẳng giới hạn bởi đồ thị hàm số x = g(y) liên tục trên [c;d], các đường thẳng x = 0, x = c, x = d, khi quay xung quanh trục Oy gây nên một khối tròn xoay có thể tích là: .
B. Các dạng bài tập
1. Các nguyên hàm và tích phân đơn giản
Trong nhiều trường hợp để tìm nguyên hàm và tính tích phân ta chỉ việc áp dụng các tình chất của chúng và bảng các nguyên hàm cơ bản. Sau đây là một số ví dụ.
Ví dụ 1. Tìm nguyên hàm các hàm số sau:
1) ;	2) 2x32x53x;	3) ;
4) ;	5) e3 cosxsinx;	6) tg2x;
7) x cos x2;	8) ;	9) ;
10) ;	11) ;	12) (2x - 3)(x2 - 3x + 1)10.
HD. 1) f(x) = ị F(x) = + C.
2) f(x) = (2.32.53)x ị F(x) = + C.
3) f(x) = (x > 0), f(x) = (x < 0) ị F(x) = + C.
4) .
5) f(x)dx = , với u = 3cosx ị F(x) = .
6) f(x) = ị F(x) = tg x - x + C.
7) f(x)dx = , với u = x2 ị F(x) = .
8) f(x)dx = , với u = sinx ị F(x) = .
9) f(x)dx = , với u = (ax2 + b) ị F(x) = .
10) f(x)dx = , với u = 2ln x + 3 ị F(x) = .
11) f(x)dx = , với u = 5x2 + 3 ị F(x) = .
12) f(x)dx = u10du, với u = x2 - 3x + 1 ị F(x) = .
Ví dụ 2. Tính các tích phân sau:
1) ;	2) ;	3) ;
4) ;	5) dx;	6) ;
7) ;	8) ;	9) ;
10) ;	11) ;	12) .
HD. 1) Đặt , đưa về tính tích phân: . 
2) Đặt , đưa về tính tích phân: .
3) sinx cos3x = sinx cosx (1 + cos2x - 1). Đặt 1 + cos2x = t ị -2 sinx cosx dx = dt, đưa về tính tích phân: .
4) Đặt ị 3dx = 2t dt, đưa về tính tích phân: = = .
5) Đặt ị dx = -2t dt, đưa về tính tích phân: .
6) Nếu a2 ≠ b2: Đặt a2sin2x + b2cos2x = t ị 2(a2 - b2)sinx cosx dx = dt. Đưa về tính tích phân: .
Nếu a2 = b2: đưa về tính tích phân: .
7) Đưa về tính: .
8) . Đặt , đưa về tính tích phân:
.
10) = 2ln3 - 3ln2.
11) = .
12) Đặt ln(lnx) = t ị , đưa về tính: .
2. Nguyên hàm và tích phân các phân thức hữu tỉ
Các phân thức hữu tỉ có dạng , trong đó P(x), Q(x) là các đa thức.
Để tìm nguyên hàm của phân thức này trước hết ta hãy xem bậc của P(x) và Q(x). Nếu bậc P(x) lớn hơn bậc Q(x), khi đó ta thực hiện phép chia P(x) cho Q(x) để được thương A(x) và dư R(x), tức là , với bậc R(x) < bậc Q(x).
Việc tìm nguyên hàm của đa thức A(x) không có gì khó khăn. Bài toán qui về tìm nguyên hàm của phân thức , trong đó bậc R(x) < bậc Q(x).
Ta xét các trường hợp sau của Q(x):
1) Q(x) là đa thức bậc nhất: Q(x) = ax + b ị R(x) là một hằng số, ta có:
.
Ngoài ra ta còn có: (m ≠ 1).
2) Q(x) là đa thức bậc hai, tức .
KN1. Nếu Q(x) có 2 nghiệm phân biệt x1, x2:
Khi đó hãy tìm các hằng số A, B sao cho: .
Việc tìm nguyên hàm đã cho đưa về tìm nguyên hàm các phân thức hữu tỉ có mẫu thức bậc nhất.
KN2. Q(x) có nghiệm kép x = x0:
Khi đó hãy tìm các hằng số A, B sao cho: .
KN3. Q(x) vô nghiệm (trường hợp này chỉ gặp trong bài toán tính tích phân):
Trong trường hợp này ax2 + bx + c có dạng a[(x + p)2 + q2], do đó hãy đặt x + p = q tgt để suy ra kết quả.
3) Q(x) là đa thức bậc 3: Chỉ có các khả năng sau của Q(x)
KN1. Q(x) có 3 nghiệm phân biệt x1, x2, x3, tức là: Q(x) = a(x - x1)(x - x2)(x - x3)
Khi đó hãy tìm các hằng số A, B, D sao cho: .
KN2. Q(x) có nghiệm kép x1 và nghiệm đơn x2, tức là: Q(x) = a(x - x1)2(x - x2)
Khi đó hãy tìm các hằng số A, B, D sao cho: .
KN3. Q(x) có dạng a(x - x0)3:
Khi đó hãy tìm các hằng số A, B, D sao cho: .
KN4. Q(x) chỉ có 1 nghiệm đơn x1, tức là Q(x) = (x - x1)(ax2 + bx + c)
Khi đó hãy tìm các hằng số A, B, D sao cho: .
4) Q(x) là đa thức có bậc lớn hơn 3: Trường hợp này chỉ xét các nguyên hàm hoặc tích phân “Đặc biệt”
Tuy nhiên nếu Q(x) có bậc n và giả sử ta tìm được một nghiệm của nó là x = x1 thì có dạng: , trong đó Qn - 1(x) là đa thức bậc n - 1, R’(x) có bậc < n - 1. 
Việc tìm nguyên hàm của diễn ra theo quá trình trên.
Chú ý. Để tìm các hằng số bất định A, B, D, ta quy đồng mẫu số, so sánh các hệ số của cùng một luỹ thừa của x ở vế trái và vế phải của đồng nhất thức thu được và giải hệ phương trình đối với các hệ số cần tìm. Có thể xác định các hệ số này bằng cách khác là cho biến x trong đồng nhất thức những trị số tuỳ ý. Dùng kết hợp cả hai phương pháp thường là có lợi.
Ví dụ 1. Tìm nguyên hàm của các hàm số:
1) ;	2) ;	3) ;
4) ;	5) ;	6) ;	7) .
Giải. 1) Nếu a = b: nguyên hàm là + C.
Nếu a ≠ b: Vì nên . Do đó nguyên hàm là: .
2) Vì x2 - 4 = (x - 2)(x + 2), nên ta tìm hai số A, B sao cho: (*).
Quy đồng mẫu số (*) ta được x + 1 = A(x + 2) + B(x - 2). Trong đồng nhất thức này, cho x = 2, ta tìm được , cho x = -2 ta tìm được .
Từ đó tìm được nguyên hàm hàm số đã cho là: .
3) Vì x2 - 3x + 2 = (x - 1)(x - 2) nên . Do đó nguyên hàm là:
.
4) Chia tử thức cho mẫu thức, ta được: .
Để tìm nguyên hàm của , ta phân tích . Quy đồng mẫu thức ta được: 4x - 1 = A(x - 2) + B(x - 1). Cho x = 1 ị A = -3, cho x = 2 ị B = 7.
Vậy . Từ đó tìm được nguyên hàm là 
5) x2 - 2x + 1 có nghiệm kép x = 1, nên ta phân tích . Quy đồng mẫu thức ta được: x + 4 = A + B(x - 1) ị A = 5, B = 1. Từ đó suy ra nguyên hàm là: 
.
Chý ý. Có thể thấy ngay x + 4 = (x - 1) + 5 suy ra cách phân tích như trên.
6) Chia tử thức cho mẫu thức ta được:
 = x + 2 + .
Từ đó tìm được nguyên hàm là: .
Chú ý. Có thể phân tích: x3 = A(x - 1)3 + B(x - 1)2 + D(x - 1) + E ị A = 1, B = 3, D = 3, E = 5
Do đó: .
7) Vì x3 - 1 = (x - 1)(x2 + x + 1) nên ta phân tích:
. Quy đồng mẫu thức ta được
x + 1 = A(x2 + x + 1) + (Bx + D)(x - 1). Cho x = 1 ta tìm được . So sánh luỹ thừa của x2 hai vế ta suy ra: A + B = 0 ị . Cho x = 0 ta tìm được 1 = A - D ị .
Vậy . Từ đó tìm được nguyên hàm là: 
 + C.
Ví dụ 2. Tính các tích phân sau:
1) (a > 0);	2) ;	3) ;
4) ;	5) .
Giải. 1) Đặt x = a tgt, ị dx = a(1 + tg2t)dt; x2 + a2 = a2(1 + tg2t). Ta có:
.
2) . Đặt x + 3 = 4tgt, ị dx = 4(1 + tg2t)dt. Đưa về tính tích phân: .
3) Ta có: = =
= = .
Đặt , . Đưa về tính tích phân .
4) Chia tử thức cho mẫu thức a được:
. Từ đó ta có:
 = = 
 + = = .
5) Ta phân tích. Quy đồng mẫu thức ta được:
1 = A(x2 - x + 1) + (Bx+D)(x + 1)
Cho x = -1 ị , so sánh hệ số của x2 ở hai vế suy ra 0 = A + B ị . Cho x = 0 ta được: 1 = A + D ị .
Từ đó suy ra: = = 
= = .
Đặt ị .
Vậy: .
Ví dụ 3. Tính các nguyên hàm và tích phân sau:
1) ;	2) ;	3) ;
4) ;	5) ;	6) ;
7) ;	8) ;	9). .
Giải. 1) Ta tìm các số A, B, D sao cho:
.
Khử mẫu số:
x2 + 2x + 6 = A(x - 2)(x - 4) + B(x - 1)(x - 4) + D(x - 1)(x - 2)
Cho x = 1 ị 9 = 3A ị A = 3.
Cho x = 2 ị 14 = -2B ị B = -7.
Cho x = 4 ị 30 = 6D ị D = 5.
Vậy: = 
3 ln | x - 1 | - 7 ln | x - 2 | + 5 ln | x - 4 | + C.
2) Phân tích: 
Khử mẫu số: x2 + 1 = A(x +3) + B(x - 1)(x + 3) + D(x - 1)2(x + 3) + E(x - 1)3.
Cho x = 1 ị 2 = 4A ị .
Cho x = -3 ị 10 = -64E ị .
So sánh luỹ thừa cao nhất (tức x3) ở hai vế ị 0 = D+ E ị .
Cho x = 0 ị 1 = 3A - 3B + 3D - E ị .
Vậy: = = 
= .
3) Phân tích mẫu số thành nhân tử: x5 - x2 = x2(x - 1)(x2 + x + 1). Khi đó:
.
Khử mẫu số: 1 = A(x - 1)(x2 + x + 1) + Bx(x - 1)(x2 + x + 1) + Dx2(x2 + x + 1) + (Ex + F)(x - 1)x2
Cho x = 0 ị 1 = -A ị A = -1.
Cho x = 1 ị 1 = 3D ị .
So sánh các hệ số của x4, x3, x2 ta được hệ PT:
 ị .
Vậy: = = 
= = 
= = .
4) Ta phân tích: 
Khử mẫu: x3 - 2x = Ax + B + (Dx + E)(x2 + 1)
So sánh hệ số x3: 1 = D ị D = 1.
So sánh hệ số x2: 0 = E ị E = 0.
So sánh hệ số x: -2 = A + D ị A = -3.
So sánh hệ số tự do (cho x = 0): 0 = B + E ị B = 0.
Vậy: = = = 
= .
5) Tách phần nguyên: .
Bây giờ ta phân tích: .
Khử mẫu: 8x3 - 16x + 1 = A(x + 2)2 + B(x - 2)(x + 2)2 + D(x - 2)2 + E(x - 2)2(x + 2)
Cho x = 2 ị 33 = 16A ị .
Cho x = -2 ị -31 = 16D ị .
Cho x = 0 ị 1 = 4A - 8B + 4D + 8E ị ; 
So sánh hệ số x3: 8 = B + E.
Từ đó: .
Vậy: = = 
= .
6) Ta phân tích: 
Khử mẫu: x + 1 = (Ax + B)(x2 + 9) + (Dx + E)(x2 + 1).
So sánh hệ số của x3, x2, x, x0:
 Û .
Vậy: = 
= = .
7) = = 
= = .
Để tính ta đặt x + 1 = 3 tgt, , đưa về tính tích phân .
Vậy: .
8) Ta có: x4 + 1 = (x2 + 1)2 - 2x2 = . Do đó ta phân tích:
.
Khử nẫu: 
So sánh các hệ số x3, x2, x, x0 suy ra:
 Û .
Vậy: = 
= = .
Nhận xét: Để tính tích phân dạng , trong đó đoạn [a;b] không chứa điểm 0, ta có thể làm như sau:
 = 
Đặt , đưa về tính tích phân: .
9) = 
= = = .
Bài tập:
1. Tính các nguyên hàm và tích phân sau:
1) ;	2) ;	3) ;
4) ;	5) ;	6) ;
7) ;	8);	9) .
2. Tính các nguyên hàm và tích phân sau:
1) ;	2) ;	3) ;
4) ;	5) ;	6) ;
7) ;	8) ;	9) .
3. Tính các nguyên hàm và tích phân sau:
1) ;	2) ;	3) ;
4) ;	5) ;	6) ;
7) ;	8) ;	9) ;
10) .
4. Tính các nguyên hàm và tích phân sau:
1) ;	2) ;	3) 4) ;	5) ;	6) .
3. Nguyên hàm và tích phân các hàm vô tỉ
1) Nguyên hàm và tích phân các hàm số dạng , trong đó R là hàm hữu tỉ; m1, m2, , mk ẻ Z; n1, n2, , nk ẻ N*.
Cách giải: Đặt = t, với s là bội chung nhỏ nhất của các số n1, n2, , nk biến tích phân nói trên thành tích phân hàm hữu tỉ.
Ví dụ1. Tính tích phân I = 
Giải. ở đây n1 = 3, n2 = 2 ị s = 6. Đặt ị 2x + 1 = t6 ị dx = 3t5dt:
I = 
= .
Ví dụ 2. Tìm tích phân: 
Giải. Đặt ị x = t2 + 1; dx = 2tdt. Đưa tích phân đã cho về tính tích phân:
 = 2ln3 - 1.
2) Nguyên hàm và tích phân các hàm số dạng (a ≠ 0)
Tách bình phương đủ trong tam thức bậc hai rồi đưa về tìm nguyên hàm hoặc tích phân các hàm số dạng và .
Dễ dàng tìm được nguyên hàm của hàm số thứ nhất là . Để tính tích phân của hàm số thứ hai ta đặt x = a sint.
Ví dụ 1. Tìm nguyên hàm của hàm số .
Giải. Ta có: .
Ví dụ 2. Tính tích phân .
Giải. Ta có: . Đặt ị .
3) Nguyên hàm và tích phân hàm số dạng (a ≠ 0).
Ta phân tích: 
 = 
Ví dụ 1. Tìm nguyên hàm .
Giải. = =
= = .
Ví dụ 2. Tính tích phân: .
Giải. Ta có: =
= .
Đặt x - 3 = sint, , ta tính được .
Vậy .
4) Tích phân hàm số dạng 
Đặt sẽ đưa tích phân này về tích phân đã xét trong mục 2).
Ví dụ 1. Tính tích phân I = 
Giải. Đặt , khi đó và 
I = = .
Ví dụ 2. Tính tích phân J = 
Giải. Đặt , khi đó và . Do đó:
J = = = 
= .
5) Tích phân các hàm số dạng 
Phân tích: 
Ví dụ. Tính I = 
Giải. Ta có: I = .
Dễ dàng tính được tích phân thứ nhất bằng: .
Với tích phân thứ hai, ta đặt , ta có:
 = =
= = .
Vậy I = .
6) Tính tích phân hàm số dạng (n ≥ 2, an.a ≠ 0).
Để tính tích phân dạng trên ta làm như sau:
= , 
với Qn - 2(x) là đa thức bậc n - 2; m, n là các hằng số.
Để tính tích phân thứ nhất ta dùng phương pháp tích phân từng phần bằng cách đặt:
Đối với hàm số thứ hai, ta thấy ngay một nguyên hàm của nó là , tích phân thứ ba là tích phân có dạng 2)
Ví dụ. Tính tích phân I = 
Giải. Ta có: 
I = = = 
= 
Để tính tích phân thứ nhất, ta đặt:
Bài tập. Tính các tích phân
1) ;	2) ;	3) ;
4) ;	5) ;	6) ;
7) ;	8) ;	9) ;
10) .
7) Tích phân hàm số dạng 
Tách bình phương đúng trong tam thức bậc hai đưa về tính tích phân hàm số hoặc . Đối với hàm số thứ nhất để tính tích phân ta có thể dùng phương pháp tích phân từng phần, đối với hàm số thứ hai ta đặt x = a sint (hoặc x = a cost).
Ví dụ 1. Tính tích phân I = .
Giải. I = .
Đặt 
ị I = = 
ị I = .
Ví dụ 2. Tính J = 
Giải. Ta có J = . Đặt 2x - 1 = sin t, :
J = .
8) Tích phân các hàm số dạng 
Phép thế đưa tích phân đã cho về tích phân hàm hữu tỷ.
Ví dụ 1. Tính I = 
Giải. Đặt thì x = -1 Û , x = 1 Û và x2 + 1 = (t - x)2, tức là , do đó:
I = = = = 1.
Ví dụ 2. Tính J = 
Giải. Đặt , ta có:
J = 
= = 
= .
Nhận xét. Tích phân các hàm số dạng (ac > 0) bằng cách đặt (hoặc ) đưa được về tích phân dạng trên.
Ví dụ 3. Tính K = 
Giải. 
Đặt khi đó x = 0 Û t = 3, x = 2 Û và ị 
 ta có:
K = = .
Ví dụ 4. Tính tích phân 
Giải. Đặt ị 
ị 
L = = .
Cách khác : = = 
= .
Bài tập. Tính các tích phân
1) ;	2) ;	3) ;
4) ; 	
9) Tích phân các hàm số dạng , trong đó m, n, p là các số hữu tỉ.
Tích phân hàm số trên biễu diễn được bằng các hàm sơ cấp chỉ trong ba trường hợp sau:
a) p là số nguyên: Khi đó đặt (x = ts), với s là bội chung nhỏ nhất của các phân số m, n, tích phân sẽ được đưa về tích phân của hàm hữu tỷ.
b) là số nguyên: Đặt , với s là mẫu của p, sẽ đưa tích phân đã cho về tích phân của hàm hữu tỷ.
c) là số nguyên: Đặt , với s là mẫu của p, sẽ đưa tích phân đã cho về tích phân của hàm hữu tỷ.
Ví dụ 1. Tính tích phân I = 
Giải. Hàm số dưới dấu tích phân có thể viết , tức p = -10 ẻ Z. Do đó đặt
, khi đó x = t4 và dx = 4t3dt, ta có:
I = = 
= .
Ví dụ 2. Tính J = (a > 0)
Giải. Viết hàm số dưới dấu tích phân dưới dạng , ta được m = 3, n = 2, . Vì ẻ Z nên ta đặt (a2 - x2 = t2) ị xdx = -tdt và x2 = a2 - t2. Ta có:
J = .
Ví dụ 3. Tính K = 
Giải. ở đây m = -4, n = 2, ; ẻ Z. 
Đặt ị , ta có:
K = .
Ví dụ 4. Tính L = 
Giải. Viết tích phân dưới dạng L = . 
Đặt . Ta có:
L = = =
= 
Để tính ta đặt t = tgu thì .
Vậy L = .
Bài tập: Tính các tích phân
1) ;	2) ;	3) ;
4) ;	5) ;	6) .
4. Nguyên hàm và tích phân các hàm số lượng giác
1) Nguyên hàm và tích phân các hàm hữu tỷ đối với sinx và cosx: R(sinx, cosx)
Các tích phân này được đưa về tích phân hàm hữu tỷ nhờ phép thế “vạn năng” .
đối với phép thế này thì:
; .
Ví dụ 1. Tính tích phân I = 
Giải. Đặt , tích phân đã cho được đưa về tích phân 
I = = .
Nhận xét. Các tích phân hàm số dạng có thể tính dễ dàng nhờ phương pháp trên
Ví dụ 2. Tính 
Giải. Trước hết tìm các số A, B, C sao cho 
sinx + cosx + 1 = A(4sinx + 3cosx + 5) + B(4cosx - 3sinx) + C
hay sinx + cosx + 1 = (4A - 3B)sinx + (3A + 4B)cosx + 5A + C
ị 
Từ đó =
= = .
Ví dụ 2. Tính tích phân J = (ab ≠ 0, a ≠ b, a ≠ -b)
Giải. Với cách đặt trên ta có: 
J = = 
= .
Nhận xét: 
Nguyên hàm các hàm số dạng , , , tg(x+a) tg(x + b) có thể tính được theo cách trên, bằng cách làm như sau:
. Đặt , đưa về tìm nguyên hàm (mẫu thức có dạng m2u2 - n2).
.
Phép thế trong nhiều trường hợp đưa đến tính toán phức tạp, vì khi áp dụng nó sinx và cosx được biểu diễn qua t dưới dạng biểu thức hữu tỷ của t2.
Trong một số trường hợp việc tính tích phân dạng trên có thể đơn giản hơn
+) Nếu R(sinx, cosx) là hàm lẻ đối với sinx, tức là R(-sinx, cosx) = -R(sinx, cosx), thì có thể tính tích phân bằng cách thế cosx = t.
+) Nếu R(sinx, cosx) là hàm lẻ đối với cosx, tức là R(sinx, -cosx) = -R(sinx, cosx), thì có thể tính tích phân bằng cách thế sinx = t.
+) Nếu R(sinx, cosx) là hàm chẵn đối với sinx và cosx, tức là R(-sinx, -cosx) = R(sinx, cosx), thì có thể tính tích phân bằng cách thế tgx = t.
Ví dụ 3. Tìm nguyên hàm của hàm số .
Giải. Vì hàm số đã cho là lẻ đối với sinx nên ta đặt cosx = t. Từ đó sinx dx = -dt, sin2x = 1 - t2, cos2x = 2t2 - 1. Vậy
 = =
= .
Chú ý. Trong trường hợp này hàm số đã cho luôn viết được dưới dạng R*(sin2x, cosx)sinx dx.
Ví dụ 4. Tính K = 
Giải. Hàm đã cho là lẻ đối với cosx. Đặt sinx = t, ta có cosx dx = dt, cos2x = 1 - t2. Do đó:
K = =
= .
Chú ý. Trong trường hợp này hàm số đã cho luôn viết được dưới dạng R*(cos2x, sinx)cosx dx.
Ví dụ 5. Tính L = 
Giải. Hàm dưới dấu tích phân chẵn đối với sinx và cosx. Ta đặt tgx = t, khi đó , . Từ đó
L = .
Nhận xét. Tích phân các hàm số dạng R(tgx), R là hàm hữu tỷ chính là tích phân dạng trên
Ví dụ 6. Tính tích phân 
Giải. Đặt tgx = t ị , đưa tích phân đã cho về tích phân 
 = = 
= = .
2) Nguyên hàm và tích phân các hàm số dạng sinmx.cosnx.
Ta xét hai trường hợp có ý nghĩa đặc biệt quan trọng
Trường hợp 1. ít nhất một trong các số mũ m hoặc n là số lẻ dương
Nếu n lẻ dương thì đặt sinx = t; còn nếu m là số lẻ dương thì đặt cosx = t.
Trường hợp 2. Cả hai số m, n đều là số dương chẵn
Cần biến đổi hàm dưới dấu tích phân nhờ các công thức sau
.
Ví dụ 1. Tìm nguyên hàm 
Giải. Đặt sinx = t, cosx dx = dt, ta được:
= .
Ví dụ 2. Tính tích phân I = 
Giải. ở đây m = 3 là số lẻ dương. Đặt cosx = t, - sinx dx = dt. Ta có:
I = = .
Ví dụ 3. Tìm nguyên hàm của hàm số sin2x.cos2x
Giải. Ta có . Do đó nguyên hàm của nó là:
.
Ví dụ 4. Tính tích phân J = .
Giải. Ta có: J = =
= = 
= = .
Ví dụ 5. Tìm họ nguyên hàm của hàm số sin2x.cos4x.
Giải. Ta có 
sin2x.cos4x = (sinx cosx)2cos2x = 
Do đó: =
	 = .
3) Nguyên hàm và tích phân các hàm số dạng tgmx, cotgmx, trong đó m là số nguyên dương
Trong trường hợp này ta dùng công thức hoặc để hạ liên tiếp bậc của tang và côtang.
Ví dụ. Tìm họ nguyên hàm các hàm số sau:
a) tg7x;	b) cotg6x.
Giải. a) Ta có: 
= = = 
= .
b) = 
= =
= .
4) Nguyên hàm và tích phân các hàm số dạng , trong đó n là số dương chẵn
Đối với nguyên hàm và tích phân dạng này ta dùng các công thức 
 hoặc .
Ví dụ 1. Tìm nguyên hàm 
Giải. Ta có = 
= .
Ví dụ 2. Tìm nguyên hàm 
Giải. Ta có: .
5) Tính các tích phân dạng , với n nguyên dương.
Để tính các tích phân trên ta dùng phương pháp tích phân từng phần hoặc đưa về tích phân hàm hữu tỷ bằng cách đặt cosx = t (đối với tích phân thứ nhất), sinx = t (đối với tích phân thứ hai)
Nếu dùng phương pháp tích phân từng phần thì:
Đối với tích phân thứ nhất ta đặt 
Đối với tích phân thứ nhất ta đặt 
Ta có: 
= 
Từ đó suy ra: 
 (1)
Tương tự như vậy, ta có:
 (2)
Ví dụ 1. Tính tích phân I = .
Giải. áp dụng (2) với n = 2, ta được
Lại áp dụng (2) với n = 1, ta có:
 = .
Vậy: .
Ví dụ 2. Tính tích phân J = 
Giải. áp dụng (1) với n = 1, ta có:
J = . 
Nhận xét. Các tích phân trên có thể tính được bằng cách khác như sau:
;
.
Chẳng hạn, ta có thể tính nguyên hàm của hàm số như sau:
. Đặt sinx = t, ta có: 
 =
= C.
6) Nguyên hàm và tích phân các hàm số dạng sin mx.cos nx; cos mx.cos nx; sin mx.sin nx.
Biến đổi hàm số về dạng tổng bằng các công thức
.
Ví dụ 1. Tìm họ nguyên hàm của hàm số sin2x cos5x.
Giải. Ta có: sin2x cos5x = . Do đó họ nguyên hàm của hàm số đó là:
.
Ví dụ 2. Tìm họ nguyên hàm của hàm số .
Giải. Ta có: =
= .
Từ đó suy ra họ nguyên hàm hàm số đã cho là: .
7) Phép thế lượng giác. Các nguyên hàm và tích phân hàm số dạng 
; ; 
được đưa về tích phân các hàm hữu tỷ đối với sinx và cosx nhờ các phép thế lượng giác thích hơp: Đối với tích phân thứ nhất đặt x = a sint (hoặc x = a cost), đối với tích phân thứ hai x = a tgt (hoặc x = a cotgt), đối với tích phân thứ ba (hoặc ).
Ví dụ 1. Tính tích phân I = 
Giải. Đặt x = a sint, , khi đó dx = a cost dt. Ta có
I = = 
= .
Ví dụ 2. Tính J = 
Giải. Đặt x = a tg t , khi đó và 
J = = 
= .
Ví dụ 3. Tính K = 
Giải. Đặt ị . Ta có:
K = 
= = .
Nhận xét. Có thể tính tích phân trên bằng cách đặt .
5. Một vài tích phân khác
1) Phương pháp tích phân từng phần
Các tích phân dạng .
Để tính các tích phân trên ta dùng phương pháp tích phân từng phần: Đối với tích phân sau cùng thì nên đặt u = lnx, dv = P(x) dx; đối với các tích phân còn lại thì nên đặt u = P(x), dv = sinx, dv = cosx hoặc dv = ex.
Ví dụ 1. Tính các tích phân
1) I = ;	2) J = ;	3) K =.
Giải. 1) Đặt 
Ta có: I = .
Để tính ta tiếp tục đặt 
ị = .
Vậy I = .
2) Đặt 
Ta có: J = .
Để tính ta đặt 
ị .
Vậy J = .
3) Đặt 
Ta có: K = 
= .
Ví dụ 2. Tính các tích phân sau
1) ;	2) ;	3) ;
4) ;	5) ;	6) ;
7) .
Giải. 1) Đặt 
Ta có: .
Tiếp tục đặt 
ị .
Vậy .
2) Đặt 
Ta có: =
= .
3) Đặt 
ị .
Để tính ta đặt , khi đó:
 =
= .
Vậy .