Chuyên đề Lượng Giác (GV Lê Thị Nhung)
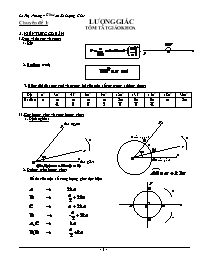
III. Định nghĩa hàm số lượng giác:
1. Đường tròn lượng giác:
• A: điểm gốc
• x'Ox : trục côsin ( trục hoành )
• y'Oy : trục sin ( trục tung )
• t'At : trục tang
• u'Bu : trục cotang
Bạn đang xem tài liệu "Chuyên đề Lượng Giác (GV Lê Thị Nhung)", để tải tài liệu gốc về máy bạn click vào nút DOWNLOAD ở trên
Chuyên đề 1: LƯỢNG GIÁC TÓM TẮTGIÁO KHOA A. KIẾN THỨC CƠ BẢN: . I. Đơn vị đo góc và cung: 1. Độ: 2. Radian: (rad) 3. Bảng đổi độ sang rad và ngược lại của một số góc (cung ) thông dụng: Độ 00 300 450 600 900 1200 1350 1500 1800 3600 Radian 0 II. Góc lượng giác và cung lượng giác: (điểm gốc) (điểm ngọn) (tia gốc) (tia ngọn) 1. Định nghĩa: 2. Đường tròn lượng giác: Số đo của một số cung lượng giác đặc biệt: III. Định nghĩa hàm số lượng giác: 1. Đường tròn lượng giác: A: điểm gốc x'Ox : trục côsin ( trục hoành ) y'Oy : trục sin ( trục tung ) t'At : trục tang u'Bu : trục cotang 2. Định nghĩa các hàm số lượng giác: a. Định nghĩa: Trên đường tròn lượng giác cho AM= . Gọi P, Q lần lượt là hình chiếu vuông góc của M trên x'Ox và y'Oy Trục cosin Trục tang Trục sin Trục cotang T, U lần lượt là giao điểm của tia OM với t'At và u'Bu Ta định nghĩa: b. Các tính chất : Với mọi ta có : c. Tính tuần hoàn IV. Giá trị các hàm số lượng giác của các cung (góc ) đặc biệt: Ta nên sử dụng đường tròn lượng giác để ghi nhớ các giá trị đặc biệt Góc Hslg 00 300 450 600 900 1200 1350 1500 1800 3600 0 sin 0 1 0 0 cos 1 0 -1 1 tan 0 1 KXĐ -1 0 0 cot KXĐ 1 0 -1 KXĐ KXĐ V. Hàm số lượng giác của các cung (góc) có liên quan đặc biệt: Đó là các cung : 1. Cung đối nhau : (tổng bằng 0) (Vd: ,) 2. Cung bù nhau : ( tổng bằng ) (Vd: ,) 3. Cung phụ nhau : ( tổng bằng ) (Vd: ,) 4. Cung hơn kém : (Vd: ,) 5. Cung hơn kém : (Vd: ,) 1. Cung đối nhau: 2. Cung bù nhau : Bù sin Đối cos 3. Cung phụ nhau : 4. Cung hơn kém Phụ chéo Hơn kém sin bằng cos cos bằng trừ sin 5. Cung hơn kém : Hơn kém tang , cotang Ví dụ 1: Tính . Ví dụ 2: Rút gọn biểu thức: VI. Công thức lượng giác: 1. Các hệ thức cơ bản: Ví du: Chứng minh rằng: 1. 2. 2. Công thức cộng : Ví du: Chứng minh rằng: 3. Công thức nhân đôi: 4 Công thức nhân ba: 5. Công thức hạ bậc: 6.Công thức tính theo 7. Công thức biến đổi tích thành tổng : Ví dụ: 1. Biến đổi thành tổng biểu thức: 2. Tính giá trị của biểu thức: 8. Công thức biến đổi tổng thành tích : Ví dụ: Biến đổi thành tích biểu thức: 9. Các công thức thường dùng khác: B. PHƯƠNG TRÌNH LƯỢNG GIÁC Các bước giải một phương trình lượng giác Bước 1: Tìm điều kiện (nếu có) của ẩn số để hai vế của pt có nghĩa Bước 2: Sử dụng các phép biến đổi tương đương để biến đổi pt đến một pt đã biết cách giải Bước 3: Giải pt và chọn nghiệm phù hợp ( nếu có) Bước 4: Kết luận I. Định lý cơ bản: ( Quan trọng ) ( u; v là các biểu thức chứa ẩn và ) Ví dụ : Giải phương trình: 1. 2. 3. 4. II. Các phương trình lượng giác cơ bản: 1. Dạng 1: sinx = a ; cosx = a ; tanx = a ; cotx = a ( ) * Gpt : sinx = a (1) Nếu thì pt(1) vô nghiệm. Nếu thì ta đặt a = sin và ta có : () * Gpt : cosx = a (2) Nếu thì pt(2) vô nghiệm Nếu thì ta đặt a = cos và ta có () * Gpt: tan x = a (3) ( pt luôn có nghiệm ) Đặt a = tan thì () * Gpt: cot x = a (4) ( pt luôn có nghiệm ) Đặt a = cot thì () Các trường hợp đặc biệt: () Ví dụ: 1) Giải các phương trình : a) b) c) d) e) f) 2) Giải các phương trình: a) c) b) d) e) 2. Dạng 2: ( ) Cách giải: Đặt ẩn phụ : t = sinx ( t = cosx; t = tanx; t = cotx) Ta được phương trình : (1) Giải phương trình (1) tìm t, rồi suy ra x Chú ý : Phải đặt điều kiện thích hợp cho ẩn phụ (nếu có) Ví dụ : a) b) c) d) e) f) g) h) k) l) 3. Dạng 3: Cách giải: Chia hai vế của phương trình cho thì pt (2) Đặt với thì : Pt (3) có dạng 1. Giải pt (3) tìm x. Chú y : Ví dụ : Giải các phương trình : a) b) c) d) e) d. Dạng 4: (1) Cách giải 1: Ap dụng công thức hạ bậc : và công thức nhân đôi : thay vào (1) ta sẽ biến đổi pt (1) về dạng 3 Cách giải 2: ( Quy về pt theo tang hoặc cotang ) Chia hai vế của pt (1) cho ta được pt: Đây là pt dạng 2 đã biết cách giải Chú ý: Trước khi chia phải kiểm tra xem có phải là nghiệm của (1) không? Ví dụ : Giải phương trình: d. Dạng 5: (1) Cách giải : Đặt Do Thay vào (1) ta được phương trình : (2) Giải (2) tìm t . Chọn t thỏa điều kiện rồi giải pt: tìm x. Ví dụ : Giải phương trình : Chú ý : Ta giải tương tự cho pt có dạng : Ví dụ : Giải phương trình : 4. Các phương pháp giải phương trình lượng giác thường sử dụng : a. Phương pháp 1: Biến đổi pt đã cho về một trong các dạng pt lượng giác cơ bản đã biết Ví dụ: Giải phương trình: b. Phương pháp 2: Biến đổi pt đã cho về dạng tích số Cơ sở của phương pháp là dựa vào các định lý sau đây: hoặc Ví du : Giải các phương trình : a. b. c. d. c. Phương pháp 3: Biến đổi pt về dạng có thể đặt ẩn số phụ Một số dấu hiệu nhận biết : * Phương trình chứa cùng một một hàm số lượng giác ( cùng cung khác lũy thừa) Ví dụ : Giải các phương trình : a. b. c. d. * Phương trình có chứa Ví dụ : Giải phương trình : a. b. C. BÀI TẬP RÈN LUYỆN Giải phương trình lượng giác Sử dụng 1 trong 3 phương pháp sau Biến đổi phương trình về dạng phương trình lượng giác cơ bản Biến đổi phương trình về dạng phương trình tích số Biến đổi phương trình về dạng có thể đặt ẩn số phụ chuyển về phương trình đại số Bài 1: Giải các phương trình lượng giác sau 1) ; 2) ; 3) ; 4) ; 5) ; 6) . Bài 2 : Giải các phương trình lượng giác sau 1. ; 8. ; 2. ; 9. ; 3. ; 10. ; 4. ; 11. ; 5. ; 12. ; 6. ; 13. ; 7. ; 14. . Bài 3: Giải các phương trình sau: Bài 4: Giải các phương trình sau: Bài 5: Giải các phương trình sau: Bài 6: Giải các phương trình sau: Bài 7: Giải các phương trình sau: 1) sin2x – 2cosx = 0 2) 2sin2x + cos3x = 1 3) 2cos2x + cos2x = 2 4) 8cos2xsin2xcos4x = 5) tan2x – tanx = 0 6) cos2(x – 300) = Bài 8: Giải các phương trình sau: 1) sin2x + 2sinx – 3 = 0 2) 2sin2x + sinx – 1 = 0 3) 2sin22x + 5sin2x + 2 = 0 4) 2cos2x – 3cosx – 2 = 0 5) 4cos2x + 4cosx – 3 = 0 6) 2cos2x – 5cosx – 3 = 0 7) 3tan2x – tanx – 4 = 0 8) 5 + 3tanx – tan2x = 0 9) -5cot2x – 3tanx + 8 = 0 Bài 9: Giải các phương trình sau: 1) 3sin22x + 7cos2x – 3 = 0 2) 5sin2x + 3cosx + 3 = 0 3) 6cos2x + 5sinx – 7 = 0 4) 3cos2x – 2sinx + 2 = 0 5) 6) cos2x – 5sinx – 3 = 0 7) cos2x + cosx + 1 = 0 8) 3sin2x – 4cos4x = -1 9) 5cosx – 6cos2x = 2 10) 2cos2x – sin2x – 4cosx + 2 = 0 11) 9sin2x – 5cos2x – 5sinx + 4 = 0 12) cos2x + sin2x + 2cosx + 1 = 0 13) 3cos2x + 2(1 + + sinx)sinx – 3 - = 0 14) sin2x - cos2x + 4sinx = 6 15) sin22x – 2cos2x + = 0 16) sin3x + 3sin2x + 2sinx = 0 17) 18) 3tanx – 4cotx + 1 = 0 Bài 10: Giải các phương trình sau: 1) sinx - cosx = 2) 3) 2sin2x +sin2x = 3 4) 2cosx – sinx = 2 5) sin5x + cos5x = -1 6) sin6x + cos6x + sin4x = 0 7) 1 + sinx – cosx –sin2x + 2cos2x = 0 8) 8cos4x – 4cos2x + sin4x – 4 = 0 Bài 11: Giải các phương trình sau: 1) sin2x – 2sinxcosx – 3cos2x = 0 2) 6sin2x + sinxcosx – cos2x = 2 3) sin2x – 2sin2x = 2cos2x 4) 2sin2x – 3sin4x + cos22x = 2 5) 4cos2x +3sinxcosx - sin2x = 3 6) 4sin2x – 4sinxcosx + 3cos2x = 1 VÍ DỤ VỂ CÁC BÀI TẬP PHƯƠNG TRÌNH LƯỢNG GIÁC TRONG CÁC ĐỀ THI ĐẠI HỌC TỪ 2002 ĐẾN 2009 KHỐI A Tìm nghiệm thuộc khoảng (0;2p) của phương trình: (Khối A_2002). ĐS: . Giải phương trình: Khối A_2003) ĐS: Giải phương trình: (Khối A_2005) ĐS: Giải phương trình: (Khối A_2006) ĐS: Giải phương trình: (Khối A_2007) ĐS: (Khối A_2008) ĐS: Giải phương trình: . (Khối A_2009) ĐS: KHỐI B Giải phương trình (Khối B_2002) ĐS: Giải phương trình (Khối B_2003) ĐS: Giải phương trình (Khối B_2004) ĐS: Giải phương trình (Khối B_2005) ĐS: Giải phương trình: (Khối B_2006) ĐS: Giải phương trình: (Khối B_2007) ĐS: Giải phương trình (Khối B_2008) ĐS: Giải phương trình: . (Khối B_2009) ĐS: KHỐI D Tìm xÎ[0;14] cos3x-4cos2x+3cosx-4=0 (Khối D_2002) ĐS: (Khối D_2003) ĐS: Giải phương trình (Khối D_2004) ĐS: Giải phương trình: (Khối D_2005) ĐS: Giải phương trình: cos3x+cos2x-cosx-1=0 (Khối D_2006) ĐS: Giải phương trình (Khối D_2007) ĐS: Giải phương trình (CĐ_A_B_D_2008) ĐS: Giải phương trình 2sinx(1+cos2x)+sin2x=1+2cosx (Khối D_2008) ĐS: Giải phương trình (1+2sinx)2cosx=1+sinx+cosx (CĐ_A_B_D_2009) ĐS: Giải phương trình (Khối D_2009) ĐS: -Hết-
Tài liệu đính kèm:
 3-[Nhung]_LUONG_GIAC.doc
3-[Nhung]_LUONG_GIAC.doc





