Chuyên đề Hình học 12 Quan hệ vuông góc
Chứng minh hai đường thẳng a và b vuông góc nhau:
* Cách 1: áp dụng định nghĩa:
a vuông góc b tương đương (a,b) = 90 độ
* Cách 2: a vuông góc b tương đương i.v = 0 ( u, v là các véc-tơ chỉ phương của a và b)
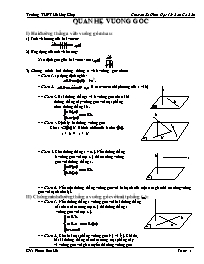
* * Cách 3: Hai đường thẳng a và b vuông góc nhau khi
đường thẳng này vuông góc với mặt phẳng
chứa dường thẳng kia.
a vuông góc (alpha)
b chứa (alpha) suy ra a vuông góc b
* * Cách 4: Định lý ba đường vuông góc
Cho a chứa (alpha), b’ là hình chiếu của b trên (alpha) .
a vuông góc b tương đương a vuông góc b’
Bạn đang xem tài liệu "Chuyên đề Hình học 12 Quan hệ vuông góc", để tải tài liệu gốc về máy bạn click vào nút DOWNLOAD ở trên
QUAN HEÄ VUOÂNG GOÙC I) Hai đường thẳng a và b vuông góc nhau: 1) Tích vô hướng của hai véc-tơ: () 2) Ứng dụng của tích vô hướng: Xác định góc giữa hai vectơ: cos() = 3) Chứng minh hai đường thẳng a và b vuông góc nhau: * Cách 1: áp dụng định nghĩa: = 900 . a b a b a b b’ a a a b a c * Cách 2: ( là các véc-tơ chỉ phương của a và b) * * Cách 3: Hai đường thẳng a và b vuông góc nhau khi đường thẳng này vuông góc với mặt phẳng chứa dường thẳng kia. * * Cách 4: Định lý ba đường vuông góc Cho a , b’ là hình chiếu của b trên . a ^ b Û a ^ b’ * Cách 5: Cho đường thằng a // (a). Nếu đường thẳng b vuông góc với mp (a) thì nó cũng vuông góc với đường thẳng a . * * Cách 6: Nếu một đường thẳng vuông góc với hai cạnh của một tam giác thì nó cũng vuông góc với cạnh còn lại. II) Chứng minh đường thẳng a vuông góc với mặt phẳng (a): * * Cách 1: Nếu đường thẳng a vuông góc với hai đường thẳng cắt nhau nằm trong mp (a) thì đường thẳng a vuông góc với mp (a). * * Cách 2: Cho hai mặt phẳng vuông góc (a) và (b). Khi đó, bất kì đường thẳng nào nằm trong mặt phẳng này và vuông góc với giao tuyến thì cũng vuông góc a b b a a b a a b a b b’ a O a a’ a với mp còn lại. * Cách 3: Nếu hai mp cắt nhau cùng vuông góc với mp thứ ba thì giao tuyến của chúng vuông góc với mp thứ ba. III) Chứng minh hai mặt phẳng (a) ^ (b): * Cách 1: áp dụng định nghĩa: (a) ^ (b) Û góc giữa chúng bằng 900. * * Cách 2: Hai mặt phẳng vuông góc khi và chỉ khi mặt phẳng này có chứa một đường thẳng vuông góc với mặt phẳng còn lại. Û (a) ^ (b) IV) GÓC: 1) Góc giữa hai đường thẳng: a Góc giữa hai đường thẳng trong không gian là góc a’ giữa hai đường thẳng a’ và b’ cùng đi qua một điểm và lần lượt song song với a và b. b’ (a, b) = (a’, b’) b Chú ý: Để dựng góc giữa hai đường thẳng chỉ cần lấy điểm O trên a từ đó kẻ đường thẳng b’ // b. Khi đó, góc giữa a và b chính là góc giữa a và b’. b // b’ Þ (a, b) = (a’, b’) 2) Góc giữa đường thẳng a và mp (a): Đ/n: Góc giữa đường thẳng a và mp (a) bằng góc giữa đường thẳng a và hình chiếu a’ của nó trên mp (a). (a, (a)) = (a, a’) với a’ là hình chiếu của a trên (a). 3) Góc giữa hai mặt phẳng (a) và (): Các bước xác định góc: a b a b c + Xác định giao tuyến c của (a) và () + Xác định hai đường thẳng a và b lần lượt nằm trên hai mặt phẳng (a) và () đồng thời cùng vuông góc với giao tuyến c + Xác định góc giữa a và b. ( góc giữa a và b là góc giữa (a) và () ) O H a V) KHOẢNG CÁCH: 1) Khoảng cách từ điểm O đến đường thẳng a: Gọi H là hình chiếu vuông góc của O trên a Khi đó: d(O, a) = OH O H a 2) Khoảng cách từ điểm O đến mp (a): Gọi H là hình chiếu vuông góc của O trên (a) Khi đó: d(O, (a)) = OH O a H a 3) Khoảng cách giữa đường thẳng và mp song song: Cho đường thẳng a song song với mp (a). Khoảng cách giữa đường thẳng a song song với mp (a) bằng khoảng cách từ một điểm bất kì trên a đến mp (a). d(a, (a)) = d(O, (a)) = OH , " O a O H a b 4) Khoảng cách giữa hai mp song song: Cho hai mp song song (a) và (). Khoảng cách giữa (a) và () bằng khoảng cách từ một điểm bất kì trên mp này đến mp còn lại. d((a), () ) = d(O, (a)) = OH " O 5) Khoảng cách giữa hai đường thẳng chéo nhau: a b M N * Khoảng cách giữa hai đường thẳng chéo nhau bằng độ dài đoạn vuông góc chung của chúng. d( a, b) = MN, với MN là đoạn vuông góc chung * Khoảng cách giữa hai đường thẳng chéo nhau bằng khoảng cách giữa đường thẳng này với mặt phẳng song song chứa đường thẳng còn lại. M a N a b d(a, b) = d(a, (a)), với (a) chứa b và song song a * Khoảng cách giữa hai đường thẳng chéo nhau bằng khoảng cách giữa hai mp song song lần a b b a M N lượt chứa hai đường thẳng đó. d(a, b) = d((a), ()) , với (a), () song song lần lượt chứa a, b S A B C D S A B C * * Một số dạng hình thường gặp: S A B C D Hình chóp đáy tam giác Hình chóp đáy tứ giác Hình chóp đáy hình thang A B C S S A B C D Hình chóp có đáy là hbh, ht, hcn, hv Hình chóp đáy tam giác có SA ^ đáy S A B C D S A B C D Hình chóp đáy hình thang có SA ^ đáy Hình chóp đáy là hbh, ht, hcn, hv có SA ^ đáy B S A H C I S A C B D H A B C D A’ B’ C’ D’ A B C D A’ B’ C’ D’ Hình choùp ñeàu ñaùy tam giaùc Hình choùp ñeàu ñaùy töù giaùc A B C A’ C’ B’ Lăng trụ đứng tam giác Hình hộp chữ nhật Hình lập phương BÀI TẬP 1/ Cho hình chóp S.ABCD có đáy là hình vuông ABCD cạnh a, SA = a và vuông góc với đáy. CMR: các mặt bên của hình chóp là các tam giác vuông Mặt phẳng (P) đi qua A và vuông góc với SC cắt SB, SC, SD tại B’, C’, D’. CMR: B’D’ // BD và AB’ ^ SB, AD’ ^ SD. 2/ Cho hình chóp S.ABCD có đáy là hình thoi cạnh a và có góc BAD = 600 . Gọi O là giao điểm của AC và BD, đường thẳng SO vuông góc với mặt phẳng (ABCD) và SO = . Gọi E là trung điểm BC, F là trung điểm của BE. CMR: (SOF) ^ (SBC) Tính khoảng cách từ O và A đến mp (SBC) 3/ Cho tứ diện ABCD có hai mặt (ABC) và (ADC) nằm trong hai mặt phẳng vuông góc nhau. Tam giác ABC vuông tại A có AB = a, AC = b. Tam giác ADC vuông tại D có CD = a. CMR: tam giác BAD và BDC là các tam giác vuông Gọi I, K là trung điểm của AD và BC. CM: IK là đường vuông góc chung của AD và BC. 4/ Cho hình chóp S.ABCD có đáy là hình thoi cạnh a và có góc BAD = 600 và SA = SB = SD = Tính khoảng cách từ S đến mp (ABCD) và độ dài cạnh SC CMR: (SAC) ^ (ABCD) CMR: SB ^ BC Gọi a là góc giữa hai mặt phẳng (SBD) và (ABCD). Tính tana. CHƯƠNG I. THỂ TÍCH KHỐI ĐA DIỆN I) Kiến thức cơ bản: Thể tích khối hộp chữ nhật: V = abc (tích ba kích thước) Thể tích khối lập phương: V = a3 3) Thể tích khối lăng trụ: V = B.h Trong đó: B là diện tích đáy, h là chiều cao của khối lăng trụ 4) Thể tích khối chóp: V = B.h Trong đó: B là diện tích đáy, h là chiều cao của khối chóp. II) Bài tập: A. Bài toán 1: Thể tích khối lăng trụ. Ví dụ: Cho lăng trụ ABC.A’B’C’ có đáy là tam giác đều cạnh a, AA’ = b và AA’ tạo với mặt đáy một góc 600. Tính thể tích khối lăng trụ . A A’ C B B’ C’ H 600 Giải Gọi H là chân đường cao kẻ từ A của lăng trụ. Khi đó, A’H là hình chiếu của AA’ trên mp(A’B’C’) Xét tam giác AA’H vuông tại H có: Sin A’ = AH = AA’. Sin A’ = AA’. Sin 600 = Do tam giác A’B’C’ là tam giác đều nên chiều cao của tam giác là: h = Diện tích tam giác A’B’C’: SA’B’C’ = Thể tích ABC.A’B’C’: V = .AH. SA’B’C’ = BÀI TẬP Bài 1. Cho lăng trụ đứng ABC.A1B1C1, đáy ABC là tam giác vuông tại A, AC= a, góc C bằng 600, đường chéo BC1 của mặt bên (CC1B1) hợp với mặt bên (ACC1A1) một góc 300. a. Tính độ dài đoạc AC1. b. Tính thể tích khối lăng trụ ĐS: a. AC1 = 3a, b. V = a3. Bài 2. Cho hình hộp đứng ABCD.A1B1C1D1 , đáy là hình thoi. Biết diện tích 2 mặt chéo ACC1A1 và BĐ1B1 là s1 và s2. Biết góc BA1D là góc vuông. Tính thể tích khối hộp. ĐS: V = Bài 3. Cho lăng trụ tam giác ABC.A1B1C1, đáy ABC là tam giác đều cạnh a. Hình chiếu của A1 lên mp(ABC) trùng với tâm đường tròn ngoại tiếp tam giác ABC. Cạnh bên AA1 tạo với mặt đáy một góc 600. a. Tính thể tích lăng trụ. b. Chứng minh: BCC1B1 là hình chữ nhật c. Tính diện tích xung quanh của lăng trụ ĐS: a. V = , c. Sxq= Bài 4. Cho hình hộp ABCD.A1B1C1D1 , đáy là hình thoi cạnh a, góc A bằng 600. Chân đường vuông góc hạ từ B1 xuống mặt đáy ABCD trùng với giao điểm hai đường chéo của đáy. Cho BB1= a a. Tính góc giữa cạnh bên và đáy b. Tính thể tích khối hộp ĐS: a. 600, b. V= Bài 5. Cho lăng trụ đều ABCD.A1B1C1D1 cạnh đáy bằng a. Góc giữa đường chéo AC1 và đáy là 600. Tính thể tích của khối lăng trụ. Bài 6. Cho lăng trụ tứ giác đều ABCD.A1B1C1D1 có đường cao bằng h. Mp (A1BD) hợp với mặt bên (ABB1A1) một góc a. Tính thể tích của khối lăng trụ. Bài 7. (đề thi ĐH khối D-2008) Cho lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác vuông, AB = BC = a, cạnh bên AA’ = a. Gọi M là trung điểm của cạnh BC. Tính theo a thể tích của khối lăng trụ ABC.A’B’C’ và khoảng cách giữa hai đường thẳng AM, B’C. ĐS: V = , d(AM, B’C) = Bài 8. Cho hình hộp chữ nhật ABCD.A1B1C1D1 có AB = a, AB hợp với mặt phẳng (A’B’CB) một góc a và góc BAC’ = b. Tính thể tích hình hộp. Bai 9. Cho lăng trụ tam giác đều ABC.A1B 1C1 , cạnh đáy a. Mặt phẳng (ABC1) hợp với mặt phẳng (BCC1B1) một góc a. Gọi I, J là hình chiếu của A lên BC và BC1. a. CM: góc AJI bằng a. b. Tính thể tích khối lăng trụ Bài 10. Cho lăng trụ tam giác đều ABC.A1B1C1 , cạnh đáy bằng a, đường chéo BC1 của mặt bên (BCC1B1) hợp với mặt bên (ABB1A1) một góc a. a. Xác định góc a b. Tính thể tích khối lăng trụ. Bài 11. Cho lăng tru đứng ABC.A1B1C1 , đáy ABC là tam giác cân tại A. Góc giữa AA1 và BC1 là 300 và khoảng cách giữa chúng là a. Góc giữa hai mặt bên qua AA1 là 600. Tính thể tích khối lăng trụ. Bài 12. Cho lăng trụ đều ABC.A1B1C1. Mặt phẳng (A1BC) cách A một khoảng và hợp với BC’ một góc a biết sin a = . Tính thể tích khối lăng trụ. Bài 13. Cho lăng tru đứng ABC.A1B1C1 , đáy ABC là tam giác vuông tại A, AC= b, góc C bằng a. Đường chéo BC1 tạo với mặt bên (ACC1A1) một góc b. a. Tính thể tích khối lăng trụ b. Tìm một điểm cách đều các đỉnh của lăng trụ và tính khoảng cách ấy. Bài 14. Cho lăng trụ ABC.A1B1C1 đáy là tam giác đều cạnh a. Hình chiếu của A1 lên mặt phẳng (ABC) trùng với tâm đường tròn (ABC). Góc BAA1 bằng 450. Tính thể tích khối lăng trụ. Bài 15. Cho lăng trụ xiên ABC.A1B1C1 đáy là tam giác vuông cân tại A. Mặt bên (ABB1A1) là hình thoi cạnh a, nằm trong mặt phẳng vuông góc với đáy. Mặt bên (ACC1A1) hợp với đáy một góc a. Tính thể tích khối lăng trụ Bài 16. Cho lăng trụ xiên ABC.A1B1C1 đáy ABC là tam giác vuông tại A. AB = a, BC = 2a. Mặt bên ABB1A1 là hình thoi, mặt bên (BCC1B1) nằm trong mặt phẳng vuông với đáy, hai mặt này hợp với nhau một góc a. a. Tính khoảng cách từ A đến mp (BCC1B1). Xác định góc a b . Tính thể tích khối lăng trụ. Bài 17. Tính thể tích của khối lăng trụ có chiều cao h, đáy là ngũ giác đều nội tiếp trong một đường tròn bán kính bằng r. B. Bài toán 2: Tính thể tích khối chóp. Ví dụ: Cho khối chóp tam giác đều S.ABC có đáy là tam giác đều cạnh a, các cạnh bên hợp với đáy A B C S I H một góc 600. Tính thể tích của khối chóp đó. Giải Kẻ SH (ABC) Gọi I là giao điểm của AH và BC Do S.ABC là hình chóp đều nên H là trọng tâm của tam giác ABC. Þ AI = Þ AH = AI = Do AH là hình chiếu của SA trên mp(ABC) nên SAH = 600. Xét tam giác SAH vuông tại H ta có: tan 600 = = a Diện tích tam giác ABC: SABC = = Thể tích khối chóp: V = SH. SABC = BÀI TẬP Bài 1. Cho khối chóp tam giác đều SABC có đáy là tam giác đều cạnh bằng a, các cạnh bên hợp với đáy một góc 300. Tính thể tích của khối chóp đó. Bài 2. Cho khối chóp SABC có đáy là tam giác cân, AB = AC = 5a, BC = 6a và các mặt bên tạo với đáy một góc 600. Tính thể tích của khối chóp đó. Bài 3. Cho khối chóp SABC có đáy là tam giác vuông tại B. Cạnh bên SA vuông góc với đáy. Từ A kẻ các đoạn thẳng AD vuông góc với SB và AE vuông góc với SC. ... là một điểm nằm trên mặt đáy và cách O một đoạn bằng 2r. Trong hình tròn tâm O kẻ bán kính OA vuông góc với OI. IA cắt đường tròn tại B. Tính thể tích khối nón và diện tích xung quanh của hình nón. Bài 5. Cho hình nón có đỉnh D, O là tâm đường tròn đáy, đường sinh bằng l và góc giữa đường sinh và mặt đáy bằng a. Tính diện tích của hình nón và thể tích của khối nón được tạo nên. Bài 6. Cho hình chóp tứ giác đều SABCD có chiều cao h và góc SAB = a (a > 450). Tính diện tích xung quanh của hình nón đỉnh S và có đường tròn đáy ngoại tiếp hình vuông ABCD của hình chóp. Bài 7. Cho khối nón có bán kính đáy bằng 12 cm và có góc ở đỉnh là 1200. Hãy tính diện tích thiết diện đi qua hai đường sinh vuông góc với nhau. Bài 8. Một mặt phẳng (P) qua đỉnh của hình nón cắt đường tròn đáy theo một cung có số đo là a (a<). Biết rằng (P) hợp với mặt đáy một góc b và khoảng cách từ tâm của đáy tới (P) bằng a. Tính thể tích khối nón theo a, a, b. II) MẶT TRỤ, HÌNH TRỤ, KHỐI TRỤ: DẠNG 1: Chứng minh một điểm hoặc một đường thẳng thuộc mặt trụ: + Chứng minh một điểm M thuộc mặt trụ: Chứng minh khoảng cách từ M đến đường thẳng cố định D bằng một số không đổi. + Chứng minh một đường thẳng d thuộc mặt trụ: Chứng minh d // D cố định và khoảng cách từ M bất kỳ trên d đến đường thẳng D bằng một số không đổi. O M P d D Ví dụ: Cho đường tròn (C) trong mp (P). Từ một điểm M trên (C) kẻ đường thẳng d vuông góc với mp (P). Chứng minh đường thẳng d nằm trên một mặt trụ. Giải Gọi D là đường thẳng vuông góc với mp (P) tại O Gọi r là bán kính của (C). Do Khoảng cách giữa d và D là: d(d, D) = OM = r: không đổi Vậy d nằm trên mặt trụ trụ D bán kính r Bài tập tương tự: Cho mp (P). Gọi A là một điểm nằm trên (P) và B là điểm nằm ngoài (P) sao cho hình chiếu H của B trên (P) không trùng với A. Một điểm M chạy trên mp(P) sao cho góc ABM = BMH. CMR: điểm M luôn nằm trên một mặt trụ tròn xoay có trục AB. HD: Gọi I là hình chiếu M trên AB. CM: MI có độ dài không đổi. DẠNG 2: Tính diện tích xung quanh mặt trụ và thể tích khối trụ. Ví dụ: Cho khối trụ có bán kính đáy bằng r và có thiết diện qua trục là một hình vuông. Tính diện tích xung quanh và diện tích toàn phần của hình trụ. Tính thể tích của khối lăng trụ tứ giác đều nội tiếp trong hình trụ đã cho (hình lăng trụ này có đáy là hình vuông nội tiếp trong đường tròn đáy của hình trụ) Gọi V là thể tích khối lăng trụ đều nội tiếp trong khối trụ và V’ là thể tích khối trụ. Tính tỉ số của V và V’. Giải Vì thiết diện qua trục của hình trụ là hình vuông nên đường sinh l bằng đường cao h A B C D O A’ B’ C’ D’ O’ l = h = 2r. Diện tích xung quanh của hình trụ: Sxq = 2p r l = 4p r2. Diện tích toàn phần của hình trụ: Stp = Sxq + 2B = 6p r2. Gọi ABCD.A’B’C’D’ là trụ tứ giác đều nội tiếp trong hình trụ đã cho. Ta có: ABCD nội tiếp trong đường tròn đáy nên: AB = r Thể tích khối lăng trụ tứ giác đều: V = AA’.SABCD = 4r3. c) Thể tích khối trụ: V’ = B.h = 2p r3 Vậy: BÀI TẬP Bài 1. Một hình trụ có bán kính đáy bằng 50 cm và có chiều cao h = 50 cm. Tính diện tích xung quanh và thể tích khối trụ được tạo nên. Một đoạn thẳng có chiều dài 100 cm và có hai đầu mút nằm trên hai đường tròn đáy. Tính khoảng cách từ đoạn thẳng đó đến trục của hình trụ. Bài 2. Một khối trụ có bán kính đáy bằng r và chiều cao r. Gọi A và B là hai điểm trên hai đường tròn đáy sao cho góc được tạo thành giữa đường thẳng AB và trục của khối trụ bằng 300. Tính diện tích của thiết diện qua AB và song song với trục của khối trụ. Tính độ dài đoạn vuông góc chung của AB và trục của khối trụ. Bai 3. Một hình trụ có các đáy là hai hình tròn tâm O và O’ bán kính r và có đường cao h = r. Gọi A là điểm trên đường tròn tâm O và B là điểm trên đường tròn O sao cho AO ^ O’B CMR: các mặt bên của tứ diện OABO’ là các tam giác vuông. Tính thể tích tứ diện này Gọi (P) là mặt phẳng qua AB và song song vơi OO’. Tính khoảng cách giữa OO’ và mp(P) Bài 4. Cho hình chóp tam giác đều S.ABC có SA= SB= SC = a và có góc giữa mặt bên và mặt phẳng đáy bằng a. Tính diện tích xung quanh của hình trụ có đường tròn đáy là đường tròn nội tiếp tam giác đáy của hình chóp và có chiều cao bằng chiều cao của hình chóp. Bài 5. Một hình trụ có các đáy là hai hình tròn tâm O và O’ bán kính r và có đường cao h = r . A và B là hai điểm di động trên hai đường tròn O và O’ sao cho góc (OA, O’B) không đổi. a) Tính diện tích xung quanh và diện tích toàn phần của hình trụ b) Thể tích khối trụ tương ứng. Bài 6. Cho hình chóp S.ABCD có đáy là hình vuông cạnh a và đường cao SA = 2a. MNPQ là thiết diện song song với đáy M Î SA và AM = x. Xét hình trụ có đáy là đường tròn ngoại tiếp MNPQ và đường sinh MA. Tính diện tích MNPQ theo a và x. Tính thể tích lăng trụ theo a và x. Tìm hình lăng trụ có thể tích lớn nhất. III) MẶT CẦU, HÌNH CẦU VÀ KHỐI CẦU: DẠNG 1: Xác định tâm và bán kính mặt cầu ngoại tiếp hình chóp (hình lăng trụ). * Phương pháp 1: Xác định điểm O cách đều các đỉnh của hình chóp. a S A B C D I M O Khi đó: O là tâm mặt cầu ngoại tiếp. * Phương pháp 2: + B1: Xác định đường thẳng a đi qua tâm I của đường tròn ngoại tiếp đa giác đáy. (a gọi là trục của đường tròn) + B2: Dựng đường thẳng trung trực của cạnh bên cắt a tại O. + B3: Kết luận O là tâm mặt cầu. Ví dụ 1: Cho hình lập phương ABCD.A’B’C’D’ cạnh a. Xác định tâm và bán kính mặt cầu đi qua 8 đỉnh của hình lập phương đã cho. Giải Ap dụng pp1: Gọi O là trung điểm của đường chéo AC’. Ta có: O cách đều các đỉnh của hình lập phương Vậy mặt cầu đi qua 8 đỉnh hình lập phương có tâm O, A B C D A’ B’ C’ D’ O Bán kính r = AC’ = a Þ r = Ví dụ 2: Cho tứ diện D.ABC có DA ^ (ABC) và DA = 5a, tam giác ABC vuông tại B và AB = 3a, BC = 4a. Xác định tâm và bán kính mặt cầu đi qua bốn đỉnh của tứ diện. Giải A B C D O Ap dụng pp1: Gọi O là trung điểm DC Do DA ^ (ABC) nên DA ^ AB, DA ^ AC Þ D DAC vuông tại A Þ OA = OC = OD = CD/2 (1) Ta có: BC ^ BA, BC ^ DA Þ BC ^ (ABD) Þ BC ^ BD Þ OB = CD/ 2 (2) Từ (1 và (2) suy ra: A, B, C, D thuộc mặt cầu tâm O, bán kính r = CD/2. S A B H C Ví dụ 3: Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a, cạnh bên bằng b. Xác định tâm và bán kính mặt cầu đi qua các đỉnh hình chóp. Giải Gọi H là trọng tâm tam giác ABC. Do SABC là hình chóp đều nên tâm O của mặt cầu nằm trên SH. Gọi I là trung điểm của SA. Trong mp(SAH) dựng IO vuông góc với SA cắt SH tại O Khi đó: O là tâm mặt cầu đi qua các đỉnh hình chóp. Xét hai tam giác đồng dạng SIO và SHA ta có: Þ SO = Mà SH2 = SA2 - AH2 = b2 - Nên SH = Vậy: r = = BÀI TẬP Bài 1. Cho tứ diện D.ABC có DA ^ (ABC) và DA = 4a, tam giác ABC vuông tại B và AB = 6a, BC = 8a. Xác định tâm và bán kính mặt cầu đi qua bốn đỉnh A, B, C, D của tứ diện. Bài 2. Cho hình chóp SABCD có đáy ABCD là hình vuông cạnh a, SA ^ (ABCD) và SA = 2a, Xác định tâm và bán kính mặt cầu đi qua 5 đỉnh S, A, B, C, D. Bai 3. Cho hình chóp tứ giác đều SABCD có cạnh đáy bằng a, cạnh bên bằng b. Xác định tâm và bán kính mặt cầu đi qua 5 đỉnh S, A, B, C, D. Bài 4. Cho tứ diện OABC có góc AOB = 900, COB = 600, AOC = 1200, OA= OB= OC = a Có nhận xét gì về tam giác ABC? Xác định hình chiếu vuông góc của O trên mp(ABC) Xac định tâm và bán kính mặt cầu đi qua 4 đỉnh O, A, B, C. Bài 5. Cho tứ diện đều SABC có cạnh đáy bằng a. Gọi H là hình chiếu của S trên (ABC). CM: H là tâm đường tròn ngoại tiếp tam giác ABC Xác định và bán kính mặt cầu đi qua 4 đỉnh S, A, B, C. Gọi I là trung điểm SH. CMR: IA, IB, IC đôi một vuông góc. Bai 6. Cho tứ diện SABC có SA = a và SA vuông góc với mp(ABC), AB = AC = b, góc BAC= 600. Xac định tâm và bán kính mặt cầu đi qua 4 đỉnh S, A, B, C. Bài 7. Cho hình chóp tứ giác đều SABCD có cạnh đáy bằng a, chiều cao bằng 2a. Xác định tâm và bán kính mặt cầu đi qua 5 đỉnh S, A, B, C, D Bài 8. Cho hình chóp tứ giác đều SABCD có cạnh đáy bằng a, cạnh bên hợp với đáy một góc 600. Xác định tâm và bán kính mặt cầu đi qua 5 đỉnh S, A, B, C, D. Bài 9. Cho hình vuông ABCD tâm O, cạnh a. Trên đường thẳng vuông góc với mp(ABCD) tại O lấy điểm S sao cho SO = . Xác định tâm và bán kính mặt cầu đi qua 5 đỉnh S, A, B, C, D. DẠNG 2: Xét vị trí tương đối của mặt cầu S(O, r) và mặt phẳng (P): Phương pháp: Xác định khoảng cách d từ O đến mp(P). * Nếu d > r: (P) không cắt (S) * Nếu d = r: (P) tiếp xúc (S) * Nếu d < r: (P) cắt (S) theo đường tròn có bán kính r’ = Đặc biệt nếu d = 0 thì (P) cắt (S) theo đường tròn lớn. DẠNG 3: Xét vị trí tương đối của mặt cầu S(O, r) và đường thẳng a: Phương pháp: Xác định khoảng cách d từ O đến đường thẳng a. * Nếu d > r: a không cắt (S) * Nếu d = r: a tiếp xúc (S) * Nếu d < r: a cắt (S) tại hai điểm phân biệt Ví dụ: Cho mặt cầu S(O,r) và một điểm a biết OA = 2r. Qua A kẻ một tiếp tuyến với mặt cầu tại B và kẻ một cát tuyến cắt mặt cầu tại C và D. Cho biết CD = r Tính AB Tính khoảng cách từ O đến CD. Giải A O C D B H a) Ta có: AB là tiếp tuyến của mặt cầu tại B nên AB ^ OB Þ AB = b) Gọi H là hình chiếu vuông góc của O trên CD. Ta có: OC = OD = r Nên tam giác OCD cân tại O Do H là trung điểm của CD nên HC = Vậy khoảng cách từ O đến CD là độ dài OH với OH = Bài tập: Cho mặt cầu S(O, r) tiếp xúc với mp(P) tại I. Gọi M là điểm nằm trên mặt cầu nhưng không phải là điểm đối xứng của I qua O. Từ M kể hai tiếp tuyến của mặt cầu vuông góc với nhau lần lượt cắt mặt phẳng (P) tại A và B. CMR: AB2 = AI2 + IB2. DẠNG 4: Diện tích mặt cầu, thể tích khối cầu: S = 4p r2, V = p r3. Ví dụ: Cho tứ diện ABCD có DA = 5a và DA vuông góc với mp(ABC). Tam giác ABC vuông tại B và AB = 3a, BC = 4a. Xác định tâm và bán kính của mặt cầu đi qua các đỉnh của tứ diện. A B C D O Tính diện tích mặt cầu và thể tích của khối cầu tương ứng. Giải a) Gọi O là trung điểm DC Do DA ^ (ABC) nên DA ^ AB, DA ^ AC Þ D DAC vuông tại A Þ OA = OC = OD = CD/2 (1) Ta có: BC ^ BA, BC ^ DA Þ BC ^ (ABD) Þ BC ^ BD Þ OB = CD/ 2 (2) Từ (1 và (2) suy ra: A, B, C, D thuộc mặt cầu tâm O, bán kính r = CD/2. r = = b) Diện tích mặt cầu: S = 4p r2 = 50p a2 Thể tích của khối cầu tương ứng: V = p r3 = BÀI TẬP Bài 1. Cho hình lăng trụ ABC.A’B’C’ có tất cả các cạnh đều bằng a. Xác định tâm và bán kính mặt cầu đi qua các đỉnh của lăng trụ. Tính diện tích mặt cầu và thể tích của khối cầu tương ứng Bài 2. Cho hình chóp SABCD có đáy là hình vuông cạnh a, SA ^ (ABCD). Dựng mp(P) qua A và vuông góc với SC. Mặt phẳng (P) cắt SB, SC, SD tại B’, C’, D’. CMR: 7 điểm A, B, C, D, A’, B’ C’, D’ luôn nằm trên một mặt cầu Tính diện tích mặt cầu và thể tích của khối cầu được tạo thành. Bài 3. Cho hình chóp tam giác đều SABC có cạnh đáy bằng a, mặt bên hợp với đáy một góc bằng 600. Xác định tâm và bán kính mặt cầu đi qua các đỉnh của lăng trụ. Tính diện tích mặt cầu và thể tích của khối cầu tương ứng. Bài 4. Cho hình chóp SABC có SA = SB = SC = a và có chiều cao h. Xác định tâm và bán kính mặt cầu đi qua các đỉnh của lăng trụ. Tính diện tích mặt cầu đó.
Tài liệu đính kèm:
 CD_Hinh_Hoc_Ch1+2.doc
CD_Hinh_Hoc_Ch1+2.doc





