Chuyên đề Hai quy tắc đếm cơ bản
Hai quy tắc đếm cơ bản
A. Tóm tắt lý thuyết
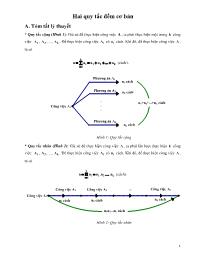
* Quy tắc cộng (Hình 1): Giả sử để thực hiện công việc A , ta phải thực hiện một trong k công
việc: A1 , A2 , ., Ak . Để thực hiện công việc Ai có ni cách. Khi đó, để thực hiện công việc A ,ta có
Bạn đang xem tài liệu "Chuyên đề Hai quy tắc đếm cơ bản", để tải tài liệu gốc về máy bạn click vào nút DOWNLOAD ở trên
1 Hai quy tắc đếm cơ bản A. Tóm tắt lý thuyết * Quy tắc cộng (Hình 1): Giả sử để thực hiện công việc A , ta phải thực hiện một trong k công việc: 1A , 2A , ..., kA . Để thực hiện công việc iA có in cách. Khi đó, để thực hiện công việc A , ta có k i 1 2 k i 1 n n n n n (cách). nk cách . . . Phương án Ak Phương án A2 n1+n2+...+nk cách n2 cách n1 cách Phương án A1 Công việc A: Hình 1: Quy tắc cộng * Quy tắc nhân (Hình 2): Giả sử để thực hiện công việc A , ta phải lần lượt thực hiện k công việc: 1A , 2A , ..., kA . Để thực hiện công việc iA có in cách. Khi đó, để thực hiện công việc A , ta có k i 1 2 ki 1 n n n . .n .n (cách). n1n2...nk cách nk cáchn2 cáchn1 cách ... Công việc AkCông việc A2Công việc A1 Công việc A: Hình 2: Quy tắc nhân 2 B. Một số ví dụ Ví dụ 1. Có thể lập được bao nhiêu số có năm chữ số đôi một khác nhau từ các chữ số từ 0 đến 9 . Giải Giả sử số cần lập là 1 2 5A a a ...a . Để lập số A , ta phải lần lượt chọn 1a , 2a , ..., 5a sao cho 1a 0 và 1a , 2a , ..., 5a đôi một khác nhau. +) 1a 0 có 9 cách chọn 1a . +) 2a có thể bằng 0 , tuy nhiên 2 1a a có 9 cách chọn 2a . +) lập luận hoàn toàn tương tự, ta có số cách chọn 3a , 4a , 5a lần lượt là: 8 , 7 , 6 cách. Vậy theo quy tắc nhân thì số cách lập số A là 9.9.8.7.6 27216 cách. Ví dụ 2. Có thể lập được bao nhiêu số có năm chữ số đôi một khác nhau chia hết cho 5 từ các chữ số từ 0 đến 9 . Giải Giả sử số cần lập là 1 2 5A a a ...a . Để lập số A ta có hai phương án như sau: +) Phương án 1: Chọn 1a 5 5a 0 , số cách chọn 2a , 3a , 4a lần lượt là: 8 , 7 , 6 cách. Do đó, theo quy tắc nhân thì phương án này có số cách thực hiện là: 8.7.6 336 cách 1 . +) Phương án 2: Chọn 1a 5 có 8 cách chọn 1a , 2 cách chọn 5a , cũng tương tự như phương án 1 số cách chọn 2a , 3a , 4a lần lượt là: 8 , 7 , 6 cách. Do đó, theo quy tắc nhân thì phương án này có số cách thực hiện là: 8.2.8.7.6 5376 cách 2 . Từ 1 , 2 , áp dụng quy tắc cộng ta có số cách lập số A là 336 5376 5712 cách. Nhận xét: Việc lập số A trong Ví dụ 2 được chia thành hai phương án vì việc 1a có bằng 5 hay khác 5 có ảnh hưởng đến số cách chọn 5a . Ví dụ 3. Có thể lập được bao nhiêu số có năm chữ số đôi một khác nhau từ các chữ số từ 0 đến 9 biết rằng số này có đúng hai chữ số 1 và các chữ số còn lại đôi một khác nhau. Giải Giả sử số cần lập là 1 2 5A a a ...a . Để lập số A ta có hai phương án như sau (về cách chọn 1a ): +) Phương án 1: 1a 1 chọn thêm một vị trí nữa cho cho chữ số 1 có 4 cách, lần lượt chọn chữ số cho ba vị còn lại có số cách lần lượt là: 9 , 8 , 7 cách. Do đó, số cách lập số A theo phương án này là 1.4.9.8.7 2016 cách. 3 +) Phương án 2: 1a 1 có 8 cách chọn 1a , có 6 cách chọn hai vị trí cho chữ số 1 , lần lượt chọn chữ số cho hai vị còn lại có số cách lần lượt là: 8 , 7 cách. Do đó, số cách lập số A theo phương án này là 8.6.8.7 2688 cách. Vậy số cách lập số A là 2016 2688 4704 cách. Ví dụ 4. Từ các chữ số 0 , 1 , 2 , 3 , 4 , 5 có thể lập được bao nhiêu số tự nhiên mà mỗi số có 6 chữ số đôi một khác nhau và chữ số 2 đứng cạnh chữ số 3 . Giải Giả sử số cần lập là 1 2 5A a a ...a . Để lập số A ta có hai phương án như sau: +) Phương án 1: xếp 2 và 3 vào hai vị trí đầu tiên có 1n 2 cách ( 1a 2 , 2a 3 hoặc ngược lại). Lần lượt chọn chữ số cho các vị trí 3a , 4a , 5a , 6a số cách chọn lần lượt là 2n 4 , 3n 3 , 4n 2 , 5n 1 . +) Phương án 2: xếp 2 và 3 vào hai vị trí, tránh vị trí 1a có thể xếp 2 và 3 vào các vị trí: 2a và 3a , 3a và 4a , 4a và 5a , 5a và 6a số cách xếp 2 và 3 theo phương án này là: 1m 2.4 8 cách. Số cách chọn 1a là 2m 3 . Lần lượt chọn chữ số cho 3 vị trí còn lại số cách chọn lần lượt là 3m 3 , 4m 2 , 5m 1 . Vậy số các số thỏa mãn yêu cầu bài toán là: 1 2 3 4 5 1 2 3 4 5n n n n n m m m m m 2.4.3.2.1 8.3.3.2.1 192 . Ví dụ 5. Có 6 quả cầu xanh được đánh số từ 1 đến 6 , 5 quả cầu đỏ được đánh số từ 1 đến 5 và 4 quả cầu vàng được đánh số từ 1 đến 4 . Hỏi có bao nhiêu cách chọn ra 3 quả cầu vừa khác mầu vừa khác số. Giải Để chọn được 3 quả cầu thỏa mãn yêu cầu bài toán, ta lần lượt làm như sau: Bước 1: Chọn quả cầu vàng có 1n 4 cách. Bước 2: Chọn quả cầu đỏ: vì không được chọn quả cầu đỏ có số trùng với số của quả cầu vàng đã chọn ở bước 1 số cách chọn quả cầu đỏ là 2n 4 . Bước 3: Chọn quả cầu xanh: vì không được chọn quả cầu xanh có số trùng với số của các quả cầu đã chọn ở bước 1 và bước số cách chọn quả cầu đỏ là 3n 4 . Vậy số cách chọn ra 3 quả cầu vừa khác mầu vừa khác số là: 1 2 3n .n .n 64 . 4 C. Bài tập Bài 1. Giả sử bạn muốn mua áo sơ mi cỡ 39 hoặc 40. Áo cỡ 39 có 5 màu khác nhau, áo cỡ 40 có 4 màu khác nhau. Hỏi 1) Có bao nhiêu sự lựa chọn một chiếc áo? 2) Có bao nhiêu sự lựa chọn hai chiếc áo khác cỡ? Bài 2. Giả sử bạn muốn mua áo sơ mi cỡ 39 hoặc 40. Áo cỡ 39 có 4 màu là trắng, xanh, đỏ, vàng; áo cỡ 40 có 3 màu là trắng, đỏ, tím. Hỏi 1) Có bao nhiêu sự lựa chọn một chiếc áo? 2) Có bao nhiêu sự lựa chọn hai chiếc áo khác cỡ? 3) Có bao nhiêu sự lựa chọn hai chiếc áo khác màu? 4) Có bao nhiêu sự lựa chọn hai chiếc áo khác cả cỡ và màu? Bài 3. Có bao nhiêu số tự nhiên có năm chữ số sao cho 3 chữ số đầu tiên khác nhau và các chữ số cách đều chữ số đứng giữa thì giống nhau. Bài 4. Từ cách chữ số 1 , 5 , 6 , 7 có thể lập được bao nhiêu số tự nhiên 1) Có bốn chữ số. 2) Có bốn chữ số đôi một khác nhau. Bài 5. Từ các chữ số 1 , 5 , 6 , 7 có thể lập được bao nhiêu số tự nhiên lớn hơn 4000 có 4 chữ số nếu 1) Các chữ số không nhất thiết khác nhau. 2) Các chữ số đôi một khác nhau. Bài 6. Có bao nhiêu số có 3 chữ số được tạo thành từ các chữ số 2 , 3 , 4 , 5 , 6 nếu 1) Các chữ số của nó không nhất thiết khác nhau. 2) Các chữ số của nó đôi một khác nhau. 3) Các chữ số của nó hoàn toàn giống nhau. Bài 7. Từ cách chữ số 0 , 1 , 2 , 3 , 4 , 5 có thể lập được bao nhiêu số tự nhiên 1) Có bốn chữ số. 2) Có bốn chữ cố đôi một khác nhau. 3) Có bốn chữ số đôi một khác nhau và chia hết cho 5. Bài 8. Có bao nhiêu số tự nhiên lẻ trong khoảng 2000;3000 có thể tạo nên bằng các chữ số 1 , 2 , 3 , 4 , 5 , 6 nếu 1) Các chữ số của nó không nhất thiết khác nhau. 2) Các chữ số của nó đôi một khác nhau. 5 Bài 9. Khi gieo đồng thời ba con súc sắc có bao nhiêu khả năng mà tổng số chấm xuất hiện trên ba mặt của ba con súc sắc là 9 (giả thiết vai trò của ba con súc sắc khác nhau). Bài 10. Có 4 hành khách bước lên một đoàn tàu có 4 toa. Hỏi 1) Có bao nhiêu trường hợp có thể xảy ra về cách chọn toa của 4 hành khách. 2) Có bao nhiêu trường hợp mà mỗi toa có 1 người lên. 3) Có bao nhiêu trường hợp mà một toa có 3 người lên, một toa có 1 người lên và hai toa còn lại không có ai lên. 6 D. Hướng dẫn giải Bài 1. 1) Để chọn một áo, ta có thể chọn áo cỡ 39 hoặc áo cỡ 40. Chọn áo cỡ 39 có 5 cách, chọn áo cỡ 40 có 4 cách có 5 4 9 cách chọn một áo. 2) Cách 1: Để chọn hai áo khác cỡ, ta phải chọn một chiếc cỡ 39 và một chiếc cỡ 40. Chọn áo cỡ 39 có 5 cách, chọn áo cỡ 40 có 4 cách có 5.4 20 cách chọn hai áo khác cỡ. Cách 2: (Giải bài toán ngược) Chọn hai áo khác nhau có 9.828 7 ... 1 36 cách, chọn hai áo khác nhau cùng cỡ có 4 3 2 1 3 2 1 16 cách có 36 16 20 cách chọn hai áo khác cỡ.
Tài liệu đính kèm:
 CD1_HaiQuyTac.pdf
CD1_HaiQuyTac.pdf





