Các đề thi Tích phân
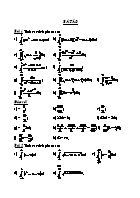
CÁC PHƯƠNG PHÁP TÍNH TÍCH PHÂN
I. Phương pháp đổi biến số
Thông thường, người ta dùng phương pháp đổi biến số khi gặp tích phân có dạng sau: Khi hàm số dưới dấu tích phân f(x) có thể phân tích thành tích của một hàm số hợp g[(x)] và đạo hàm của hàm số ở bên trong(x) tức là f(x) = g[(x)].(x). Khi đó, để tính:
Bạn đang xem tài liệu "Các đề thi Tích phân", để tải tài liệu gốc về máy bạn click vào nút DOWNLOAD ở trên
BÀI TẬP Bài 1. Tính các tích phân sau: a) ; b) ; c) ; d) ; e) ; f) ; g) ; h) ; i) ; j) ; k) . Đáp số : a) – ; b); c); d) – ; e) 8ln3 – 6; f) 2ln2 – ln3; g) – ln2; h); i) ; j) ; k) 28 – 4e. Bài 2. Tính các tích phân sau: a) ; b) ; c) ; d) ; e) . Đáp số : a) 1; b) ; c) ; d) ; e) 1 + ; Bài 3. Tính các tích phân sau: a) ; b) ; c) ; d) ; e); f) ; g) h) ; i) . Đáp số : a) ; b); c) 1 – ; d) ; e) –+ 2; f) – ; g) ; h) 3 – ; i) . Bài 3. Chứng minh rằng a) ; b) ; c) ; d) . CÁC PHƯƠNG PHÁP TÍNH TÍCH PHÂN I. PHƯƠNG PHÁP ĐỔI BIẾN SỐ Thông thường, người ta dùng phương pháp đổi biến số khi gặp tích phân có dạng sau: Khi hàm số dưới dấu tích phân f(x) có thể phân tích thành tích của một hàm số hợp g[(x)] và đạo hàm của hàm số ở bên trong’(x) tức là f(x) = g[(x)].’(x). Khi đó, để tính: ta thực hiện phép đổi biến số t = (x) và ta có = (*) Trong đó, và được xác định bởi = (a) và = (b). Chú ý: Khi sử dụng công thức đổi biến số (*) thì phải nhớ rằng: Khi đã đổi biến số lấy tích phân từ x sang t đồng thời ta cũng phải đổi luôn cận lấy tích phân từ a, b sang , và ta tính toán với những cận mới ấy, không cần phải quay lại biến số cũ x như trong tích phân bất định. BÀI TẬP Tính các tích phân sau: 1) ; 2) ; 3) ; 4) ; 5) ; 6) ; 7) ; 8) ; 9) ; 10) ; 11) ; 12) ; 13) ; 14) ; 15) ; 16) ; 17) ; 18) ; 19) ; 20) ; 21) ; 22); 23) ; 24) ; 25) 26) ; 27) ; 28) ; 29) ; 30) ; 31) ; 32) ; 33) ; 34) ; 35) ; 36) ; 37) ; 38) ; 39) ; 40) ; 41) ; 42) ; 43) ; 44) 45); 46) ; 47) ; 48) ; 49) ; 50) ; 51) ; 52) ; 53) ; 54) ; 55) ; 56) ; 57) ; 58) ; 59) ; 60) ; Đáp số : 1) ; 2) ; 3) ; 4) 4 + 8ln; 5) ; 6) ln3; 7) – 4; 8) ; 9) ; 10) ; 11) ; 12) ; 13) ; 14) ; 15) ; 16) ; 17) ln2; 18) ln2; 19) ln2; 20) ; 21) ; 22) + ln2 – 1; 23); ; 24) ; 25) ln2; 26) 2; 27) 2; 28) ; 29) ln2; 30) ; 31) ; 32) ; 33) ; 34) e – ; 35) ; 36) ; 37) 2e(e – 1); 38) ; 39); 40) 1 + 2arctge – 41) ; 42); 43)1 – cos1; 44) 45) ln2; 46) ; 47) ; 48) ; 49) ; 50); 51) ; 52) ; 53) ; 54) ; 55) ; 56) 57) ; 58) ; 59) 1; 60) ln2; * Vài đề thi 1) (A, 2005) Đ.S: ; 2) (B, 2005) Đ.S: ; 3) (D, 2005) Đ.S: ; 4) (TN, 2005) Đ.S: . 5) (CĐKTĐN, 2005) I = . () 6) (CĐKTCN, 2005) () II. PHƯƠNG PHÁP TÍCH PHÂN TỪNG PHẦN Định lý: Nếu u, v là hai hàm số có đạo hàm liên tục trên đoạn [a; b] thì : . Nhận xét : Vì v’(x)dx = dv và u’(x)dx = du nên công thức trên có thể viết gọn là Tích phân dạng , trong đó Pn(x) là đa thức bậc n theo biến x Phương pháp : Đặt Chú ý: Ta phải tính tích phân từng phần theo n lần. BÀI TẬP Tính các tích phân sau 1) ; 2) ; 3) ; 4) ; 5) . Đáp số: 1) 1; 2) e; 3) 4) ; 5) . Tích phân dạng I1 = . Phương pháp : * Để tính I1 ta đặt : * Để tính I2 ta đặt : Bài tập: Tính các tích phân sau: 1) ; 2) ; 3) ; 4) ; 5) ; 6) ; 7) ; 8) ; 9) . Đáp số: 1) 1; 2) ; 3) ; 4) ; 5) ; 6) ; 7) ; 8) 3 – 6; 9) . Tích phân dạng I = . Phương pháp : Đặt Ta tính tích phân từng phần n lần. BÀI TẬP Tính các tích phân sau: 1) ; 2) ; 3) ; 4) ; 5) ; 6) ; 7) ; 8) ; 9) ; 10) ; 11) ; 12) ; Đáp số: 1) 1; 2) 4; 3) 48ln2 – ; 4) e – 2; 5) ; 6) 2 – ; 7) ; 8) ; 9) 3ln; 10) ; 11) 2ln( – 2) + –1; 12) ; * Khối D, 2004) Tính tích phân I = . Đáp số : I = 3ln3 – 2. Tích phân dạng Đặt (Hoặc đặt ngược lại) Ta lấy tích phân từng phần hai lần rồi giải phương trình. BÀI TẬP Tính các tích phân sau: 1) ; 2) ; 3) ; 4) ; 5) ; 6) ; 7) ; 8) ; 9) . Đáp số: 1) ; 2) – ; 3) ; 4) ; 5) ; 6)(sin1 + cos1 –1) 7) + e + ; 8) ; 9). MỘTSỐ ĐỀ THI I. CÁC ĐỀ THI TỐT NGHIỆP. Tính các tích phân sau: TN, 1994 (2 điểm) 1) ; 2) . ĐS: 1) ; 2) . TN, 1996 (2 điểm) 1) 2) . ĐS: 1) ; 2) . TN, 1997, đợt 1 (2 điểm) 1) 2) . ĐS: 1) 18ln3 - 8ln2 - 5 ; 2) . TN, 1997, đợt 2 1) . ĐS: TN, 1998, Đề chính thức (2 điểm) 1) 2) . ĐS. 1) - 2; 2) . TN, 1998, đợt 1 (2 điểm) 1) . ĐS: . TN, 1998, đợt 2 (2 điểm) 1) . ĐS: . TN, 1999, đợt 1 (2 điểm) ; ĐS: TN, 1999, đợt 2 (2 điểm) Tính tích phân (ĐS: ). Giải phương trình . TN, 2000 Cho hàm số . Hãy tính đạo hàm và giải phương trình ; Có 5 tem thư khác nhau và 5 bì thư cũng khác nhau. Người ta muốn chọn từ đó ra 3 tem thư, 3 bì thư và dán 3 tem thư ấy lên 3 bì thư đã chọn. Mỗi bì thư chỉ dán một tem thư. Hỏi có bao nhiêu cách làm như vậy. TN, 2000 - 2001 (1 điểm) Tính tích phân (ĐS: ). TN, 2001 - 2002 (2 điểm) Tìm giá trị nhỏ nhất và giá trị lớn nhất của hàm số F(x) = cos2x + 4sinx trên đoạn . Có bao nhiêu số tự nhiên chẵn có bốn chữ số đôi một khác nhau? TN, 2002 - 2003 (2 điểm) Tìm nguyên hàm của hàm của hàm số Biết rằng Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số và đường thẳng Đáp số. 1) 2) (TN 2003 – 2004) Tính thể tích của vật thể tròn xoay do hình phẳng giới hạn của đồ thị hàm số và các đường quay quanh trục ĐS. (TN, 2005) Đ.S: . TN không phân ban, 2006) Tính diện tích hình phẳng giới hạn bởi các đồ thị hàm số và đường thẳng Tính tích phân Đáp số. 1) 2) (TN 2006, Ban KHTN) ĐS. (TN 2006, Ban KHXH) ĐS. (TN không phân ban, 2007) ĐS. (TN ban KHTN, lần 1, 2007) ĐS. (TN ban KHXH, lần 1, 2007) ĐS. (TN không phân ban, 2007) ĐS. (TN ban KHTN, lần 2, 2007) Cho hình giới hạn bởi các đường Tính thể tích khối tròn xoay được tạo thành khi quay hình quanh trục hoành. ĐS. (TN ban KHTN, lần 2, 2007) Tính diện tích hình phẳng giới hạn bởi các đường và ĐS. 36 (đ.v.d.t.) II. CÁC ĐỀ THI ĐẠI HỌC, CAO ĐẲNG (Khối A, 2002) Tìm diện tích hình phẳng giới hạn bởi các đường Đáp số. (Khối B, 2002) Tìm diện tích hình phẳng giới hạn bởi các đường Đáp số. Tính các tích phân sau: (Dự bị 1, 2002) (Đáp số: ). (Dự bị 2, 2002) (Đáp số. - 1) (Dự bị 4, 2002) (Đáp số. ). (Dự bị 5, 2002) Đáp số: ). (Khối A, 2003) (Đáp số: ). (Khối A, Dự bị 1, 2003) (Đáp số: ) (Khối A, Dự bị 2, 2003) (Đáp số: ). (Khối B, 2003) (Đáp số: ). (Khối B, Dự bị 1, 2003) (Đáp số: ). (Khối B, Dự bị 2, 2003) Cho hàm số . Tìm a và b sao cho và Đáp số: (Khối D, 2003) ĐS. 1. (Dự bị 1, Khối D, 2003) ĐS. (Dự bị 2, Khối D, 2003) ĐS. (Khối B, 2004) (Đáp số: ). (Khối A, 2004) (Đáp số: ). (Khối D, 2004) (Đáp số: 3ln3 - 2). (Dự bị 1, 2004) ĐS. 2. (Dự bị 2, 2004) ĐS. (Dự bị 3, 2004) ĐS. (Dự bị 4, 2004) ĐS. (Dự bị 5, 2004) ĐS. (A, 2005) Đ.S: (B, 2005) Đ.S: . (D, 2005) Đ.S: . (Dự bị 1, 2005) ĐS. (Dự bị 2, 2005) ĐS. (Dự bị 3, 2005) ĐS. (Dự bị 4, 2005) ĐS. (Dự bị 5, 2005) ĐS. (A, 2006) ĐS. . (B, 2006) ĐS. . (D, 2006) ĐS. (Dự bị 1, A, 2006) ĐS. (Dự bị 2, A, 2006) Tính diện tích hình phẳng giới hạn bởi parabol và đường thẳng ĐS. (Dự bị 1, D, 2006) ĐS. (Dự bị 2, D, 2006) ĐS. (Dự bị 1, B, 2006) ĐS. (Dự bị 2, B, 2006) ĐS. (D, 2007) ĐS. (A, 2007) Tính diện tích hình phẳng giới hạn bởi hai đường ĐS. (Khối B, 2007) ĐS.
Tài liệu đính kèm:
 cac de thi tich phan.doc
cac de thi tich phan.doc





