Chyên đề Hình chóp: góc – khoảng cách
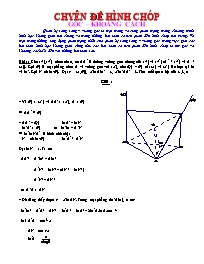
Quan hệ song song – vuông góc là một mảng vô cùng quan trọng trong chương trình hình học không gian nói chung và trong những bài toán có liên quan đến hình chóp nói riêng. Và một trong những ứng dụng quan trọng nhất của quan hệ song song – vuông góc trong việc giải các bài toán hình học không gian cũng như các bài toán có liên quan đến hình chóp là tìm góc và khoảng cách.Ta đến với những bài toán sau:
Bạn đang xem 20 trang mẫu của tài liệu "Chyên đề Hình chóp: góc – khoảng cách", để tải tài liệu gốc về máy bạn click vào nút DOWNLOAD ở trên
CHYÊN ĐỀ HÌNH CHÓP GÓC – KHOẢNG CÁCH Quan hệ song song – vuông góc là một mảng vô cùng quan trọng trong chương trình hình học không gian nói chung và trong những bài toán có liên quan đến hình chóp nói riêng. Và một trong những ứng dụng quan trọng nhất của quan hệ song song – vuông góc trong việc giải các bài toán hình học không gian cũng như các bài toán có liên quan đến hình chóp là tìm góc và khoảng cách.Ta đến với những bài toán sau: Bài 1: Cho (D),(D¢) chéo nhau, có AA¢ là đường vuông góc chung của (D) và (D¢) (A¢ Î (D¢) và A Î (D)). Gọi (P) là mặt phẳng chứa A và vuông góc với (D¢), còn (Q) // (P) cắt (D) và (D¢) lần lượt tại M và M¢. Gọi N=ch M/(P). Đặt g = (D,(P)), ÐMAM¢ = a, ÐM¢AA¢ = b. Tìm mối quan hệ của a,b,g. Giải : * Vì (P) ^ (D¢) và AA¢ ^ (D¢), A Î (P) Þ AA¢ Ì (P) * AA¢ // (Q) MA¢ // MN M¢A¢ ^ (P) Þ M¢M // A¢N Þ M¢MNA¢ là hình chữ nhật N = ch M/(P) M¢A¢ ^ A¢N Đặt MN = x. Ta có AA¢2 = A¢M2 – AM2 = A¢N2 + MN2 – (AN2 + MN2) = A¢N2 – AN2 Þ A¢A ^ AN * Dễ dàng thấy được g = ÐMAN. Trong mặt phẳng (M¢AM), ta có: M¢M2 = A¢A2 + AN2 = M¢A2 + MA2 – 2M¢A.MA.cos a Mà A¢A = cot b.x AN = cot g.x M¢A = MA = Þ x2(cot2b + cot2g) = x2 Û cot2b + cot2g = 2 + cot2b + cot2g - Û cos a = sin b.sin Bài 2: Cho tứ diện vuông S.ABC. M là một điểm bất thuộc DABC, I là trung điểm AB. Giả sử CA = 2SB, CB = 2SA. Kẻ SE ^ CA, SF ^ CB. CMR: a. SC ^ EF b. Giải : * Ta có SC2 = BC2 – SB2 = 4SA2 – SB2 SC2 = AC2 – SA2 = 4SB2 – SA2 Þ SA = SB Þ AC = AB * SE = SF = Þ SE = SF Từ đây ta dễ dàng suy ra: EF // AB mà SC ^ (SAB) nên EF ^ SC * Ta có : Mặt khác: AB = .SA (do DSAB vuông cân) = AC ÞEF = Lại có: Þ ÐSAC = Þ CS = = = Do đó: EF = = Þ (1) * tan SCI = tan SCA = Þ (2) * Từ (1),(2) suy ra: (đpcm) Bài 3: Trong (P) cho ABCD là hình vuông cạnh a. Lấy M,N Î CB và CD. Đặt CM = x, CN = y. Trên At ^ (ABCD) lấy S. Tìm x,y để: a. ((SAM),(SAN)) = b. ((SAM),(SMN)) = Giải : a. AM ^ SA, AN ^ SA Þ ÐMAN = ((SAM),(SAN)) SA = (SAM) Ç (SAN) Để ((SAM),(SAN)) = thì ta có: cos MAN = Û = a2 + (a – x)2 + a2 + (a – y)2 – (x2 + y2) Û 2[a2 + (a – x)2].[a2 + (a – y)2] = [4a2 – 2a(x + y)]2 Û a4 + a2[2a2 – 2a(x + y) + x2 + y2] + (a2 + x2 – 2ax)(a2 + y2 – 2ay) = 2[2a2 – a(x + y)]2. Û a4 + 2a4 – 2a3(x + y) + a4 + a2(x2 + y2) + 4a2xy – 2a3(x + y) + x2y2 – 2axy(x + y) = 8a4 – 8a3(x + y) + 2a2(x2 + y2) + 4a2xy Û x2y2 + 4a3(x + y) = 2axy(x + y) +4a4 b. Giả sử (SAM) ^ (SMN) Dựng NM¢ ^ SM ( M¢ Î SM). Ta có : Þ NM¢ ^ SA Mặt khác: SA ^ (ABCD) Þ SA ^ NM Do đó: M º M¢ Þ MN ^ (SAM) Þ MN ^ AM Vậy để (SAM) ^ (SMN) thì ta phải có: AM2 + MN2 = AN2 Û a2 + (a – x)2 + x2 + y2 = a2 + (a – y)2 Û 2x2 = 2ax – 2ay Û x2 = a(x – y). Bài 4: Cho hình chóp S.ABCD có SA ^ (ABCD) và SA = a. ABCD là hình thang vuông tại A, D. AB = 2a, AD = CD = a a. Tính góc (S, BC, A) và (A, BS, C) b. Tính góc ((SBC),(SCD)) Giải : * Xét mp (ABCD) + Gọi H = ch C/AB Þ AHCD là hình vuông, DCHB là tam giác vuông cân. Þ ÐCAB = hay CA ^ CB Từ giả thuyết ta dễ dàng có được: SB = a, BC = AC = a, SD = a Þ SC = 2a Þ SC2 + BC2 = SB2. Þ SC ^ CB Do đó: (S, BC, A) = ÐSCA = . + Gọi K = ch A/SB I = ch A/SC Þ AI ^ BC mà AI ^ SC Þ AI ^ (SBC) Þ AI ^ SB Þ SB ^ (AIK) AK ^ SB Þ KI ^ SB Þ (A, SB, C) = ÐAKI Dễ thấy:AI = a AK = Þ AI2 + KI2 = a2 + = = AK2 Þ DAKI vuông tại I Þ sin AKI = Þ ÐAKI = * Trong mp (SCD) dựng đường thẳng qua C vuông góc với SC và cắt SD tại E. Þ = ÐECB + SE.SD = SC2 Þ SE = = Þ DE = a Þ CE2 = DE.SE = + Þ BE2 = SE2 + SB2 – 2.SE.SB.cos ESB = a2 + 6a2 – 2. Þ cos ECB = = Þ ÐECB = arccos Bài 5: Cho DSAB đều và hình vuông ABCD cạnh a nằm trong 2 mặt phẳng vuông góc với nhau. Gọi M là trung điểm của AD a. Tìm d(SA,MC) b. Gọi (P) là mặt phẳng qua BC và một điểm P bất kì trên SD. Xác định giá trị lớn nhất có thể có của góc nhị diện giữa (P) và (ABCD), biết thiết diện giữa (P) và hình chóp là hình thang Giải : Gọi O là trung điểm của AB Þ SO ^ AB Mà (SAB) Ç (ABCD) = AB Þ SO ^ (ABCD) Þ SO ^ BC mà BC ^ AB Þ BC ^ (SAB) a. Gọi E là trung điểm của BC Þ AE = MC = SE = AM = EC = Þ AMCE là hình bình hành Þ MC // AE Þ Ð(MC,SA) = Ð(AE,SA) Þ cos (MC,SA) = = Þ sin (MC,SA) = . Dễ thấy SO = Ta có: VS.AMC = SO.SAMC = SO.DC.MA = = Mặt khác: VS.AMC = SA.MC.sin (MC,SA).d(SA,MC) Û = Û d(SA,MC) = b. + Thiết diện giữa (P) và hình chóp là hình thang. Dựng PQ // AD (Q Î SA) Þ PQ // BC Dễ thấy PQBC là thiết diện của (P) với hình chóp S.ABCD + Trong mặt phẳng (SAB) dựng QQ¢ // SO Þ QQ¢ ^ (ABCD) Dựng PP¢ ^ (ABCD) (P¢ Î (ABCD)) Þ (P¢Q¢BC) = ch (PQBC)/(ABCD) + Ta có: (OAD) = ch (SAD)/(ABCD) Þ P¢ Î OD, Q¢ Î OA + Đặt SP = x (0 £ x £ SD = Þ Þ Þ OP¢ = Þ Þ P¢Q¢ ^ AB Þ P¢Q¢ = Þ SP’Q’BC = .Q¢B.(P¢Q¢ + BC) = = + Þ PQ = + Þ QQ¢ = Do QQ¢ ^ Q¢B Þ QB = = = Þ SPQBC = Þ cos ((P),(ABCD)) = Đặt f(x) = "x Î [o;a] Xét f¢(x) = > 0 "x Î [o;a] Vậy max f(x) = 2 min f(x) = 1 Bài 6: Cho hình chóp tam giác S.ABC đều có đáy là tam giác đều cạnh a. Gọi là góc giữa mặt bên và mặt đáy và là góc giữa hai mặt bên. Tìm mối quan hệ giữa và . Giải: + Gọi I là trung điểm của BC . + Dựng BJ SA (). Ta dễ dàng suy ra: Suy ra: + (BJC) SA ( Do BJ = JC mà I trung điểm BC nên ) + Gọi H = ch H là tâm của ++ Bài 7: Cho hình chóp tứ giác đều có đáy là hình vuông ABCD cạnh a, đường cao SH = h. Cho mặt phẳng (P) qua BD và vuông góc với mặt phẳng (SCD). Tính tỉ lện thể tích hai khối đa diện được chia bởi với là góc giữa hai mặt bên và mặt đáy Giải: + Gọi M, N lần lượt là trung điểm của AD và BC. + Dựng DESC. Ta có: + Gọi V =VS.ABCD, V1 = VC.EBD , V2 là phần còn lại. Xét : Ta có: (BDE)SC Suy ra: Bài 8: Cho (P) có chứa hình chữ nhật ABCD với AB = a, BC = b. Trên đường thẳng vuông góc với mặt phẳng (ABCD) tại trung điểm O của AB lấy điểm S sao cho SO = ab. Trên BC lấy BM = x, trên CD lấy DN = y Tìm mối quan hệ giữa x, y, a, b sao cho: 2) P là trung điểm của SM, Q là trung điểm của ON. Tìm điều kiện để PQ = d(SM, ON) Giải: 1) a. Giả sử ta có : . Dựng NM’SM (M’ SM). Ta có : Mặt khác: SO Do đó: MM’ Vậy để thì ta phải có (1) Ta có BM = xCM = b – x DN = yDN = a – y Vậy theo (1) ta có : Vậy điều kiện để (SOM) và (SMN) vuông góc là : b) lập luận như trên ta có điều kiện để (SON)(SMN) là ONMN Khi đó : 2) PQ = d(SM, ON) (1) Ta có : Từ (1) ta có : Vậy điều kiện để PQ là khoảng cách giữa ON và SM là : Bài 9 :Cho hình chóp S.ABCD với đáy ABCD là hình vuông cạnh a và đường cao SA = . Gọi (P) là mặt phẳng qua A và vuông góc với SC, cắt các cạnh SC, SB, SD lần lượt tại C’, B’, D’. Tính góc giữa C’D’ và AD Giải : +Gọi Dựng DKSC Mà ta cónên suy ra: đồng dạng với (1) AC’SC Từ (1) : C’E = cos SCA = + cos ADK Bài 10: Cho hình chóp S.ABCD với ABCD là hình thoi cạnh a có . Gọi O là giao điểm của AC và BD , biết SO (ABCD) và SO = . a. Xác định và tính khoảng cách giữa SB, AD. b. Tính góc giữa (SBC) và (SAD). Giải : a. Qua O dựng đường thẳng d AD và cắt AD, BC lần lượt tại I,J. + Dựng IH SJ () AD // BC Vậy IH = d(AD,SB) Dễ thấy OI = OJ =. Dựng F là hình chiếu của O trên SJ , ta dễ dàng suy ra được : OF = Suy ra : IH = 2.OF = b. Qua S dựng đường thẳng d // AD // BC, d = Ta dễ dàng có được: IJ = 2.OI = đều Vậy góc giữa (SAD) và (SBC) là Nhận xét : Ở bài toán này, để tính độ dài khoảng cách giữa hai đoạn AD và SB ta còn có thể làm như sau : + đều cạnh a SO Suy ra : VS.ABD = (1) + Mặt khác : VS.ABD = Trong đó: SB = SC = AD // BC Suy ra: VS.ABD = (2) + Từ (1) và (2) ta suy ra được : d(AD,SB) = Bài toán không khó, nó chỉ xoay quanh những phạm vi kiến thức cơ bản và chỉ đòi hỏi mức độ nắm vững kiến thức của chúng ta và sự linh hoạt trong việc biến đổi biểu thức Bài 11: Cho hình chóp S.ABC, đáy là tam giác vuông tại A. AB = a, BC = 2a. Dựng SH vuông góc với (ABC) tại H sao cho . Gọi I, J lần lượt là trung điểm của BC, SA. Gọi là mặt phẳng qua BJ và vuông góc với mặt phẳng (SHI). Tính góc giữa và (ABC). Giải: + Dễ thấy CA = a và Gọi K là trung điểm của AH Suy ra : AK (1) + Gọi N là trung điểm của SI. Áp dụng định lý Menelaus cho tam giác ICS và ba điểm B, N, M ta có : Gọi T là giao điểm của MJ và AC. Áp dụng định lí Menelaus cho tam giác ACS và ba điểm T, M, J ta có : Do đó: A là trung điểm của TC. Suy ra :BTC cân tại T . (2) Từ (1) và (2) ta có : (3) + Mặt khác , ta thấy H là hình chiếu của S trên (ABC) , do đó AH là hình chiếu của SA trên (ABC) . Mà J, K lần lượt là trung điểm cùa SA và AH. Nên K là hình chiếu của J trên (ABC) (4) + Từ (3) và (4) ta được : (JBK) TB Ta dễ dàng tính được : cos JBK = Bài 12 : Cho hình chóp C. ABB’A’ với đáy ABB’A’ là hình chữ nhật . Biết AA’ và BB’ cùng vuông góc với (ABC), dựng đường vuông góc chung của A’B và B’C. Giải : Trong mặt phẳng (ABB’A’) kẻ đường thẳng qua B’, song song với A’B và cắt AB tại D. Từ B kẻ BKCD (). Từ B kẻ BHB’K (). Từ H kẻ đường thẳng song song với A’B và cắt CB’ tại J. Từ J kẻ đường thẳng song song với BH và cắt A’B tại I Ta có : Mà DB’ // A’B nên BH A’B Mặt khác IJ // BH nên Vậy IJ là đường vuông góc chung mà ta cần dựng. Bài 13 : Cho hình chóp S.ABCD có đáy ABCD là nửa hình lục giác đều cạnh a, đường cao SA = a. Dựng đường vuông góc chung của BD, SC ; xác định chân đường vuông góc trên các cạnh SC và BD.Tính độ dài đoạn vuông góc chung đó. Giải : Qua C kẻ đường thẳng song song với BD và cắt AB và AD lần lượt tại K và E. Kẻ BHSK . Từ H kẻ đường thẳng song song với BD cắt SC tại J, từ J kẻ đường thẳng song song với BH và cắt BD tại I. + Do ABCD là nửa hình lục giác đều cạnh a nên BDAB + + Vậy IJ là đường vuông góc chung của SC và BD. Dễ thấy : Lại có tứ giác SABH nội tiếp. Do đó KH.KS = KB.KA Vậy Suy ra : (do HJ // KC). Điểm J được xác định trên CS Ta lại có: Vì BI = HJ nên . Điểm I được xác định trên BD +Ta có: ( BH // IJ , HJ // BI HJIB là hình bình hành ) BÀI TẬP TỰ LUYỆN BT1/ Cho hình chóp S.ABCD có đáy là hình vuông, mp(SAB)mp(ABCD), tam giác SAB đều. Tính góc giữa các cặp mặt phẳng sau: a/ (SAB) và (SAD); b/ (SAD) và (SBC); c/ (SHC) và (SDI), với H, I lần lượt là trung điểm của AB và BC. BT2/ Cho tứ diện ABCD, hai mp(SAB) và (SBC) vuông góc với nhau, SA vuông góc mp(ABC). Cho. Xác định để mp(SCA) và mp(SCB) tạo với nhau góc 600. BT3/ Trong mặt phẳng (P), cho hình thoi ABCD cạnh a, . Trên đường thẳng vuông góc với (P) tại giao điểm O của hai đường chéo hình thoi, lấy điểm S sao cho SO = a. Chứng minh rằng mp(SAB) vuông góc với mp(SAD). BT4/ Trong mp(P) cho hình thang cân ABCD có AB=2a, CD=a, BC=AD=a. Trên đường thẳng vuông góc với (P) tại trung điểm M của AB, lấy S: SM=a. a/ Tính bán kính mặt cầu ngoại tiếp hình chóp S.ABCD. b/ Tính góc g ... ) và trên đường trung trực của SA vẽ mp(SAH). Tứ giác AHOJ nội tiếp( J là trung điểm của SA), Do đó: Nhưng: Suy ra: R = . Tính r: Tâm O’ hình cầu nội tiếp tứ diện nằmg trên SH và trên phân giác trong của SIH( I là trung điểm của BC), góc phẳng của nhị diện cạnh BC. Tính chất của phân giác cho: Cho nên ra được tính bởi Định h để r/R lớn nhất Ta có: Đặt: Do đó: Bảng biến thiên Vậy : nếu và chỉ nếu x = 3a . x f’(x) f(x) - -a a 3a +x + + _ 0 0 Bài 2: cho hình chóp tam giác SABC. Gọi K và N là trung điểm của SA, BC. Điểm M nằm trên SC sao cho: Tìm tỉ số diện tích hai tam giác ASC và AKM. Mặt phẳng qua K song song với AB và SC có qua N không? Qua K, M, N dựng mặt phẳng mp(P). xác định tiết diện tạp bởi mp(P) với hình chóp đã cho. Chứng minh KN chia tiết diện thành 2 phần diện tích bằng nhau. Biết khoảng cách từ A đến mp(P) bằng h và thể tích hình chóp là V. tính diện tích tiết diện. Giải: Tính .AMS và SAC có cùng đường cao phát xuất từ A nên: . AMS và AMK có cùng đường cao phát xuất từ M nên: Suy ra : 2. Mặt phẳng qua K song song với AB và SC có qua N không? Mặt phẳng qua K song song với aB và SC cắt BC ở N’. Định lý Talét trong không gian cho: N là trung điểm của BC NN’ Vậy mặt phẳng qua K song song với AB và SC qua trung điểm N của BC. a. Cách dựng thiết diện: - Đường thẳng MK và đường thẳng CA cắt nhau ở I - Hai đường thẳng IN và AB cắt nhau ở H. S M K I O C N B H A Tiết diện của mặt phẳng (KMN) với hình chóp là tứ giác KMNH. b. Chứng minh Gọi O là giao điểm của MH và KN. Vẫn theo định lý Talét trong không gian ta suy ra: O là trung điểm của MH. Từ đó suy ra các đường cao MM’ và HH’ trong 2 tam giác MKN và HKN bằng nhau, do đó: Tính diện tích thiết diện: . Ta tính thể tích tứ diện AKMN bằng cách coi đáy là KMN và đỉnh là A: (1) . Cũng tứ diện ấy mà ta coi đáy là AKM và chiều cao là khoảng cách từ N đến (AKM) thì thể tích của nó là: Nếu gọi chiều cao kẻ từ B của tứ diện ABCD là hB thì ta có : Và do câu 1. ta có: (2) Từ (1) và (2) suy ra: Bài 3: Cho tứ diện SABC có các góc phẳng ở đỉnh S vuông. 1. Chứng minh : Cho biết SA = a, SB+ SC = k. đặt SB = x. tính thể tích tứ diện SABC theo a, k,x. xác định SB, SC để thể tích tứ diện SABC lớn nhất. Cho A cố định; B và C thay đổi ao cho SB + SC = k không đổi. Tìm quỹ tích điểm O của các đường chéo hình hộp có 3 cạnh là SA, SB, SC. Giải: 1 Chứng minh : . Trước hết ta chứng minh hệ thức : (1) C S B I A Vẽ SI vuông góc với AB. Theo định lý 3 đường thẳng vuông góc ta có: Áp dụng bất đẳng thức Schwarz: (1) Áp dụng kết quả (1) ta có: A S B O’ O C D 2. Tính V của tứ diện SABC . Định SB, SC để V lớn nhất. . Bất đẳng thức Cauchy: ( k, a: không đổi; x: thay đổi) Do đó : Đẳng thức xãy ra khi và chỉ khi : x = k – x Vậy xãy ra khi và chỉ khi SB = SC = Quỹ tích điểm O . Gọi O là giao điểm của các đường chéo trong hình hộp vẽ trên 3 cạnh SA, SB, SC. Nếu ta vẽ hình chữ nhật SBDC thì O chính là trung điểm của AD. Hình chiếu O’ lên mặt phẳng (SBDC) là trung điểm SD. .Chọn tia Sx mang bởi SB, định hướng từ S đến B. tia Sy mang bởi SC, định hướng từ S tới C. trong 1 phần tư mặt phẳng tọa độ Sxy ta có: J I J’ I’ S J A y x Suy ra quỹ tích của O’ là đoạn thẳng I’J’ có phương trình là: Với 2 điểm đầu là I’(k/2;0) và J’(0;k/2). . Gọi là trung điểm của SA; là điểm cố định. Ta có: Suy ra quỹ tích của O là đoạn IJ, hình biến đổi của I’J’ qua phép tịnh tiến véctơ . Bài 4: Trong 1 tứ diện chỉ có 1 cạnh có độ dài lớn hơn 1. CMR: thể tích tứ diện ấy không vựơt quá 1/8. D B F E A C H Giải: . Cho tứ diện ABCD có AB > 1 còn các cạnh khác nhỏ hơn hay bằng 1. Ta chứng minh . . Vẽ đường cao AE trong tam giác ABC và đường cao BF trong tam giác BCD. Gọi AH là đường cao của tứ diện vẽ từ A. đặt CD = a (). Ta chứng minh : .Nếu thì: ( do ) .Nếu thì: Trong cả 2 trường hợp ta đều có: Tương tự như vậy ta cũng chứng minh được: .Thể tích tứ diện: Xét hàm f(a) = f’(a) = -3a2 + 4 Bảng biến thiên: a f’(a) f (a) 0 0 0 + 1 3 0 Vậy xãy ra khi và chỉ khi a = 1. .Cuối cùng ta thử xem có tồn tại 1 tứ diện như trên không. Chọn tứ diện A D C B ABCD như sau: đều cạnh a = 1 đều cạnh a = 1 (BCD)(ACD) Ta có: ; tứ diện ABCD thỏa đề bài. Bài 5: Cho tam giác ABC đều cạnh a. một đường thẳng () tùy ý qua tâm O của tam giác cắt BC, CA, AB lần lượt tại M, N, P. Chứng minh: Cho tứ diện đều SABC. Qua đường cáo SH của tứ diện ta kẻ 1 mặt phẳng cắt các mặt bên theo những đường thẳng taọ với đáy của tứ diện các góc . Chứng minh : . Giải: 1. Chứng minh: Gọi A’, B’, C’ là trung điểm của BC, CA, AB. Đặt Ta có: Và Ta có: () A B C M< P B’ A’ C’ Cho nên 2. Chứng minh: Mặt phẳng qua SH cắt các mặt (SBC), (SAC), (SAB) theo các giao tuyến lần lượt là SM, SN và SP. Ta có: Ta có : Ta nhắc lại rằng A S B C N H P M Và theo câu 1: Cho nên : Bài 7: cho hình chóp S.ABCD có đáy là hình vuông cạnh a. cạnh bên SA vuông góc với mặt đáy. Từ A hạ các đường vuông góc AE với SB và AF với SD. Chứng minh: (AEF)SC. Goi P là giao điểm của (AEF) với SC. Tìm quỹ tích của P khi S chạt trên nửa đường thẳng Ax vuông góc với đáy ABCD. Chứng tỏ rằng có 2 vị trí của S trên Ax sao cho bằng 1 giá trị V cho Trước với điều kiện không vượt quá 1 giá trị V, nào đó mà ta phải xác định. Trong trường hợp = V1, hãy tính . Giải: Chứng minh (AEF)SC. Theo giả thiết , như vậy : D C A B F PZZZZZZZ E S Tương tự ta cũng có : Vậy 2. Quỹ tích của P. * Mặt phẳng (SAC) cố định,và AC cố định nên P ở trên đường tròn đường kính AC trong mặt phẳng (ASC). * S chỉ chạy trên nửa đường thẳng Ax nên P chỉ chạy trên nửa đường tròn nói trên, không kể điểm C. Nữa đường tròn này vẽ trong nữa ,mặt phẳng Ax giới hạn bởi AC. 3. Chứng minh có 2 vị trí của S trên Ax khi = V và V V 1. H O A S P C x h y Vẽ , PH là đường cao của hình chóp P.ABCD : PH = h. Ta có : Nếu thì ta có 2 vị trí của P trên nữa đường tròn đường kính AC, do đó có 2 vị trí của S trên Ax. Nhưng : Vậy có thể nói là : khi thì có 2 vị trí cảu S trên Ax để 4.Trong trường hợp hãy tính Theo trên ta có : ( tức P là trung điểm của cung AC) Lúc ấy P là trung điểm của SC và : Ta có : Vậy: Bài 8: Trong mặt phẳng (P) cho vuông tại B, có cạnh AB, ; và vuông tại D có AD = b ( B và D không cùng phía đối với AB). Trên đường thẳng vuông góc với mặt phẳng (P) tại A ta lấy điểm S sao cho SA = x. tính thể tích hình chóp SABCD AI, AJ, AH là 3 đường cao xuất phát từ A của 3 tam giác SAB, SAC, SAD. Hãy tìm tâm và bán kính của hình cầu ngoại tiếp các đa diện ABCIJ, ASIJH. Từ đó xác định giao của 2 hình cầu nói trê gọi là góc phẳng của nhị diện tạo bởi (SAC) và (SBC). Chứng minh : 4. phải thỏa mãn điều kiện gì để = 600. C B A D J S I H Giải: 1. tính Ta tính các chi tiết : Do đó: Do đó : Tóm lại : tâm và bán kính hình cầu ngoại tiếp các đa diện ABCIJ và ASIJH . Ta có Nên : Như vậy : I, J và B cùng nhìn AC dưới góc vuông nên hình cầu ngoại tiếp đa diện ABCIJ là hình cầu đường kính AC. Tâm là điểm giữa cả AC, bán kính bằng . I, J, H cùng nhìn AS dưới góc vuông nên hinìh cầu ngoại tiếp khối đa diện ASIJH là hình cầu đường kính AS. Tâm là điểm giữa của AS, bán kính bằng Giao của 2 hình cầu Hai hình cầu ấy có chung 3 điểm là A, I và J nên giao của chúng là đường tròn qua 3 điểm ấy. Nhưng ta đã biết nên Vậy giao của 2 hình cầu ấy là đường tròn đường kính AJ ở trong mặt phẳng qua A và vuông góc với SC. 3. Chứng minh hệ thức Góc phẳng của nhị diện tạo bởi (SAC) và (SBC) là vuông ở I : Do đó : (i) Nhưng : Thay các kết quả trên vào (i): Ta có : Vậy: 4. thỏa mãn điều kiện gì để Với thì thỏa mãn phương trình : Vậy : tam giác ABC vuông cân ở B. Bài 9: trong mặt phẳng () cho OAB và 1 điểm di động M trên đoạn AB. Từ M ta dựng đường thẳng song song với OB và OA, lần lượt cắt OA, OB tại P và Q; goil I là giao điểm của AQ và BP. Trên đường thẳng vuông góc với mp() tại M ta lấy điểm SM. Đặt OA = a, OB = b. 1. chứng minh : Từ đó suy ra thể tích của 2 hình chóp SOPIQ và SIAB bằng nhau. 2. Cho , a = 2b và . Gọi lần lượt là góc phẳng của 2 nhị diện tạo bởi (SOA) và (SOB) với mp(). Chứng minh rằng khi M di động trên đoạn AB (nhưng không trùng với A và B) thì ta luôn luôn có hệ thức: Giải: Chứng minh : S B M Q C A P I Định lý Talét : Do đó: (1) Chứng minh Để chứng minh 2 hình chóp SOPIQ và SIAB có cùng thể tích ta chỉ cần chứng minh Từ (1) ta suy ra : Từ đó : Hay : S S M H O B S S Do đó : 2. Chứng minh hệ thức: * Do OA = 2OB và nên tam giác OAB vuông tại B và là nửa tam giác đều. Và : Góc của (SOB) và mp()(OAB) là : Vẽ MHOA. Do định lý 3 đường thẳng vuông góc ta có SHOA nên góc của (SOA) với mp() là: Ta có: Từ AB = AM + MB và từ các kết quả trên ta có : . Phương pháp tọa độ: Bài 6: cho hình chóp SABC, đáy là tam giác vuông cân đỉnh C; CA = CB = a; đỉnh S có hình chiếu trên đáy là trọng tâm G cảu tam giác ABC; SG = h. Tính góc phẳng của nhị diện canh SC của hình chóp. Giải: B C A G S y a x a h z Lập hệ trục tọa độ góc Axyx, có Ax // CB, chiều dương từ C đến B; Ay chứa AC, chiều dương từ A đến C; Az có chiều dương từ G đến S. Các điểm A, B, C có tọa độ là : A(0, 0, 0); B(a, a, 0); C(a, 0, 0); S(,, h) Các vectơ có tọa độ là : Ta có: , theo thứ tự là các vectơ pháp tuyến của các mặt (SCB) và (SCA), Do đó nếu gọi là góc phẳng nhị diện cạnh SC thì : Vậy: Bài ..: cho hình chóp tứ giác đều SABCD, cạnh đáy bằng 2a, mỗi cạnh bên lập với mặt phẳng đáy 1 góc . Trong hình chóp đó, vẽ nội tiếp 1 hình lập phương sao cho các đỉnh nằm trên các trung đoạn của hình chóp. Tính độ dài cạnh cảu hình lập phương. Giải: Chọn hệ trục tọa độ Oxyz với SOz và khi đó: A D B C O M N x y S z N1 M1 E1 A(a, a, 0) , B(-a, a, 0) , C(-a, -a, 0) , D(a, -a, 0), và từ giả thiết nên S(0, 0, ). Khi đó gọi M, N theo thứ tự là trung điểm của AB, AD ta được: M(0, a, 0) , N(a, 0, 0). Giả sử Cạnh của hình lập phương bằng x, ta được: Ta có điều kiện là : Bài..: Cho hình chóp đều SABCD cạnh bằng 2a. gọi d1, d2, d3, d4 theo thứ tự là khoảng cách từ điểm M bất kỳ thuộc đáy ABCD tới các mặt bên. CMR: tổng S = d1 + d2 + d3 + d4 Không phụ thuộc vào vị trí điểm M. Giải: Chọn hệ trục tọa độ Oxyz với A, C Ox , B, D Oy và S Oz. Khi đó A(a, a, 0) , B(a, -a, 0) , C(-a, -a, 0) , D( -a, a, 0) , S(0, 0, a) Điểm M (ABCD), ta được M(x, y, 0), với , khi đó : * Phương trình mặt phẳng (SAB) được cho bởi: Suy ra khoảng cách d1 được cho bởi : A x y O B D C S z *Phương trình mặt phẳng (SBC) được cho bởi: Suy ra khoảng cách d2 được cho bởi : *Phương trình mặt phẳng (SCD) được cho bởi: Suy ra khoảng cách d3 được cho bởi : *Phương trình mặt phẳng (SDA) được cho bởi: Suy ra khoảng cách d4 được cho bởi : Từ đó : S = d1 + d2 + d3 + d4 =
Tài liệu đính kèm:
 HKG HC.doc
HKG HC.doc





